Solve Optimization Problems in Python by Using SciPy Library – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In our previous post, which can be accessed here, we explained how to solve ordinary differential equations by using the SciPy library. In this post, we explain how to solve optimization problems in Python by using the SciPy Python library. We use the SciPy function minimize() to solve optimization problems. The complete code is given at the end of this post. The YouTube video accompanying this post is given below.

In order to explain how to solve optimization problems in Python, we first need to select a test problem. We need to be able to determine the solution to the test problem analytically so we can compare the analytical results with the results obtained by using the SciPy library. In this way, we can truly evaluate the performance and accuracy of the optimization problem.

As the test case, we consider the problem of computing the solution of the following system of linear equations:

(1) $\begin{align*}\mathbf{y}=A \mathbf{x}\end{align*}$

where $\mathbf{y}\in \mathbb{R}^{n}$ , $A \in \mathbb{R}^{n\times n}$ , and $\mathbf{x}\in \mathbb{R}^{n}$ . That is, $\mathbf{x}$ and $\mathbf{y}$ are n-dimensional vectors. Under the assumption that the matrix $A$ is nonsingular, the solution is given by the following equation

(2) $\begin{align*}\hat{\mathbf{x}}=A^{-1}\mathbf{y}\end{align*}$

where $A^{-1}$ denotes the matrix inverse. On the other hand, the solution of the system of linear equations (1) can be also expressed as the solution of the following least-squares optimization problem

(3) $\begin{align*}\min_{\mathbf{x}} \left\|\mathbf{y}-A\mathbf{x} \right\|_{2}^{2}\end{align*}$

where $\left\| \cdot \right\|_{2}^{2}$ denotes the vector 2-norm. As we have explained in our previous post, whose link is given here, the solution to the least squares problem is given by

(4) $\begin{align*}\hat{\mathbf{x}}_{LS}=(A^{T}A)^{-1}A^{T}\mathbf{y}\end{align*}$

Now, by using this rule $(BC)^{-1}=C^{-1}B^{-1}$ , where $B$ and $C$ are two square invertible matrices, from (4), we obtain

(5) $\begin{align*}(A^{T}A)^{-1}A^{T}=A^{-1}(A^{T})^{-1}A^{T}=A^{-1}\end{align*}$

by substituting (5) in (4), we can see that the solution of the least squares problem is equivalent to the solution of the system of linear equations given by (2). Now that we constructed and analyzed the test case. Let us proceed with Python implementation.

First, we import the necessary libraries and construct the test problem consisting of the random matrix $A$ and random vector $\mathb{x}$ . That is, we first deliberately choose a random solution that we call the true solution in the code.

# -*- coding: utf-8 -*-
"""
Created on Sat Oct 15 18:02:51 2022

@author: aleks
"""

import numpy as np 
import scipy
from scipy.optimize import minimize

# define a random matrix A that is our data matrix
A=np.random.randn(10,10)

# choose the true solution
trueSolutionX=np.random.randn(10,1)
# compute the right-hand side corresponding to the true solution
trueSolutionY=np.matmul(A,trueSolutionX)

Next, we compute the analytical solution by using matrix inverse.

# computed solution
computedSolutionX=np.matmul(np.linalg.inv(A),trueSolutionY)
# right-hand side computed on the basis of the computed solution
computedSolutionY=np.matmul(A,computedSolutionX)

To quantify the accuracy, we compute the absolute errors

(6) $\begin{align*}\mathbf{e}_{\mathbf{x}}&=\mathbf{x}-\hat{\mathbf{x}} \\\mathbf{e}_{\mathbf{y}}&=\mathbf{y}-\hat{\mathbf{y}}, \;\; \hat{\mathbf{y}}=A\hat{\mathbf{x}}\end{align*}$

and relative errors

(7) $\begin{align*}\varepsilon_{\mathbf{x}}&=\frac{\left\|\mathbf{e}_{\mathbf{x}}\right\|_{2}}{\left\|\mathbf{x}\right\|_{2}} \\\varepsilon_{\mathbf{y}}&=\frac{\left\| \mathbf{e}_{\mathbf{y}}\right\|_{2}}{\left\| \mathbf{y}\right\|_{2}}\end{align*}$

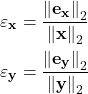
The relative errors are computed as follows

# solution error
errorSolutionX= trueSolutionX-computedSolutionX
# error in the right-hand side
errorPredictionY=trueSolutionY-computedSolutionY

# relative error
np.linalg.norm(errorSolutionX,2)/np.linalg.norm(trueSolutionX,2)
np.linalg.norm(errorPredictionY,2)/np.linalg.norm(trueSolutionY,2)

To use the SciPy function minimize(), we first need to define the cost function that is originally given by (3). For a given value of $\mathbf{x}$ , and for given values of the matrix $A$ and the vector $\mathbf{y}$ , this function should return the value of the cost function that is given by

(8) $\begin{align*} \left\|\mathbf{y}-A\mathbf{x} \right\|_{2}^{2}\end{align*}$

This cost function can be formulated as the following function in Python:

# define the cost function
def costFunction(x,Amatrix, Yvector):
    error=Yvector-np.matmul(Amatrix,x)
    returnValue=np.linalg.norm(error,2)**2
    return returnValue

The SciPy function minimize() uses iterative methods to solve optimization problems. Consequently, we need to specify an initial guess of the solution. We use a random value of the initial guess:

# select the initial guess
initialGuess=np.random.randn(10)

In this post, we use the Nelder-Mead method for solving the optimization problem. To properly use this method, we need to specify several parameters. The possible values of the parameters can be found by executing this code line in Python

# see all the options for the solver
scipy.optimize.show_options(solver='minimize',method='nelder-mead')

The output is

Minimization of scalar function of one or more variables using the
Nelder-Mead algorithm.

Options
-------
disp : bool
    Set to True to print convergence messages.
maxiter, maxfev : int
    Maximum allowed number of iterations and function evaluations.
    Will default to ``N*200``, where ``N`` is the number of
    variables, if neither `maxiter` or `maxfev` is set. If both
    `maxiter` and `maxfev` are set, minimization will stop at the
    first reached.
return_all : bool, optional
    Set to True to return a list of the best solution at each of the
    iterations.
initial_simplex : array_like of shape (N + 1, N)
    Initial simplex. If given, overrides `x0`.
    ``initial_simplex[j,:]`` should contain the coordinates of
    the jth vertex of the ``N+1`` vertices in the simplex, where
    ``N`` is the dimension.
xatol : float, optional
    Absolute error in xopt between iterations that is acceptable for
    convergence.
fatol : number, optional
    Absolute error in func(xopt) between iterations that is acceptable for
    convergence.
adaptive : bool, optional
    Adapt algorithm parameters to dimensionality of problem. Useful for
    high-dimensional minimization [1]_.
bounds : sequence or `Bounds`, optional
    Bounds on variables. There are two ways to specify the bounds:

        1. Instance of `Bounds` class.
        2. Sequence of ``(min, max)`` pairs for each element in `x`. None
           is used to specify no bound.

    Note that this just clips all vertices in simplex based on
    the bounds.

For us the most important parameters are given by the following dictionary:

options={'maxiter': 10000,'maxfev':10000,'xatol': 1e-8, 'disp': True}

They are the maximum number of iterations, given by “maxiter”, maximum number of function evaluations, given by “maxfev”, solution tolerance, given by “xatol”, and display parameter (controlling the display output), given by “disp”. This dictionary is directly used in the minimization function. The solution is computed by using the minimize() function:

# compute the solution
result = minimize(costFunction, initialGuess, method='nelder-mead',
               args=(A, np.reshape(trueSolutionY,(10,))), options={'maxiter': 10000,'maxfev':10000,'xatol': 1e-8, 'disp': True})

The first argument of the minimize() function is the name of the cost function. In our case, the name of the previously defined cost function is “costFunction”. The second argument is the initial guess of the solution. The third argument is the name of the solution method. The fourth argument contains additional parameters or arguments that are sent to the cost function (matrix A and initial guess of the solution). The last argument is the dictionary containing the solution options. This function returns a structure called “result” that looks like this

final_simplex: (array([[ 0.50927902,  0.07721123,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873607, -0.18672033, -1.27336894,  2.55132424],
       [ 0.50927903,  0.07721123,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873607, -0.18672033, -1.27336894,  2.55132424],
       [ 0.50927903,  0.07721123,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873607, -0.18672033, -1.27336894,  2.55132424],
       [ 0.50927903,  0.07721123,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873607, -0.18672033, -1.27336894,  2.55132424],
       [ 0.50927902,  0.07721124,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873608, -0.18672034, -1.27336894,  2.55132425],
       [ 0.50927902,  0.07721124,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873608, -0.18672033, -1.27336894,  2.55132425],
       [ 0.50927903,  0.07721123,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873607, -0.18672033, -1.27336894,  2.55132424],
       [ 0.50927903,  0.07721123,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873607, -0.18672033, -1.27336894,  2.55132424],
       [ 0.50927903,  0.07721123,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873607, -0.18672033, -1.27336894,  2.55132424],
       [ 0.50927903,  0.07721123,  1.35498508,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873607, -0.18672033, -1.27336894,  2.55132424],
       [ 0.50927902,  0.07721124,  1.35498507,  2.29627946,  2.29458652,
        -1.6091885 ,  0.83873608, -0.18672034, -1.27336894,  2.55132425]]), array([1.57894307e-17, 1.63964136e-17, 1.69029725e-17, 1.80542101e-17,
       1.81308128e-17, 1.84480734e-17, 2.31529854e-17, 2.35944743e-17,
       2.49032925e-17, 2.54938476e-17, 2.68033672e-17]))
           fun: 1.5789430742143885e-17
       message: 'Optimization terminated successfully.'
          nfev: 6831
           nit: 4837
        status: 0
       success: True
             x: array([ 0.50927902,  0.07721123,  1.35498508,  2.29627946,  2.29458652,
       -1.6091885 ,  0.83873607, -0.18672033, -1.27336894,  2.55132424])

The solution can be accessed by typing in Python:

# retrieve the solution
computedSolutionOptimizationX=result.x

Next, we compute the vector $\mathbf{y}$ on the basis of the computed solution, and we compute the errors

# computed the right-hand side for the optimization solution
computedSolutionOptimizationY=np.matmul(A,computedSolutionOptimizationX)
# solution error
errorSolutionOptimizationX= np.reshape(trueSolutionX,(10,))-computedSolutionOptimizationX
# error in the right-hand side
errorPredictionOptimizationY=np.reshape(trueSolutionY,(10,))-computedSolutionOptimizationY
# relative error
np.linalg.norm(errorSolutionOptimizationX,2)/np.linalg.norm(trueSolutionX,2)
np.linalg.norm(errorPredictionOptimizationY,2)/np.linalg.norm(trueSolutionY,2)

Tha is all. In this post, we learned how to solve optimization problems in Python by using SciPy function minimize(). The complete code is given below.

# -*- coding: utf-8 -*-
"""
Created on Sat Oct 15 18:02:51 2022

@author: aleks
"""

import numpy as np 
import scipy
from scipy.optimize import minimize

# define a random matrix A that is our data matrix
A=np.random.randn(10,10)

# choose the true solution
trueSolutionX=np.random.randn(10,1)
# compute the right-hand side corresponding to the true solution
trueSolutionY=np.matmul(A,trueSolutionX)

# computed solution
computedSolutionX=np.matmul(np.linalg.inv(A),trueSolutionY)
# right-hand side computed on the basis of the computed solution
computedSolutionY=np.matmul(A,computedSolutionX)

# solution error
errorSolutionX= trueSolutionX-computedSolutionX
# error in the right-hand side
errorPredictionY=trueSolutionY-computedSolutionY

# relative error
np.linalg.norm(errorSolutionX,2)/np.linalg.norm(trueSolutionX,2)
np.linalg.norm(errorPredictionY,2)/np.linalg.norm(trueSolutionY,2)

## Now, we solve the problem by using an optimization approach

# define the cost function
def costFunction(x,Amatrix, Yvector):
    error=Yvector-np.matmul(Amatrix,x)
    returnValue=np.linalg.norm(error,2)**2
    return returnValue


# select the initial guess
initialGuess=np.random.randn(10)


# see all the options for the solver
scipy.optimize.show_options(solver='minimize',method='nelder-mead')

# compute the solution
result = minimize(costFunction, initialGuess, method='nelder-mead',
               args=(A, np.reshape(trueSolutionY,(10,))), options={'maxiter': 10000,'maxfev':10000,'xatol': 1e-8, 'disp': True})

# retrieve the solution
computedSolutionOptimizationX=result.x

# computed the right-hand side for the optimization solution
computedSolutionOptimizationY=np.matmul(A,computedSolutionOptimizationX)


# solution error
errorSolutionOptimizationX= np.reshape(trueSolutionX,(10,))-computedSolutionOptimizationX
# error in the right-hand side
errorPredictionOptimizationY=np.reshape(trueSolutionY,(10,))-computedSolutionOptimizationY

# relative error
np.linalg.norm(errorSolutionOptimizationX,2)/np.linalg.norm(trueSolutionX,2)
np.linalg.norm(errorPredictionOptimizationY,2)/np.linalg.norm(trueSolutionY,2)

admin

You might also like

Clear and Concise Explanation of the Law of Sines With Solved Examples

Interpolation of Function Values in MATLAB

ENS100- Exam