In this tutorial, we provide a brief introduction to open-loop observers. In this tutorial, you will learn
- The concept of observability.
- How to estimate an initial state of a linear dynamical system by using an open-loop observer.
- How to properly understand the concept of numerical observability.
The motivation for creating this tutorial comes from the fact that students often have difficulties understanding the concept of observability and they often do not understand the need for observers. This comes from the fact that the concept of observability is often first taught by assuming continuous-time systems. The mathematics needed to describe continuous-time systems is more complex than the mathematics necessary to describe discrete-time systems. It involves integrals applied to vector and matrix expressions that often involve matrix exponentials. These concepts might be difficult to understand for an average engineering student.
Instead of introducing the concept of observability by assuming a continuous-time system, we will present this concept by assuming a discrete-time system. In this way, we significantly simplify the mathematics necessary to understand the basic concepts.
So let us immediately explain the need for observability analysis by considering the example shown in the figure below.
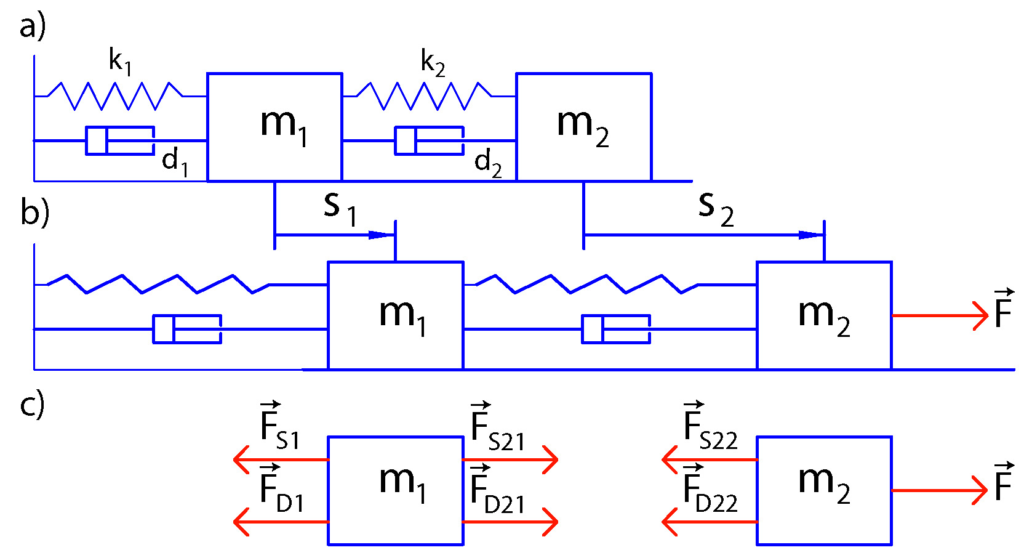
The above figure illustrates a prototypical model of two masses connected with springs and dampers. There is a force ![]() moving the second mass. The equations governing the behavior of this system are very similar to the equations of motion of a number of mechanical and electrical systems, such as electrical and electronics circuits, mechanical systems whose motion is described by Newton’s equations, robotic arms, etc.
moving the second mass. The equations governing the behavior of this system are very similar to the equations of motion of a number of mechanical and electrical systems, such as electrical and electronics circuits, mechanical systems whose motion is described by Newton’s equations, robotic arms, etc.
In our previous post, whose link is given here, we have derived a state-space model of this system. The states are:
(1) 
In order to develop a feedback control it is often necessary to obtain information about all the states: ![]() and
and ![]() . However, in practice, we can only observe a single state variable, such as, for example, position
. However, in practice, we can only observe a single state variable, such as, for example, position ![]() or
or ![]() . The observability analysis tries to provide the answers to these types of questions
. The observability analysis tries to provide the answers to these types of questions
- Is it possible to reconstruct the full state vector (all state variables
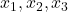 and
and 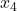 ) by only measuring the position of the first mass over time? That is, is it possible to reconstruct time series
) by only measuring the position of the first mass over time? That is, is it possible to reconstruct time series 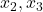 and
and 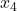 by only observing the time series of
by only observing the time series of 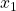 ?
? - If it is not possible to reconstruct all other state variables by only measuring
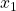 , then how many state variables do we need to observe to reconstruct the full state vector?
, then how many state variables do we need to observe to reconstruct the full state vector?
Consider the following linear discrete-time system
(2) ![]()
where ![]() is the system state at the discrete-time sample
is the system state at the discrete-time sample ![]() ,
, ![]() is the output of the system at the discrete-time sample
is the output of the system at the discrete-time sample ![]() , and
, and ![]() and
and ![]() are system matrices. The system output
are system matrices. The system output ![]() is usually observed by a sensor. However, the state of the system
is usually observed by a sensor. However, the state of the system ![]() is usually not directly observable.
is usually not directly observable.
Note that we have assumed that the inputs are not affecting our system dynamics. This is done for presentation clarity since the inputs do not affect the system observability. We can also easily modify our approach to include the system’s inputs.
Let us consider the following problem. Our task is to estimate the system’s initial state ![]() , (the system state
, (the system state ![]() at the discrete-time sample
at the discrete-time sample ![]() ), from the sequence of the observed outputs
), from the sequence of the observed outputs ![]() , where
, where ![]() is the total number of outputs (observations). This problem is in fact the observability problem for the discrete time system (2)
is the total number of outputs (observations). This problem is in fact the observability problem for the discrete time system (2)
So how to mathematically formulate and solve this problem?
By propagating the state equation of the system (2) in discrete-time, we have
(3) 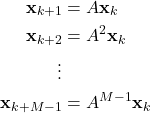
Combining these equations with the output equation, we obtain
(4) 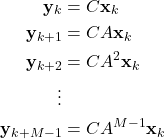
These equations can be written in the vector-matrix form
(5) 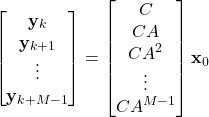
The last equation can be written compactly
(6) ![]()
where
(7) 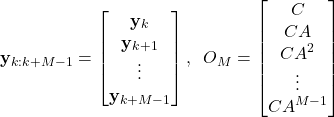
When ![]() , where
, where ![]() is the state order of the system, the matrix
is the state order of the system, the matrix ![]() (matrix
(matrix ![]() for M=n) is called the observability matrix.
for M=n) is called the observability matrix.
The notation ![]() denotes the lifted vector. Lifted vectors are formed by “lifting” underlying vectors over time. This means that the vector
denotes the lifted vector. Lifted vectors are formed by “lifting” underlying vectors over time. This means that the vector ![]() is formed by stacking vectors
is formed by stacking vectors ![]() ,
, ![]() ,
, ![]() ,
, ![]() on top of each other. The subscript notation
on top of each other. The subscript notation ![]() , means that the starting time instant for lifting is
, means that the starting time instant for lifting is ![]() and the ending time instant is
and the ending time instant is ![]() . By setting
. By setting ![]() in (6), we obtain
in (6), we obtain
(8) ![]()
The last equation is important since it shows us that the observability problem is to determine the initial state ![]() from the observation vector
from the observation vector ![]() . Since the last equation represents a system of linear equations, the observability problem is equivalent to the problem of solving the system of linear equations, where the unknown variables are entries of the vector
. Since the last equation represents a system of linear equations, the observability problem is equivalent to the problem of solving the system of linear equations, where the unknown variables are entries of the vector ![]() . In order to ensure that this system has a unique solution, or equivalently in order to ensure that the system is observable, in the most general case, it is necessary and sufficient that:
. In order to ensure that this system has a unique solution, or equivalently in order to ensure that the system is observable, in the most general case, it is necessary and sufficient that:
- The number of observation samples
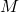 is larger than or equal to
is larger than or equal to 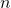 , where
, where 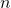 is the system state order.
is the system state order. 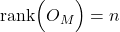 . This means that the observability matrix
. This means that the observability matrix 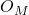 has full rank.
has full rank.
Here, a few important things should be kept in mind. Condition (1) is stated for the most general case. However, it might happen that the output dimension ![]() (the dimension of the vector
(the dimension of the vector ![]() ) is such that we can ensure that the matrix
) is such that we can ensure that the matrix ![]() has full rank even if
has full rank even if ![]() . For example, consider this system
. For example, consider this system
(9) ![]()
where ![]() is an identity matrix. In the case of this system,
is an identity matrix. In the case of this system, ![]() , will ensure the system observability since the matrix
, will ensure the system observability since the matrix ![]() is equal to the identity matrix, and identity matrices are invertible. In practice, it is not necessary to take the number of samples
is equal to the identity matrix, and identity matrices are invertible. In practice, it is not necessary to take the number of samples ![]() to be larger than
to be larger than ![]() . This is because the entries
. This is because the entries ![]() for
for ![]() can be expressed as linear combinations of CA^{P}, where
can be expressed as linear combinations of CA^{P}, where ![]() . This follows from the Cayley-Hamilton theorem. However, in the presence of the measurement noise in the equation (2), it might be beneficial to take more samples
. This follows from the Cayley-Hamilton theorem. However, in the presence of the measurement noise in the equation (2), it might be beneficial to take more samples ![]() (and
(and ![]() should be larger than
should be larger than ![]() ), since, in this way, it is possible to decrease the sensitivity of estimating the initial state from the observed outputs.
), since, in this way, it is possible to decrease the sensitivity of estimating the initial state from the observed outputs.
Let us assume that the conditions (1) and (2) are satisfied. We can multiply the equation (8) from left by ![]() , and as the result, we obtain
, and as the result, we obtain
(10) ![]()
Then, since the matrix ![]() has a full column rank, the matrix
has a full column rank, the matrix ![]() is invertible, and from (10), we obtain
is invertible, and from (10), we obtain
(11) ![]()
The equation (11) is the solution to the observability problem. We have obtained an initial state estimate as a function of the observations: ![]() .
.
Now that we have informally introduced the concept of observability, we can give a formal definition:
Observability Definition: The system (2) is observable, if any initial state ![]() is uniquely determined by the observed outputs
is uniquely determined by the observed outputs ![]() , for some finite positive integer
, for some finite positive integer ![]() .
.
We can also state the observability rank condition:
Observability rank condition: The system (2) is observable if and only if ![]() .
.
From everything being said, it follows that we can check the observability condition by investigating the rank of the matrix ![]() .
.
However, this criterion has the following issue. Namely, formally speaking, the matrix might have a full rank, however, it might be close to the singular matrix. That is, its condition number might be very large or its smallest singular value might be close to zero. This implies that in order to investigate the observability of the system it is usually more appropriate to compute the condition number or the smallest singular value.
Let us numerically illustrate all these concepts by using the example from the beginning of this post. In our previous post, explaining the subspace identification method, we have introduced this example This example is briefly summarized below. For completeness, we repeat the figure illustrating this example.

The state-space model is given below
(12) 
We assume that only the position of the first object can be directly observed. This can be achieved using for example, infrared distance sensors. Under this assumption, the output equation has the following form
(13) ![]()
The next step is to transform the state-space model (12)-(13) in the discrete-time domain. Due to its simplicity and good stability properties we use the Backward Euler method to perform the discretization. This method approximates the state derivative as follows
(14) ![]()
where ![]() is the discretization time step. For simplicity, we assumed that the discrete-time index of the input is
is the discretization time step. For simplicity, we assumed that the discrete-time index of the input is ![]() . We can also assume that the discrete-time index of input is
. We can also assume that the discrete-time index of input is ![]() . However, then, when simulating the system dynamics we will start from
. However, then, when simulating the system dynamics we will start from ![]() . From the last equation, we have
. From the last equation, we have
(15) ![]()
where ![]() and
and ![]() . On the other hand, the output equation remains unchanged
. On the other hand, the output equation remains unchanged
(16) ![]()
We neglect the input and without the loss of generality, we shift the time index from ![]() to
to ![]() , and consequently, we obtain the final state-space model
, and consequently, we obtain the final state-space model
(17) ![]()
Next, we introduce the MATLAB code. First, we define the model parameters and other variables
clear,pack,clc
% model parameters
k1=10, k2=20, d1=0.5, d2=0.3, m1=10, m2=20
% discretization constant
h=0.1
% simulate the system
simulationTime=500
% number of time steps for estimating the initial state
M=5
%% system matrices
Ac=[0 1 0 0;
-(k1+k2)/m1 -(d1+d2)/m1 k2/m1 d2/m1;
0 0 0 1;
k2/m2 d2/m2 -k2/m2 -d2/m2]
C=[1 0 0 0]
[s1,s2]=size(C)
% discrete-time system
A=inv(eye(4)-h*Ac)
% select the initial state to be estimated
x0=[0.5;0.1;0; -0.4];
First, we define the model parameters such as damping, stifness and masses. We use a discretization constant of ![]() , and total simulation time of 500. Then, we define the system matrices
, and total simulation time of 500. Then, we define the system matrices ![]() and
and ![]() , and we define the discretized matrix
, and we define the discretized matrix ![]() . We define the initial state. This state is used to simulate the system response and we will estimate this initial state. We select
. We define the initial state. This state is used to simulate the system response and we will estimate this initial state. We select ![]() time samples to form the lifted vectors and the observability matrix.
time samples to form the lifted vectors and the observability matrix.
Next, we simulate the system response. The following code lines simulate the system response and form the obeservability matrix
%% simulate the system
stateVector=zeros(4,simulationTime+1);
outputVector=zeros(s1,simulationTime+1);
stateVector(:,1)=x0;
outputVector(:,1)=C*x0;
for i=1:simulationTime
stateVector(:,i+1)=A*stateVector(:,i);
outputVector(:,i+1)=C*stateVector(:,i+1);
end
% form the M-steps observability matrix
for i=1:M
Obs{i,1}=C*A^(i-1); % M-steps observability matrix
Y{i,1}=outputVector(:,i); % Lifted output vector
end
Obs=cell2mat(Obs);
Y=cell2mat(Y);
% plot the response
simulationTimeVector=0:h:h*simulationTime;
figure(1)
plot(simulationTimeVector,outputVector,LineWidth=2)
xlabel('time')
ylabel('output')
grid
The system response is shown in the figure below.
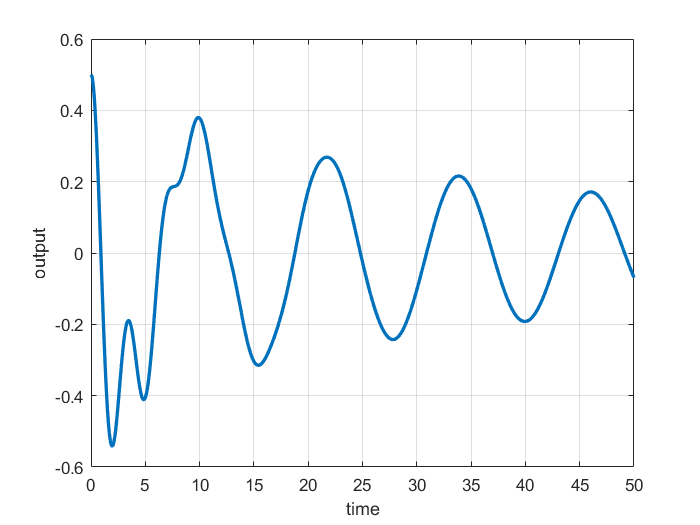
Next, we estimate the initial state by using the equation (11). Then we compare the estimate with the initial state by computing the relative estimation error. Then, we compute the singular values of the observability matrix and compute the condition number.
% estimate the initial state
x0Est=inv(Obs'*Obs)*Obs'*Y
% compute the relative error
norm(x0Est-x0,2)/norm(x0,2)
% compute the singular value decomposition
[U,S,V] = svd(Obs);
% singular values
diag(S)
% condition number
cond(Obs)
You can modify this code by changing the structure of the C matrix. For example, you can investigate the effect of observing some other variable (for example, what happens when ![]() ). This is explained in the accompanying YouTube video. Also, you can modify the number of observability steps and modify the system parameters.
). This is explained in the accompanying YouTube video. Also, you can modify the number of observability steps and modify the system parameters.
Is it possible to apply this observer in simulink?
Probably it is. However, I do not have enough time to investigate how to do this.