Pole Placement State-Space Control in Simulink Together With Integral Control to Eliminate Steady State Error – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this control system tutorial, we explain how to develop a controller by using a pole-placement method. The controller includes an integral control action to eliminate steady-state errors. We explain how to model and simulate this controller in Simulink and MATLAB. The YouTube tutorial is given below. In our next tutorial, whose link is given here, we explain how to model the Linear Quadratic Regulator (LQR) controller in Simulink.

As a test case, we consider the mass-spring-damper system shown in the figure below.

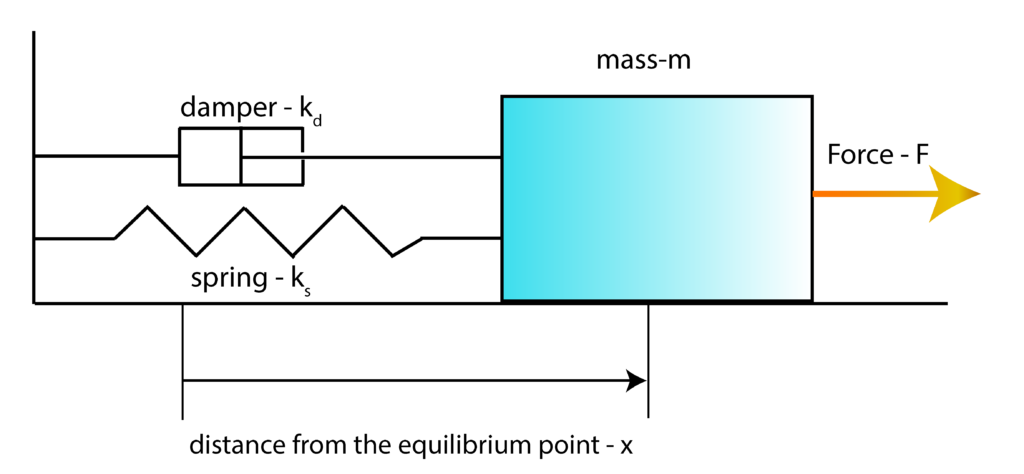
This model is thoroughly explained in our previous tutorial which can be found here. The distance from the equilibrium point is denoted by $x$ . The spring and damper constants are denoted by $k_{s}$ and $k_{d}$ . The force is denoted by $F$ and the mass of the object is denoted by $m$ . In our previous tutorial, we derived the state-space model of the system. The state-space variables are

(1) $\begin{align*}x_{1}=x \\x_{2}=\dot{x}\end{align*}$

The resulting state-space model has the following form:

(2) $\begin{align*}\dot{\mathbf{x}}& =A\mathbf{x}+B\mathbf{u} \\\mathbf{y}&=C\mathbf{x} \end{align*}$

where

(3) $\begin{align*}\mathbf{x}=\begin{bmatrix}x_{1} \\ x_{2} \end{bmatrix},\;\; A=\begin{bmatrix}0 & 1 \\ -\frac{k_{s}}{m} & -\frac{k_{d}}{m} \end{bmatrix},\;\; B=\begin{bmatrix} 0 \\ \frac{1}{m} \end{bmatrix},\;\; C=\begin{bmatrix}1 & 0 \end{bmatrix}\end{align*}$

Our goal is to design a controller that will make the output $\mathbf{y}$ of the system (2) track a constant reference signal. Let the reference signal be denoted by $\mathbf{r}$ . The reference signal is a desired output determined by the user. Let the control error (also called the tracking error), be denoted by

(4) $\begin{align*}\mathbf{e}=\mathbf{r}-\mathbf{y}\end{align*}$

Then, the goal of the controller is to decrease the control error as close as possible to zero.

The basic controller based on pole placement or Linear Quadratic Regulator (LQR) can be used to steer the system to the zero equilibrium point. That is, these controllers can be used to steer the system’s state to zero state $\mathbf{x}=0$ . However, in the most general case, they will not ensure that the error (4) will converge to zero. To ensure that the error converges to zero for a constant reference signal, we need to add an integrator to our controller.

We add an integrator by augmenting our original state-space model, with the state of the integral controller. Let us introduce a new variable $\mathbf{x}_{i}$ that is an integral of the control error. That is,

(5) $\begin{align*}\mathbf{x}_{i}=\int \big( \mathbf{e} \big) \text{d}t =\int \big(\mathbf{r} - \mathbf{y} \big) \text{d}t\end{align*}$

By taking the first derivative of (5), we obtain

(6) $\begin{align*}\dot{\mathbf{x}}_{i}=\mathbf{r} - \mathbf{y}\end{align*}$

By substituting the output equation of the state-space model (2) in (6), we obtain

(7) $\begin{align*}\dot{\mathbf{x}}_{i}=\mathbf{r} - C\mathbf{x}\end{align*}$

By combining the state equation of the model (2) with the integral controller (7), we obtain

(8) $\begin{align*}\dot{\mathbf{x}}& =A\mathbf{x}+B\mathbf{u} \\\dot{\mathbf{x}}_{i}& =\mathbf{r} - C\mathbf{x}\end{align*}$

The last two equations can be written in the compact form

(9) $\begin{align*}\begin{bmatrix} \dot{\mathbf{x}} \\ \dot{\mathbf{x}}_{i} \end{bmatrix}=\begin{bmatrix}A & 0 \\ -C & 0 \end{bmatrix}\begin{bmatrix} \mathbf{x} \\ \mathbf{x}_{i} \end{bmatrix}+\begin{bmatrix}B \\ 0 \end{bmatrix}\mathbf{u}+\begin{bmatrix}0 \\ I \end{bmatrix}\mathbf{r}\end{align*}$

The last equation can be written compactly as follows

(10) $\begin{align*}\dot{\mathbf{x}}_{a}=A_{a}\mathbf{x}_{a}+B_{a}\mathbf{u}+B_{r}\mathbf{r}\end{align*}$

where

(11) $\begin{align*}\mathbf{x}_{a}=\begin{bmatrix} \mathbf{x} \\ \mathbf{x}_{i} \end{bmatrix},\;\; A_{a}=\begin{bmatrix}A & 0 \\ -C & 0 \end{bmatrix},\;\; B_{a}=\begin{bmatrix}B \\ 0 \end{bmatrix},\;\; B_{r}=\begin{bmatrix}0 \\ I \end{bmatrix}\end{align*}$

In this tutorial, we assume that the state vector of the augmented system $\mathbf{x}_{a}$ is known. In our next tutorial, we will relax this assumption by introducing a state observer. Consequently, we can design a state-feedback controller that will place the poles of the closed-loop system in desired locations in the complex plane. For example, to place the poles at the desired locations we can use the MATLAB function “place()”. This will be explained later in the tutorial. The pole placement method designs a feedback control law:

(12) $\begin{align*}\mathbf{u}=-K\mathbf{x}_{a}\end{align*}$

By partitioning $K$ as follows

(13) $\begin{align*}K=\begin{bmatrix}K_{x} & K_{i} \end{bmatrix}\end{align*}$

and by using the definition of $\mathbf{x}_{a}$ given in (11), we obtain

(14) $\begin{align*}\mathbf{u}=-K\mathbf{x}_{a}=-\begin{bmatrix} K_{x} & K_{i} \end{bmatrix}\begin{bmatrix} \mathbf{x} \\ \mathbf{x}_{i} \end{bmatrix}=-K_{x}\mathbf{x}-K_{i} \mathbf{x}_{i} \end{align*}$

By using (5), the last equation can be written as follows

(15) $\begin{align*}\mathbf{u}=-K_{x}\mathbf{x}-K_{i} \mathbf{x}_{i} =-K_{x}\mathbf{x}-K_{i}\int \big(\mathbf{r} - \mathbf{y} \big) \text{d}t \end{align*}$

We can clearly observe that the controller explicitly takes into account the integral of the control error. To develop a Simulink model and simulate it, we need to create a block diagram of the system and the controller. The block diagram is given below.

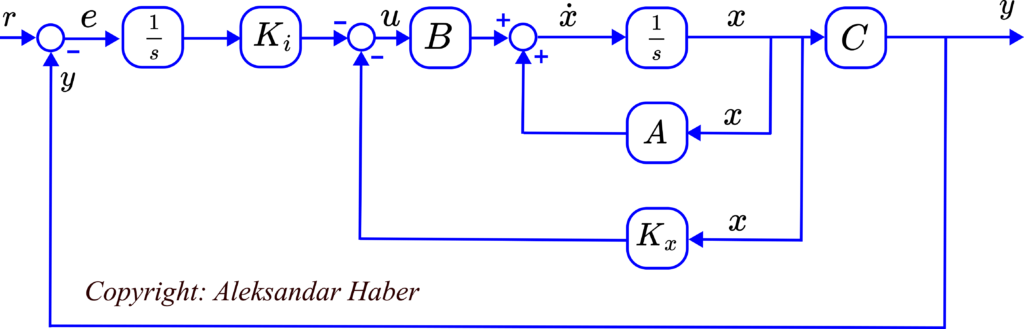
Figure 1: Block diagram of the control system that is used to model and simulate the system in Simulink.

The MATLAB code is given below.

ks=1
kd=0.1
m=10

A=[0 1; -ks/m -kd/m];
B=[0; 1/m];
C=[1 0]
D=[0]

% compute the open loop poles
openLoopPoles=eig(A)

% form the augmented system
Aa=[A [0; 0]; -C 0]
Ba=[B;0]

% set the desired closed-loop pole locations
desiredClosedPoles=[-2+0.2i; -2-0.2i;-3]

% use the place command to place the closed loop poles at the desired
% locations
K=place(Aa,Ba,desiredClosedPoles)
% check the closed loop poles
eig(Aa-Ba*K)
% extract feedback matrices

Kx=K(:,1:2)
Ki=K(3)

This code will calculate the feedback control matrix $K$ that will place the poles at the desired locations specified by the vector “desiredClosedPoles”. Then, from the calculated $K$ matrix, we can extract $K_{x}$ and $K_{i}$ . Before creating the Simulink model, it is important to run this MATLAB script such that all the necessary variables are in the MATLAB workspace and such that the Simulink model can access these variables. The Simulink modeling and simulation is explained in the YouTube tutorial video at the top of this page.

admin

You might also like

Review of the Methods of Statics

Influence of Zeros and Non-Minimum Phase Zeros of Transfer Functions on Dynamical System Behavior

Basics of Unit Conversion