In this tutorial and in the accompanying YouTube video, we derive and explain the formula for the settling time of the transient response of a dynamical system. This formula is important since it relates the settling time with the natural undamped frequency and damping ratio. Also, it can be used to design controllers that meet certain transient response specifications. The YouTube video accompanying this post is given below.
Final expression
In this post, we show that the settling time of the transient response can be approximated by the following equation
(1) ![]()
where ![]() is the settling time,
is the settling time, ![]() is the damping ratio, and
is the damping ratio, and ![]() is the natural undamped frequency.
is the natural undamped frequency.
Derivation of the formula for the settling time
The prototype second-order system has the following form:
(2) ![]()
where
 is the complex variable
is the complex variable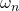 is the natural undamped frequency
is the natural undamped frequency 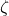 is the damping ratio
is the damping ratio
When deriving the formulas, we assume that the input of the system is a step signal. The output is then
(3) ![]()
In our previous post, which can be found here, we derived an analytical form of the step response in the time domain. The response has the following form
(4) ![]()
With this formula, it is always a good idea to give the following figure (see below) that illustrates the poles of the prototype system (2). A detailed explanation of this figure can be found in our previous post that can be found here.
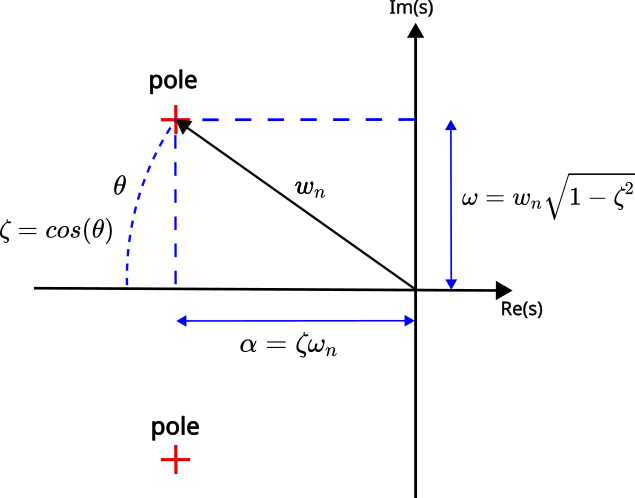
Let us now analyze the equation (4). The envelopes of the transient response are given by the following exponential functions
(5) 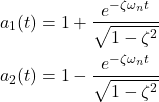
The step response of the system with the two envelopes are shown in the figure below.
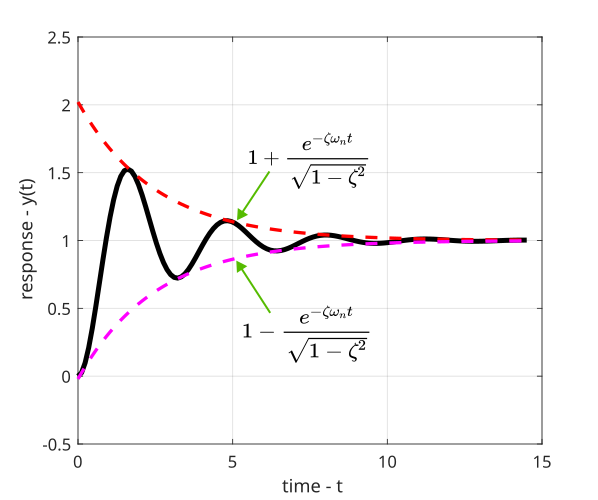
This graph is generated by using the following MATLAB code.
zeta=0.2
wn=2
transferFunction= tf([wn^2],[1 2*zeta*wn wn^2])
[y,time1]=step(transferFunction);
% create the envelopes
upperEnvelope=1+exp(-zeta*wn*time1)/(sqrt(1-zeta^2));
lowerEnvelope=1-exp(-zeta*wn*time1)/(sqrt(1-zeta^2));
figure(1)
hold on
plot(time1,y,'k')
plot(time1,upperEnvelope,'r')
plot(time1,lowerEnvelope,'m')
The settling time is defined in our previous post which can be found here. Formally speaking, the settling time is defined as follows.
Definition of ![]() settling time: The settling time
settling time: The settling time ![]() is defined as the time required for the transient response to enter and stay within
is defined as the time required for the transient response to enter and stay within ![]() of the steady-state or final value.
of the steady-state or final value.
We can approximately determine the settling time by solving the following equation that is based on the envelope function of the transient response:
(6) ![]()
This approximation is illustrated in the figure below.
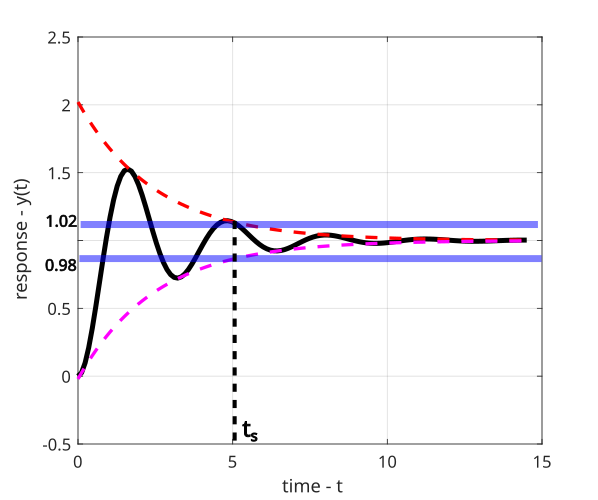
From (6), we obtain
(7) 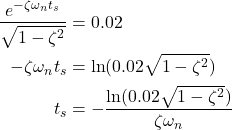
That is, we obtained the following approximation
(8) ![]()
This equation is quite complex, and let us try to simplify this equation. Figure below shows the term ![]() with respect to the parameter
with respect to the parameter ![]() . As the parameter
. As the parameter ![]() is varied from
is varied from ![]() to
to ![]() , the term
, the term ![]() varies from
varies from ![]() to
to ![]() . This variation is illustrated in the figure below.
. This variation is illustrated in the figure below.
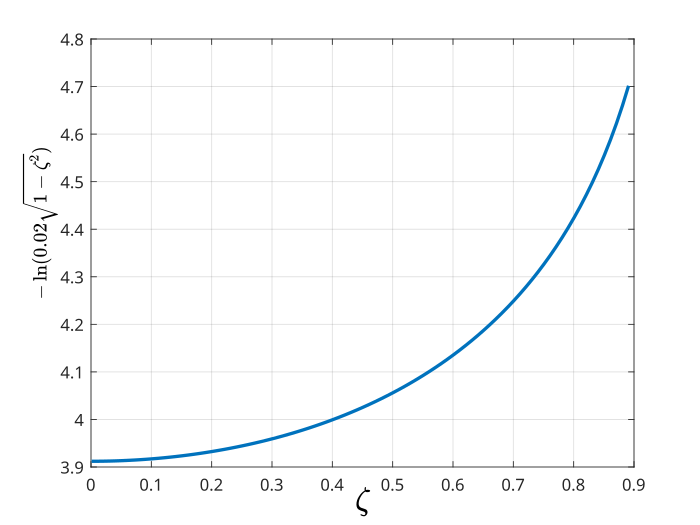
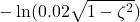 with respect to the parameter
with respect to the parameter  .
.This graph is generated by using the following MATLAB code
zeta=0.001:0.01:0.9
y=-log(0.02*sqrt(1-zeta.^2))
plot(zeta,y)
From this graph, we can observe that we can approximate the term ![]() as follows
as follows
(9) ![]()
By substituting this approximation in (8), we can obtain our final expression for the approximation of the settling time:
(10) ![]()