In this aerospace and robotics tutorial, we explain a very important concept for understanding the kinematics and dynamics of rigid bodies. Namely, we explain the concept of rotation matrices. In this tutorial, we derive the expression for the X-axis rotation matrix and provide a graphical interpretation. The YouTube tutorial accompanying this tutorial is given below.
Let us consider the rotation of one coordinate system with respect to another one which is shown in the figure below.
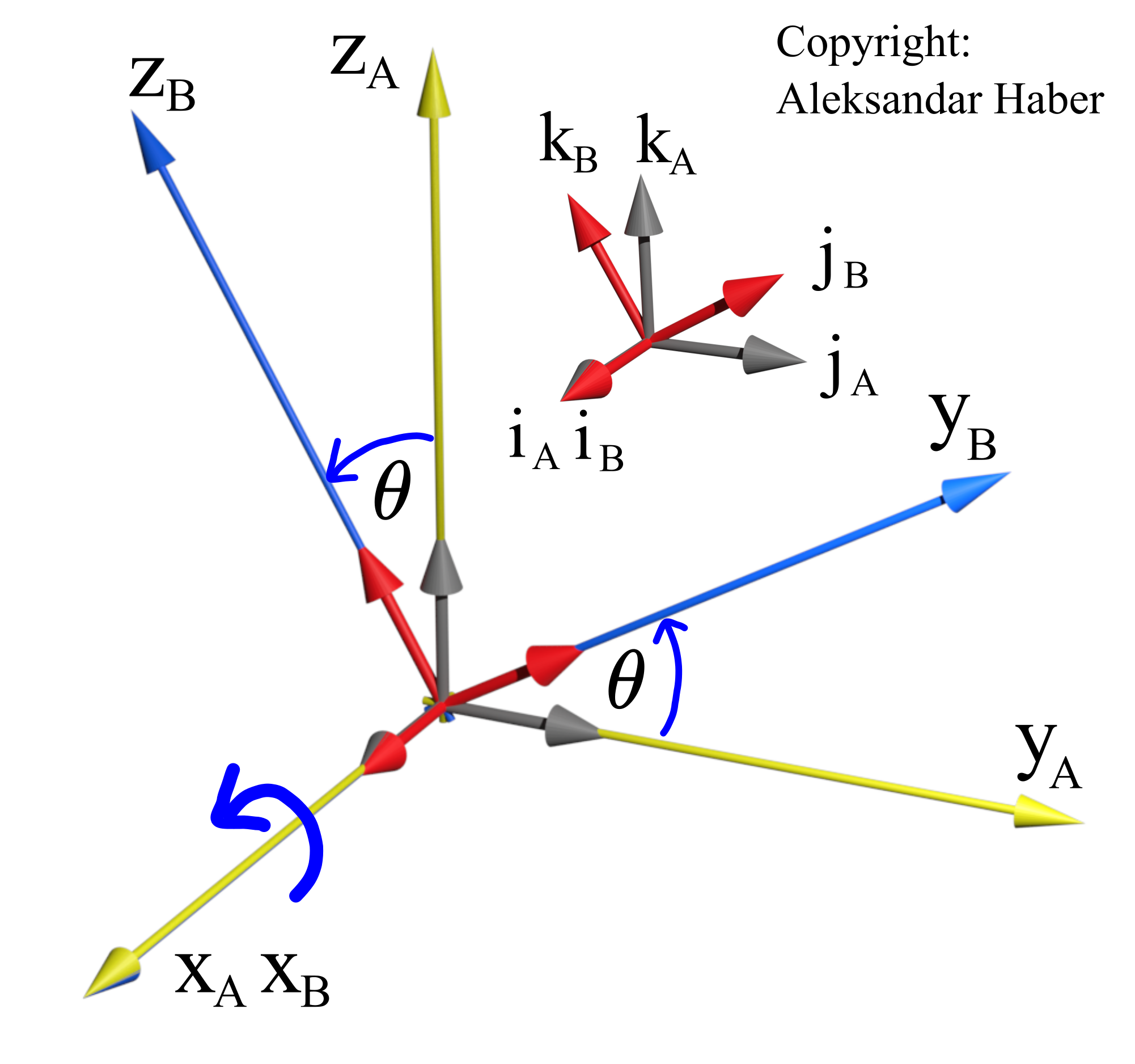
There are two coordinate systems A and B, with the coordinates ![]() and
and ![]() . The coordinate system
. The coordinate system ![]() is rotated with respect to the coordinate system
is rotated with respect to the coordinate system ![]() around the axis
around the axis ![]() for the angle
for the angle ![]() . The unit vectors of the coordinate system
. The unit vectors of the coordinate system ![]() are
are ![]() and
and ![]() . The unit vectors of the coordinate system
. The unit vectors of the coordinate system ![]() are
are ![]() and
and ![]() . We denote vectors by using bold letters.
. We denote vectors by using bold letters.
Next, we introduce the vector ![]() shown in the figure below.
shown in the figure below.
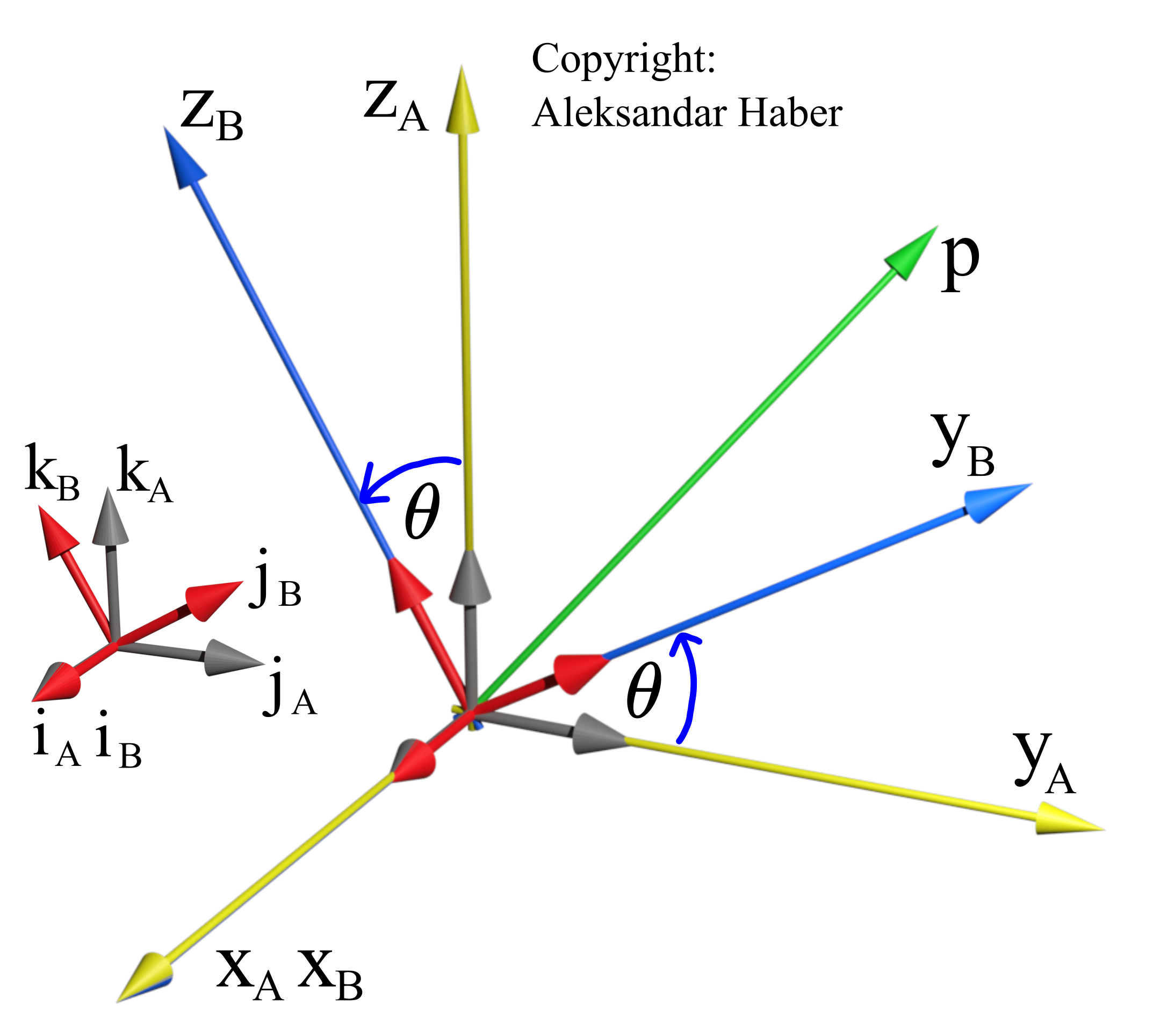
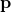 .
.Problem: Knowing the coordinates of the vector ![]() in the coordinate system
in the coordinate system ![]() , and the angle of rotation
, and the angle of rotation ![]() around the axis
around the axis ![]() , find the coordinates of the vector
, find the coordinates of the vector ![]() in the coordinate system
in the coordinate system ![]() .
.
To address this problem, we introduce the following notation:
(1) 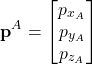
denotes the vector ![]() expressed in the coordinate system
expressed in the coordinate system ![]() . Similarly, the notation
. Similarly, the notation
(2) 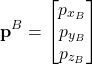
denotes the vector ![]() expressed in the coordinate system
expressed in the coordinate system ![]() .
.
It should be kept in mind that the vectors ![]() and
and ![]() are actually denoting the same vector
are actually denoting the same vector ![]() only expressed in different coordinate systems. The vector
only expressed in different coordinate systems. The vector ![]() expressed in the coordinate system
expressed in the coordinate system ![]() is
is
(3) ![]()
The vector ![]() expressed in the coordinate system
expressed in the coordinate system ![]() is
is
(4) ![]()
Here one thing should always be kept in mind. The unit vectors of both coordinate systems ![]() and
and ![]() are actually expressed in the same basis. That is, they are expressed by using coordinates of some other coordinate system. That is why we can mathematically write:
are actually expressed in the same basis. That is, they are expressed by using coordinates of some other coordinate system. That is why we can mathematically write:
(5) ![]()
That is, we have
(6) ![]()
By substituting (3) and (4) in (6), we have
(7) ![]()
By scalarly multiplying the equation (7) with ![]() , we obtain
, we obtain
(8) ![]()
By scalarly multiplying the equation (7) with ![]() , we obtain
, we obtain
(9) ![]()
By scalarly multiplying the equation (7) with ![]() , we obtain
, we obtain
(10) ![]()
Let us write the equations (8), (9), and (10) together
(11) 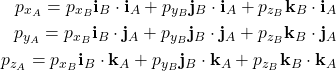
The last three equations can be written in the matrix form as follows
(12) 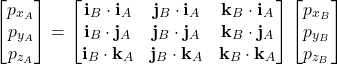
The last equation can be written compactly
(13) ![]()
where
(14) 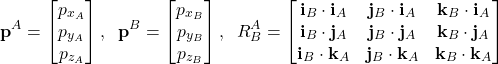
The matrix ![]() is the rotation matrix. The superscript and subscript notations in
is the rotation matrix. The superscript and subscript notations in ![]() mean that the rotation matrix transforms projections of a vector from the coordinate system
mean that the rotation matrix transforms projections of a vector from the coordinate system ![]() into the coordinate system
into the coordinate system ![]() . Let us observe the figure shown below. This figure shows the side view (from the top of the unit vector of the
. Let us observe the figure shown below. This figure shows the side view (from the top of the unit vector of the ![]() axis) of the unit vectors of the coordinate systems
axis) of the unit vectors of the coordinate systems ![]() and
and ![]() .
.
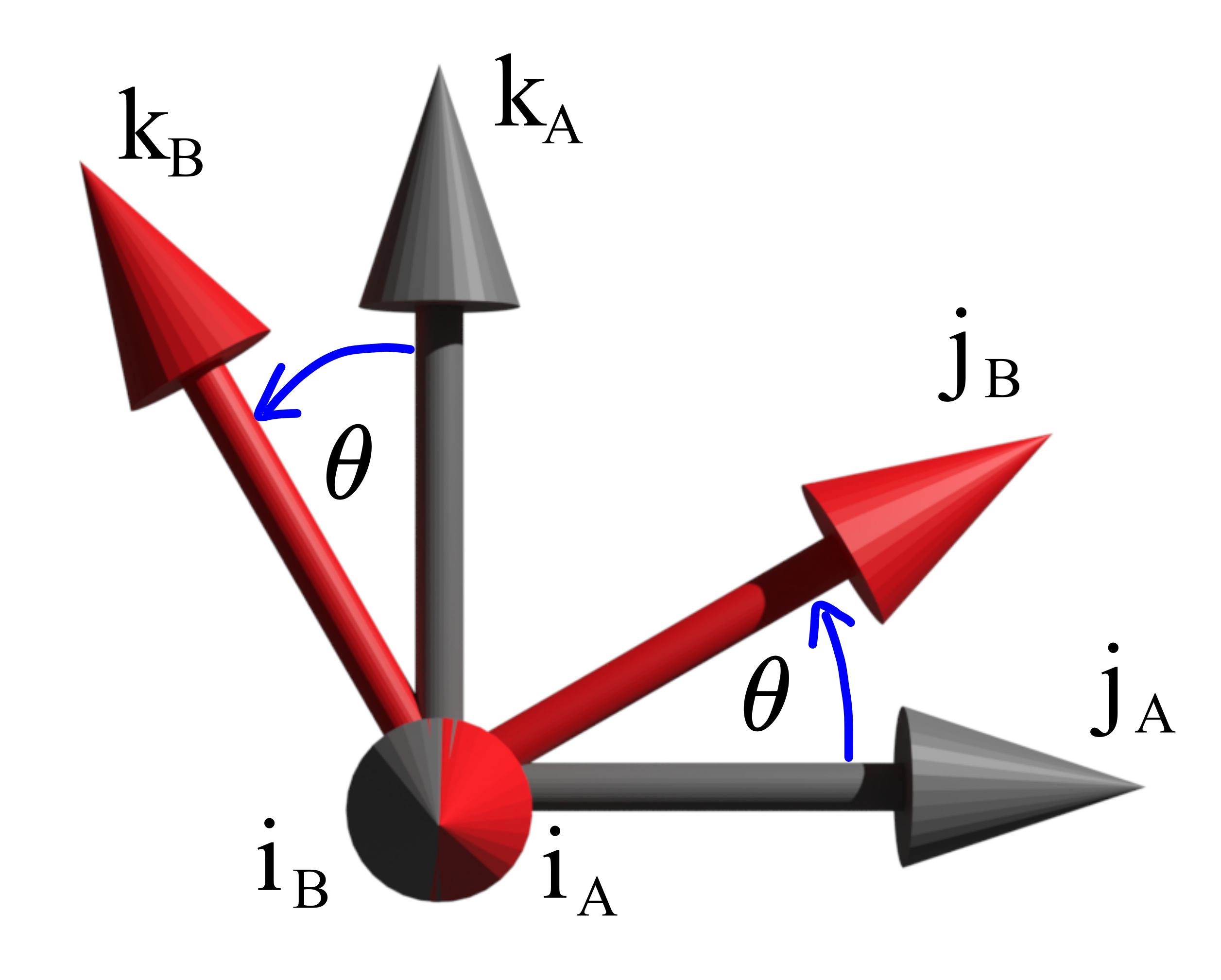
Since the vectors ![]() and
and ![]() are unit vectors, we have
are unit vectors, we have
(15) 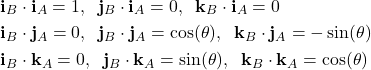
By substituting (15) in (14), we have
(16) 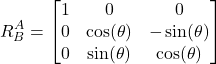
The matrix defined in (16) is the rotation matrix defining the rotation of two coordinate systems around the ![]() axis.
axis.
To summarize, the expression
(17) ![]()
implements a mapping. It transforms the projections of the vector ![]() expressed in the coordinate system
expressed in the coordinate system ![]() , into the projections of the vector
, into the projections of the vector ![]() expressed in the coordinate system
expressed in the coordinate system ![]() .
.
Another important property of the rotation matrices is that they are orthogonal, that is,
(18) ![]()
This is important since from (17), we can write
(19) 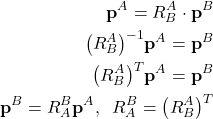
More about the properties of the rotation matrices can be found here.