In this digital signal processing and discrete-time control tutorial, we explain how to calculate the magnitude (amplitude) and phase responses of discrete-time systems and filters. First, we briefly summarize the concept of the frequency response, and then we solve an example. We also explain the concepts of digital frequency, baseband, sampling frequency, and the relation of the digital frequency with the Nyquist frequencies and continuous time angular frequencies. In the second part of this tutorial, given here, we explain how to compute the phase and magnitude response of digital filters in Python.
The YouTube video accompanying this tutorial is given below.
Frequency Response Summary
The basic idea is to start from the transfer function of the discrete-time system that has the following form
(1) ![]()
where ![]() and
and ![]() are real numbers or coefficients of the system (filter), and
are real numbers or coefficients of the system (filter), and ![]() is the complex variable that is associated with the
is the complex variable that is associated with the ![]() -transform. The frequency response is obtained by substituting
-transform. The frequency response is obtained by substituting ![]() with
with
(2) ![]()
where ![]() is the imaginary unit and
is the imaginary unit and ![]() , is often referred to as the digital frequency. Here, it should be noted that
, is often referred to as the digital frequency. Here, it should be noted that ![]() is in the interval
is in the interval ![]() . That is, we only consider this interval when computing the frequency response. The reasons for this will be explained later on in this tutorial. As a result, we obtain the following expression
. That is, we only consider this interval when computing the frequency response. The reasons for this will be explained later on in this tutorial. As a result, we obtain the following expression
(3) 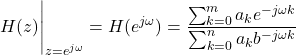
As it will become completely clear after we solve an example, the expression (3) is a complex number or better to say a complex function of ![]() . Consequently, we can represent the complex number (3) in the polar form
. Consequently, we can represent the complex number (3) in the polar form
(4) ![]()
where
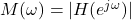 is a function of
is a function of  that is called the magnitude response of the amplitude response of the system.
that is called the magnitude response of the amplitude response of the system.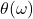 is a function of
is a function of  that is called the phase response of the system.
that is called the phase response of the system.
There are a number of approaches for computing the phase and magnitude responses. We can use the polar form of a complex number to transform expressions in the numerator and denominator of ![]() , and from there we can find the polar form of the complete expression. Another approach for computing the phase and magnitude responses is to represent the complex number
, and from there we can find the polar form of the complete expression. Another approach for computing the phase and magnitude responses is to represent the complex number ![]() in the rectangular form
in the rectangular form
(5) ![]()
where ![]() and
and ![]() are the real and imaginary parts of
are the real and imaginary parts of ![]() . The magnitude response is then
. The magnitude response is then
(6) ![]()
and the phase response is then computed by solving this equation
(7) ![]()
Before we explain how to compute the frequency response it is important to clarify several important things related to the digital frequency ![]() . The digital frequency is defined by
. The digital frequency is defined by
(8) ![]()
where ![]() is the continuous-time (angular or radial) frequency and
is the continuous-time (angular or radial) frequency and ![]() is the sampling period of the discrete-time signal.
is the sampling period of the discrete-time signal.
First of all, the continuous-time sinusoidal signals are quantified by the continuous-time angular frequency ![]() :
:
(9) ![]()
where ![]() is continuous time and
is continuous time and ![]() is equal to
is equal to
(10) ![]()
where ![]() is the period of the continuous-time sinusoidal signal. However, the period of the continuous time signal
is the period of the continuous-time sinusoidal signal. However, the period of the continuous time signal ![]() should not be confused with the sampling period
should not be confused with the sampling period ![]() . If the signal is sampled with the sampling period of
. If the signal is sampled with the sampling period of ![]() , then the time is
, then the time is ![]() , where
, where ![]() is an integer denoting a discrete-time instant. In that case, the continuous-time signal (9) is represented by
is an integer denoting a discrete-time instant. In that case, the continuous-time signal (9) is represented by
(11) ![]()
where ![]() is the digital frequency that we introduced previously. When analyzing the frequency response of discrete-time systems or the spectrum of discrete-time signals, the digital frequency is in the following range
is the digital frequency that we introduced previously. When analyzing the frequency response of discrete-time systems or the spectrum of discrete-time signals, the digital frequency is in the following range
(12) ![]()
This is due to several important reasons. First of all, when analyzing discrete-time signals, we only take into account their continuous-time pairs that are in the frequency range from zero to the continuous-time frequency ![]() , where
, where
(13) ![]()
is the angular sampling frequency and ![]() is the sampling frequency. The frequency
is the sampling frequency. The frequency ![]() or equivalently
or equivalently ![]() are called Nyquist frequencies. If we substitute
are called Nyquist frequencies. If we substitute ![]() for
for ![]() in (8), we obtain
in (8), we obtain
(14) ![]()
That is, the maximal digital frequency that we can take into account is ![]() . On the other hand, for systems that have a real-valued impulse response, the magnitude (amplitude) response is an even function of the digital frequency, and the phase response is an odd function of the digital frequency. This means that for such systems, we can only consider the digital frequency in the range
. On the other hand, for systems that have a real-valued impulse response, the magnitude (amplitude) response is an even function of the digital frequency, and the phase response is an odd function of the digital frequency. This means that for such systems, we can only consider the digital frequency in the range ![]() when computing the frequency response. However, it is a standard practice to consider the full frequency range:
when computing the frequency response. However, it is a standard practice to consider the full frequency range:
(15) ![]()
The interval (15) is often referred to as the digital baseband or simply as baseband.
Another important thing to keep in mind is that due to sampling, the frequency response of the system is periodic with the period of ![]() in the digital frequency domain, or with the equivalent period of
in the digital frequency domain, or with the equivalent period of ![]() in the continuous frequency domain. That is, the magnitude and phase responses in the baseband, repeat themselves with the period of
in the continuous frequency domain. That is, the magnitude and phase responses in the baseband, repeat themselves with the period of ![]() . Due to all these reasons, we only compute the frequency response for the frequencies in the baseband (15).
. Due to all these reasons, we only compute the frequency response for the frequencies in the baseband (15).
Also, the discrete-time transfer function ![]() is the Z-transform of the impulse response of the discrete-time system. Consequently, the function
is the Z-transform of the impulse response of the discrete-time system. Consequently, the function ![]() is the frequency spectrum of the impulse response sequence of the system.
is the frequency spectrum of the impulse response sequence of the system.
Example of Computing Phase and Frequency Response of Discrete-time (Digital) System (Filter)
Let us consider the following discrete-time system
(16) ![]()
where ![]() is the input sequence and
is the input sequence and ![]() is the output sequence. The first step is to derive the transfer function. To do that we apply the Z-transform to (16)
is the output sequence. The first step is to derive the transfer function. To do that we apply the Z-transform to (16)
(17) ![]()
using the following notation
(18) ![]()
, and the fact that ![]() , from (17), we have
, from (17), we have
(19) ![]()
or
(20) ![]()
From the last equation, we have
(21) ![]()
This is the transfer function of the system. Let us compute the frequency response
(22) ![]()
From the last equation, we have
(23) ![]()
The idea for this transformation is to use this formula
(24) ![]()
to eliminate the difference between the complex exponentials and to compute the magnitude response.
From (23), we have
(25) 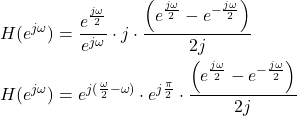
By using (24), from (25) we obtain
(26) ![]()
From this equation, we can conclude that the magnitude response is
(27) ![]()
At first sight, from (26) it looks like the phase response is ![]() . However, this is not a correct conclusion! This is mainly because the sign of the term
. However, this is not a correct conclusion! This is mainly because the sign of the term ![]() changes when
changes when ![]() is varied from
is varied from ![]() to
to ![]() . This means that when
. This means that when ![]()
(28) ![]()
on the other hand, when ![]()
(29) ![]()
This means that the correct phase is given by
(30) 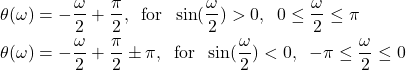
or
(31) 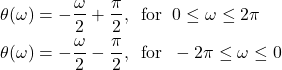
or finally
(32) 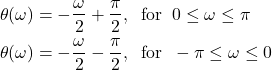
The phase and magnitude responses are shown in the figure below.
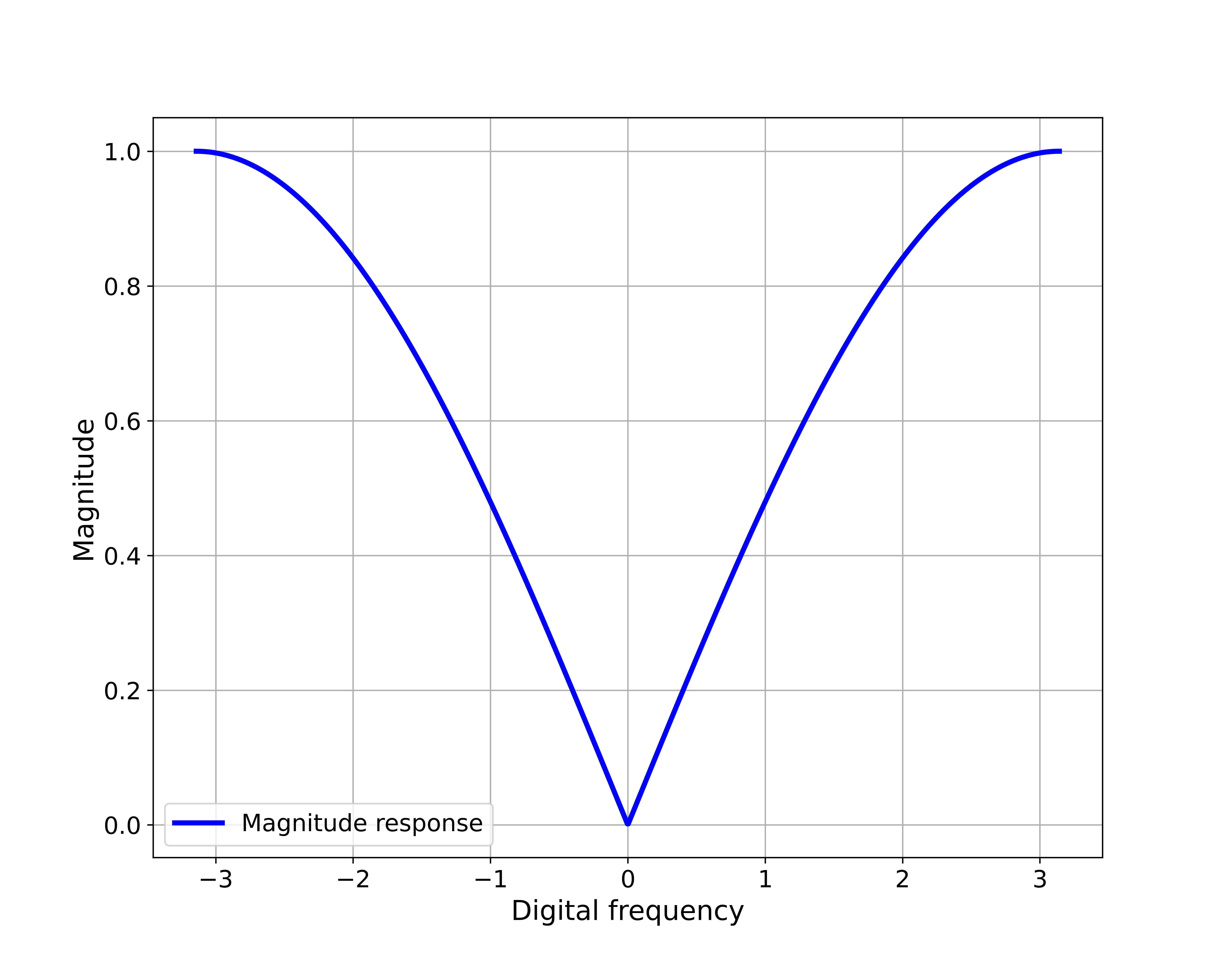
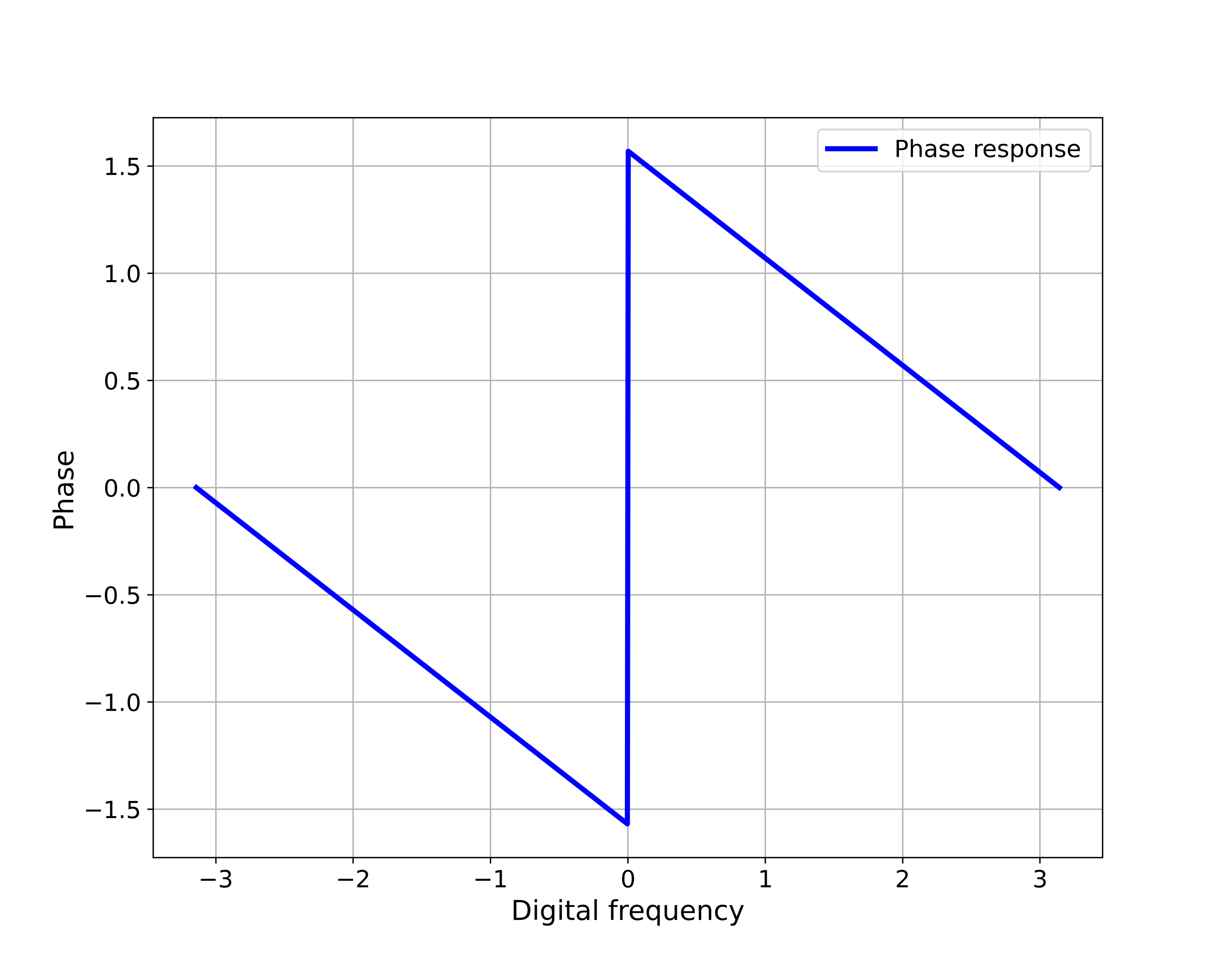
From the magnitude response, we can see that this system attenuates the low frequencies and the high frequencies are not attenuated. That is, this filter acts as a high-pass filter. These two graphs are generated by using the Python code that is explained in the tutorial given here.