In this tutorial, we provide a clear and correct explanation of the linearization of dynamical systems. The motivation for creating this tutorial comes from the fact that online we can find a number of tutorials that do not correctly or clearly explain the linearization process of dynamical systems. Consequently, this tutorial aims to provide a clear, concise, and correct explanation of the linearization process. The YouTube tutorial accompanying this post is given below.
Motivational example
We consider a simple gravity pendulum shown in the figure below.
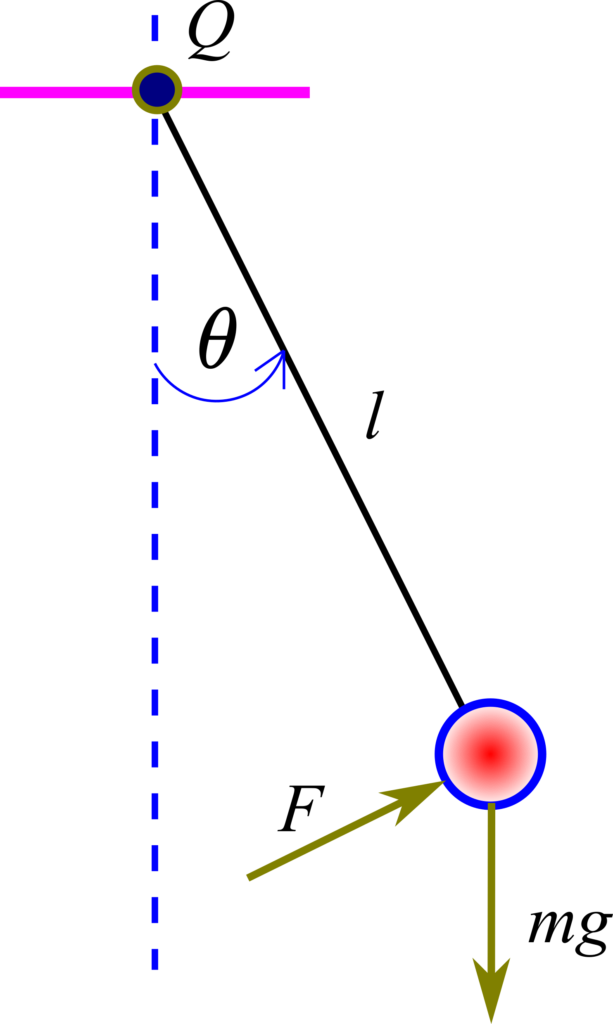
A ball (red color in the figure) with a mass of ![]() is attached by using a massless rod to the pivot point
is attached by using a massless rod to the pivot point ![]() . We assume that the force
. We assume that the force ![]() is acting at the ball. The length of the rod is
is acting at the ball. The length of the rod is ![]() . The force is always perpendicular to the rod. In the figure above,
. The force is always perpendicular to the rod. In the figure above, ![]() is the gravitational acceleration constant. We assume that the mass of the rod is significantly smaller than the mass of the ball and consequently, we can neglect it. The free-body diagram is shown in the figure below.
is the gravitational acceleration constant. We assume that the mass of the rod is significantly smaller than the mass of the ball and consequently, we can neglect it. The free-body diagram is shown in the figure below.
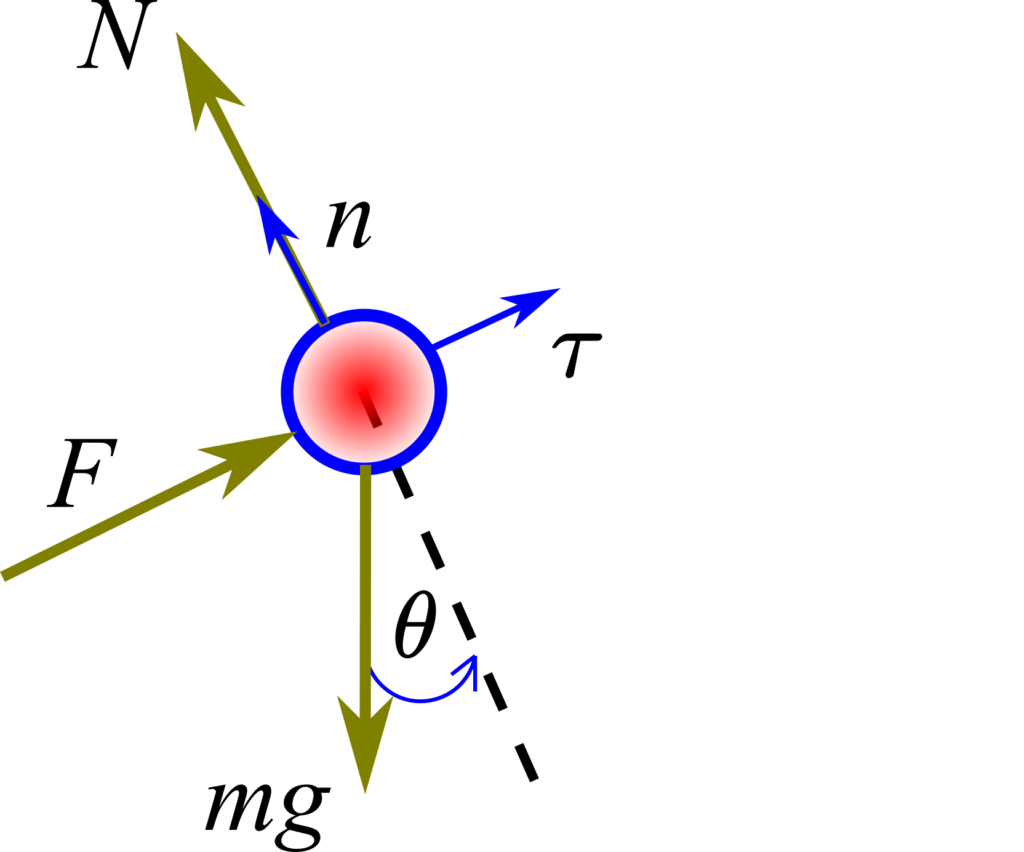
In the figure above, ![]() is the normal reaction force exerted by the rod on the ball,
is the normal reaction force exerted by the rod on the ball, ![]() is the gravitational force,
is the gravitational force, ![]() is the control force,
is the control force, ![]() is the normal unit vector in the direction of the rod, and
is the normal unit vector in the direction of the rod, and ![]() is the tangent unit vector perpendicular to the rod (tangent to the circle describing the trajectory of the ball). Note that
is the tangent unit vector perpendicular to the rod (tangent to the circle describing the trajectory of the ball). Note that ![]() and
and ![]() define two perpendicular axes. From Newton’s law, we obtain
define two perpendicular axes. From Newton’s law, we obtain
(1) ![]()
where ![]() is the acceleration vector. By scalarly multiplying this equation with
is the acceleration vector. By scalarly multiplying this equation with ![]() unit vector, we obtain the projection of this equation onto the
unit vector, we obtain the projection of this equation onto the ![]() axis (tangent axis):
axis (tangent axis):
(2) ![]()
On the other hand, the tangential acceleration is given by
(3) ![]()
where ![]() is the second time derivative of
is the second time derivative of ![]() . The variable
. The variable ![]() is called the angular acceleration. By substituting this expression in the previous equation, we obtain
is called the angular acceleration. By substituting this expression in the previous equation, we obtain
(4) ![]()
From this equation, we obtain
(5) ![]()
For simplicity, we assume that the control force ![]() is equal to
is equal to
(6) ![]()
where ![]() is the control input. Consequently, the final model of the system has the following form
is the control input. Consequently, the final model of the system has the following form
(7) ![]()
Obviously, this system is nonlinear since
- It nonlinearly depends on the dependent variable
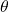 .
. - It nonlinearly depends on the input
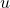 .
.
Let us write the ordinary differential equation (7) in the state-space form. First, we introduce the state-space variables
(8) ![]()
By differentiating the last two equations, we obtain
(9) 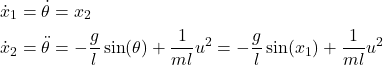
Consequently, the state-space model has the following form
(10) ![]()
Usually, we compactly write this state-space model as follows
(11) ![]()
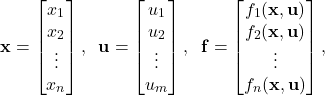
where ![]() is the state vector,
is the state vector, ![]() is the control input vector, and
is the control input vector, and ![]() is a nonlinear vector function of the state vector and input vector. In the general case, these quantities are defined as follows
is a nonlinear vector function of the state vector and input vector. In the general case, these quantities are defined as follows
(12) 
In our case, we have
(13) 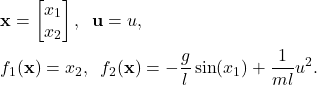
Later in this tutorial, we will get back to our nonlinear model. Next, we explain the linearization process.
Linearization Procedure
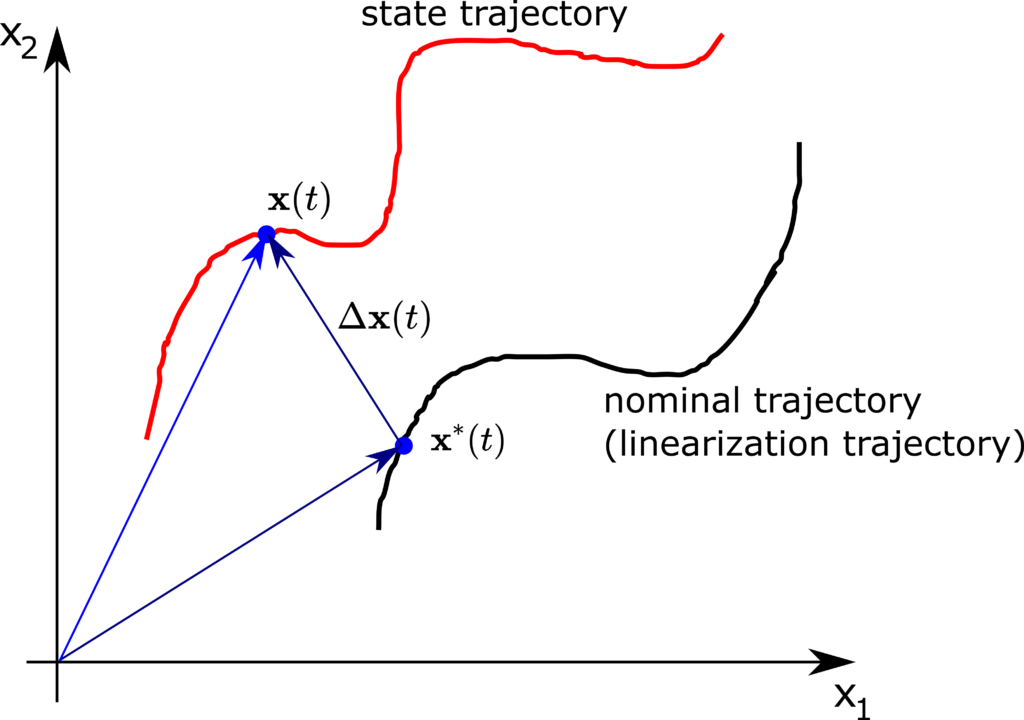
Consider the figure shown below.
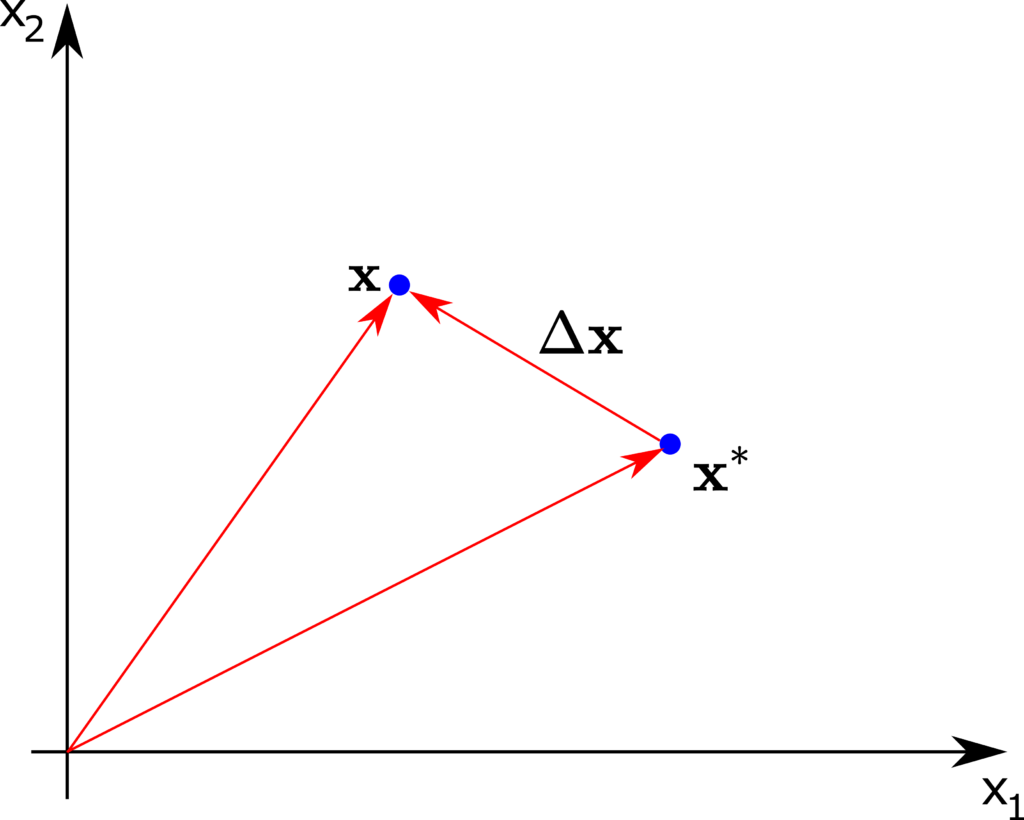
The quantities in this figure are
 is the state vector of the nonlinear system
is the state vector of the nonlinear system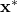 is the state around which we linearize the system
is the state around which we linearize the system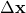 is defined by
is defined by (14)
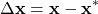
The vector ![]() is the vector of new variables. This vector is the state vector of the linearized system. However, since the input applied to the system can be nonlinear, we need to linearize the system with respect to the input. Consequently, we introduce
is the vector of new variables. This vector is the state vector of the linearized system. However, since the input applied to the system can be nonlinear, we need to linearize the system with respect to the input. Consequently, we introduce
(15) ![]()
Where ![]() is the vector of control inputs around which we linearize the dynamics, and
is the vector of control inputs around which we linearize the dynamics, and ![]() is the control vector in new variables. The vector
is the control vector in new variables. The vector ![]() is the control input vector of the linearized system.
is the control input vector of the linearized system.
When linearizing the dynamics, we have the freedom of choice to choose the vector ![]() . Typical choices are:
. Typical choices are:
- The equilibrium point of the system. That is, the equilibrium point
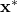 is defined as follows
is defined as follows(16)
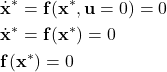
Note here, that the equilibrium points are computed for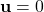 . That is, by assuming that the control input is not affecting the system dynamics.
. That is, by assuming that the control input is not affecting the system dynamics. - The steady state of the system. Let us assume that there is a constant input vector
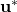 that produces the steady-state
that produces the steady-state 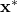 . The vectors
. The vectors 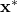 and
and 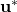 satisfy the following equation
satisfy the following equation (17)
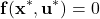
since both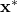 and
and 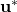 are constants.
are constants. - The nominal trajectory. Instead of selecting the linearization state vector as a steady-state vector or an equilibrium point, the state vector can be selected as a point on a state trajectory. In this case, we have
(18)
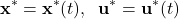
For a known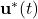 , the state vector
, the state vector 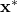 satisfies the following equation
satisfies the following equation(19)
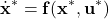
The solution is the nominal state trajectory around which the dynamics is linearized. This type of linearization is shown below.
is the nominal state trajectory around which the dynamics is linearized. This type of linearization is shown below.
Besides these selections, we can also approximate the dynamics around other states and inputs.
The general idea of Linearization
First, let us recall the linearization procedure of nonlinear algebraic functions. Consider the following scalar function ![]() of a scalar argument. This function is illustrated in the figure below.
of a scalar argument. This function is illustrated in the figure below.
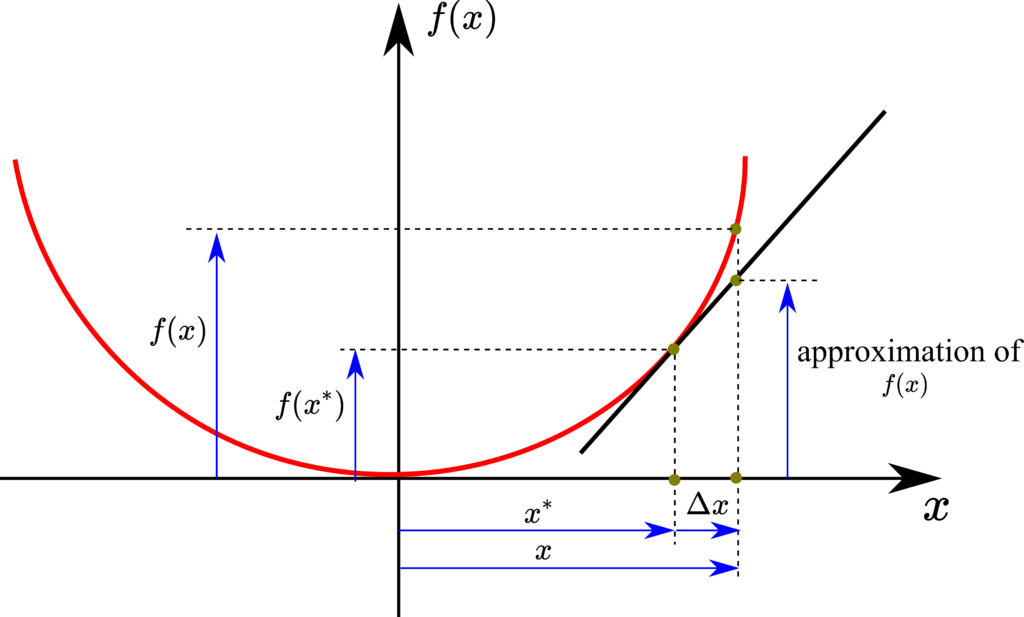
Let us assume that we want to approximate the function ![]() around the point
around the point ![]() . We use the Taylor expansion of the first-order to approximate the function:
. We use the Taylor expansion of the first-order to approximate the function:
(20) 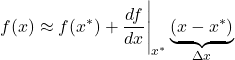
The right-hand side of the last equation is an equation of a tangent line through the point ![]() . This equation has the following mathematical form
. This equation has the following mathematical form
(21) 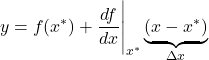
Let us consider the following example
(22) ![]()
Let us approximate this function at the point ![]() . We have
. We have
(23) 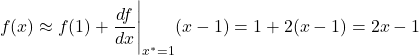
The linearization of nonlinear state-space models is similar in spirit to the linearization of scalar nonlinear functions. In the sequel, we explain the linearization procedure of state-space models.
We approximate the nonlinear function ![]() around the point
around the point ![]() by using the Taylor expansion
by using the Taylor expansion
(24) 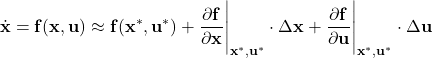
where
(25) ![]()
and where
(26) 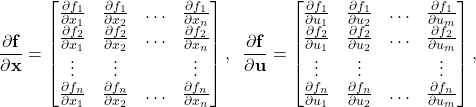
The vertical lines in (24) mean that the matrices are evaluated at the points ![]() and
and ![]() These matrices of partial derivatives with respect to the state and input are called the Jacobian matrices. From (24), we obtain
These matrices of partial derivatives with respect to the state and input are called the Jacobian matrices. From (24), we obtain
(27) 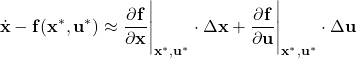
On the other hand, from (25), we obtain
(28) ![]()
Consequently, from (27) and (28), we obtain
(29) 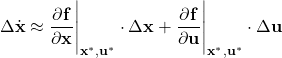
By replacing the approximation with equality, we obtain
(30) 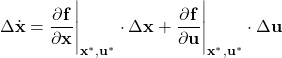
Let us introduce a new notation
(31) 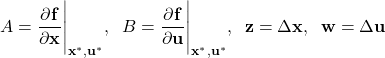
From (30) and (31), we obtain the linearized model
(32) ![]()
where
- The system matrices
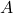 and
and  are defined as follows
are defined as follows
(33) 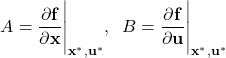
- The linearized state vector and linearized input vector are defined by
(34) ![]()
It should be kept in mind that the linearization produces a reliable approximation of the nonlinear system only for relatively small values of ![]() .
.
Linearization of Nonlinear Pendulum Equations
The nonlinear state-space model is given by the following equation
(35) ![]()
From this equation, we obtain
(36) 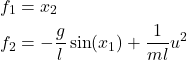
The Jacobian matrix with respect to the state is defined by
(37) 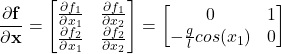
The Jacobian matrix with respect to the control input is defined by
(38) ![]()
We approximate the nonlinear system at the state and input
(39) ![]()
For this selection of the state and input, we obtain
(40) 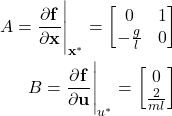
The final linearized model is given by
(41) ![]()