Control Systems Lecture: Laplace Transform – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this post, we introduce an important numerical tool for analyzing and designing control systems. The name of this numerical tool is the Laplace transform. Two YouTube videos accompanying this post are given below.

There are many applications of the Laplace transform in control systems. For example, this transform is used to analyze the stability of control systems. Also, this transform is used to compute the system response to prescribed initial conditions and input signals. Remember that in an ordinary differential equation mathematics course, you have used the Laplace transform to transform linear differential equations into algebraic equations. By manipulating these algebraic equations you were able to solve the original linear differential equations.

So, let us introduce the Laplace transformation. Let $s=\sigma+j \omega$ be a complex variable, where $\sigma$ and $\omega$ are the real and imaginary parts. Let $f(t)$ be a function of time $t$ . Then the Laplace transform of the function $f(t)$ is defined as follows

(1) $\begin{align*}F(s) \triangleq \int_{0^{-}}^{\infty} f(t)e^{-st}dt\end{align*}$

A few comments are in order. The symbol $0^{-}$ means that the integration started at $0-\epsilon$ where epsilon is an infinitesimal quantity. We will often write $0^{-}$ simply as zero. As its name is pointing out, the Laplace transform transforms time-domain function into its complex domain counterpart. The integration is done from $0$ to $\infty$ , and we might ask ourselves, when does this integral exist? We will not go into mathematical details, however, for a large number of functions $f(t)$ , the function $e^{-st}$ prevents the product $f(t) e^{-st}$ from exploding.

Let us now compute Laplace transforms of a few characteristic functions used in control systems.

The Laplace transform of a step function (constant function)

(2) $\begin{align*}& f(t)=c , t\le 0 \notag \\& F(s)=\int_{0}^{\infty} c e^{-st} dt = c \int_{0}^{\infty} e^{-st} dt = \frac{c}{-s} e^{-st} \bigg|^{\infty} _{0}= \frac{c}{-s} \Big(e^{-s\infty} - e^{0} \Big)= \frac{c}{s}\end{align*}$

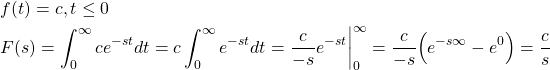
The Laplace transform of a ramp function (constant function)

(3) $\begin{align*}& f(t)=c t , t\le 0 \notag \\& F(s)=\int_{0}^{\infty} c t e^{-st} dt \end{align*}$

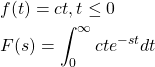
To solve this, we need to use the integration by part rule. There is a simple way to derive the integration by parts rule. Namely, let $u$ and $v$ be two functions, then by differentiating these two functions, we obtain

(4) $\begin{align*}d(u \cdot v)=v \cdot du + u\cdot dv \end{align*}$

From the last equation, we obtain

(5) $\begin{align*}\int v \cdot du = uv - \int u \cdot dv\end{align*}$

So let us apply now the integration by parts to equation (3). By performing the following substitutions

(6) $\begin{align*}v=ct \;\; => dv=c \cdot dt \notag \\du=e^{-st}\;\; => u=\frac{1}{-s} e^{-st}\end{align*}$

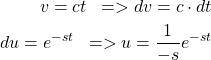
we obtain

(7) $\begin{align*} \int_{0}^{\infty} c t e^{-st} dt = \frac{ct}{-s}e^{-ts}\bigg|^{\infty}_{0}-\int_{0}^{\infty} \frac{c}{-s}e^{-ts} dt\end{align*}$

Let us evaluate the first term

(8) $\begin{align*} \frac{ct}{-s}e^{-ts}\bigg|^{\infty}_{0} = -\frac{ct}{se^{ts}} \bigg|_{t=\infty}-( -\frac{ct}{se^{ts}} ) \bigg|_{t=0} \end{align*}$

The first term is equal to zero since the function $e^{ts}$ grows faster than the function $t$ . Alternatively, you can obtain this result by using the L’Hôpital’s rule. The second term is equal to zero.
By computing the second term in the equation (7), we obtain

(9) $\begin{align*}F(s)=\frac{c}{s^{2}}\end{align*}$

The Laplace Transform of an Exponential function

(10) $\begin{align*}& f(t)=e^{t} , t\le 0 \notag \\& F(s)=\int_{0}^{\infty} e^{t} e^{-st} dt \end{align*}$

We have:

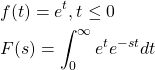
(11) $\begin{align*}F(s)=\int_{0}^{\infty} e^{(1-s)t} dt = \frac{1}{1-s} e^{(1-s)t}\bigg|^{\infty}_{0} \end{align*}$

under the condition that the integral exists (the condition will be explained later). To evaluate the last expression, we need to write the complex variable $s$ as follows $s=\sigma + j\omega$ . Then, we can write

(12) $\begin{align*} e^{(1-s)t}=e^{(1-\sigma)t-j\omega t} = e^{(1-\sigma)t} e^{-j\omega t} \end{align*}$

Next, we need to use the Euler’s formula. This formula has the following form

(13) $\begin{align*}e^{jx}=cos(x)+jsin(x)\end{align*}$

Applying this formula to the equation (12), we obtain

(14) $\begin{align*} e^{(1-s)t} = e^{(1-\sigma)t} \big( cos(\omega t) - j sin(\omega t) \big)\end{align*}$

Under the condition that $1< \sigma$ , the exponent in the last expression is negative. Under this condition, we have

(15) $\begin{align*} e^{(1-s)t} \bigg|^{\infty}_{0} = -1 \end{align*}$

since $e^{(1-\sigma)\infty} =0$ and $e^{(1-\sigma)0} =1$ . Substituting this expression in the equation (11), we obtain

(16) $\begin{align*} F(s) = \frac{1}{s-1}\end{align*}$

The Laplace transform of a Harmonic function (sinusoidal function)

(17) $\begin{align*}& f(t)= sin (wt) , t\le 0 \notag \\& F(s)=\int_{0}^{\infty} sin(wt) e^{-st} dt \end{align*}$

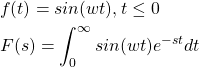
where $w$ is constant. To solve this problem, we need to recall the Euler’s formula. This formula has the following form

(18) $\begin{align*}e^{jx}=cos(x)+jsin(x)\end{align*}$

Using this formula, we can write

(19) $\begin{align*}sin(wt)=\frac{e^{jwt}-e^{-jwt}}{2j}\end{align*}$

By substituting the equation (19) in the equation (17), we obtain

(20) $\begin{align*} F(s) =\int_{0}^{\infty} \frac{e^{(jw-s)t}- e^{-(jw+s)t}}{2j} dt\end{align*}$

The Laplace transform of a step function (constant function)

The Laplace transform of a ramp function (constant function)

The Laplace Transform of an Exponential function

The Laplace transform of a Harmonic function (sinusoidal function)

admin

You might also like

What is Dead Reckoning – Clear Explanation with Python Simulation – Part I

How to Design Parameter of Proportional-Integral Controllers by Using Routh-Hurwitz Stability Test

What is a Characteristic Polynomial of a Matrix?