In this lecture, we explain temperature-induced deformation and stress. The YouTube video accompanying this post is given below.
Consider an object whose 2D projection is shown in Fig. 1.
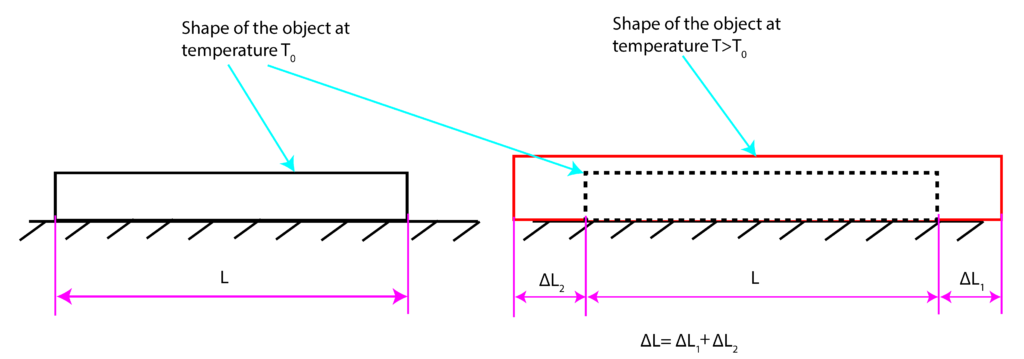
Let us assume that the shape of the object at temperature ![]() is shown in the left part of Fig. 1. Furthermore, let us assume that the temperature of the object is increased to temperature
is shown in the left part of Fig. 1. Furthermore, let us assume that the temperature of the object is increased to temperature ![]() , where
, where ![]() . Obviously, object dimensions will change in the horizontal and vertical directions. For presentation clarity, let us focus on the expansion in the horizontal direction. The left side of the object expands for
. Obviously, object dimensions will change in the horizontal and vertical directions. For presentation clarity, let us focus on the expansion in the horizontal direction. The left side of the object expands for ![]() and the right side expands for
and the right side expands for ![]() . The total deformation is
. The total deformation is
(1) ![]()
Under the assumption that the material properties are homogeneous, we have the following formula that relates total deformation ![]() and temperature change
and temperature change ![]() :
:
(2) ![]()
where ![]() is the coefficient of thermal expansion,
is the coefficient of thermal expansion, ![]() is the initial length in the horizoncal direction, and where
is the initial length in the horizoncal direction, and where
(3) ![]()
The unit for the coefficient of thermal expansion is ![]() (“one over Kelvin”). Every material has a different value of the coefficient of thermal expansion, and typically, this coefficient is in the range of
(“one over Kelvin”). Every material has a different value of the coefficient of thermal expansion, and typically, this coefficient is in the range of ![]()
![]() .
.
If we divide the equation (2) by ![]() , we obtain
, we obtain
(4) ![]()
where ![]() is the thermal strain.
is the thermal strain.
Here it should be emphasized that if the deformation of the object is not constrained, then temperature increase will not in the general case induce internal stresses.
On the other hand, if the deformation is constrained, then, generally speaking, a temperature increase will introduce internal stresses. The following example explains this phenomenon.
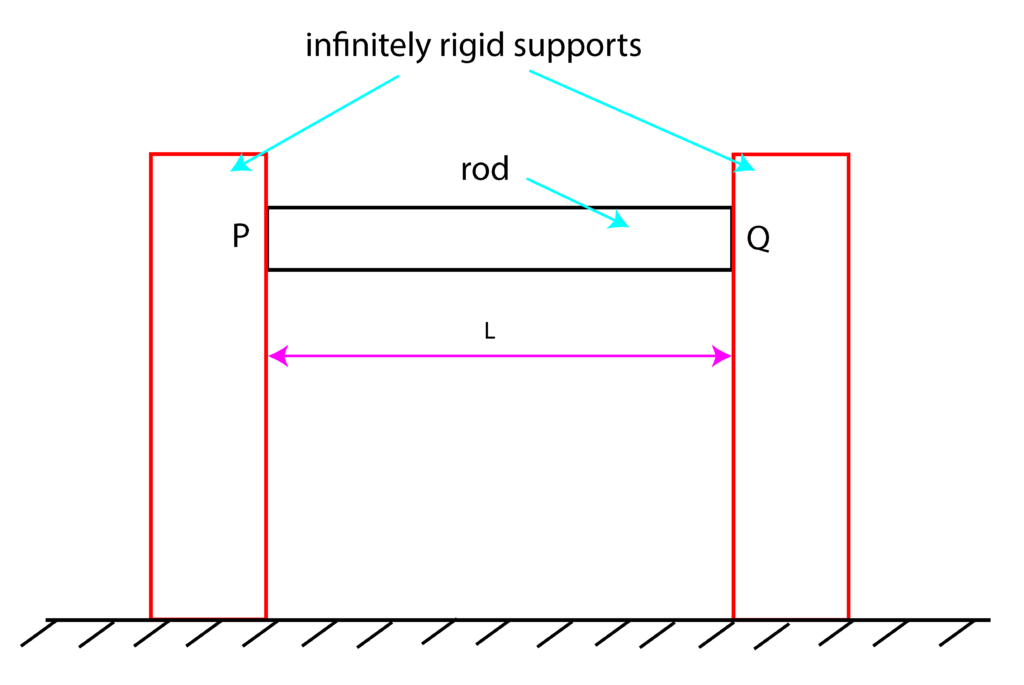
Example: A rod of length ![]() , with the modulus of elasticity of
, with the modulus of elasticity of ![]() , coefficient of thermal expansion
, coefficient of thermal expansion ![]() , and with the cross-section area
, and with the cross-section area ![]() , is supported by two infinitely rigid supports (“infinitely rigid” means that the supports are not deforming when the force is applied to them). Assume that at the temperature
, is supported by two infinitely rigid supports (“infinitely rigid” means that the supports are not deforming when the force is applied to them). Assume that at the temperature ![]() , the reaction forces at the sides
, the reaction forces at the sides ![]() and
and ![]() are approximately equal to zero. Calculate reaction forces and temperature-induced stresses when the temperature is increased to temperature
are approximately equal to zero. Calculate reaction forces and temperature-induced stresses when the temperature is increased to temperature ![]() , where
, where ![]() .
.
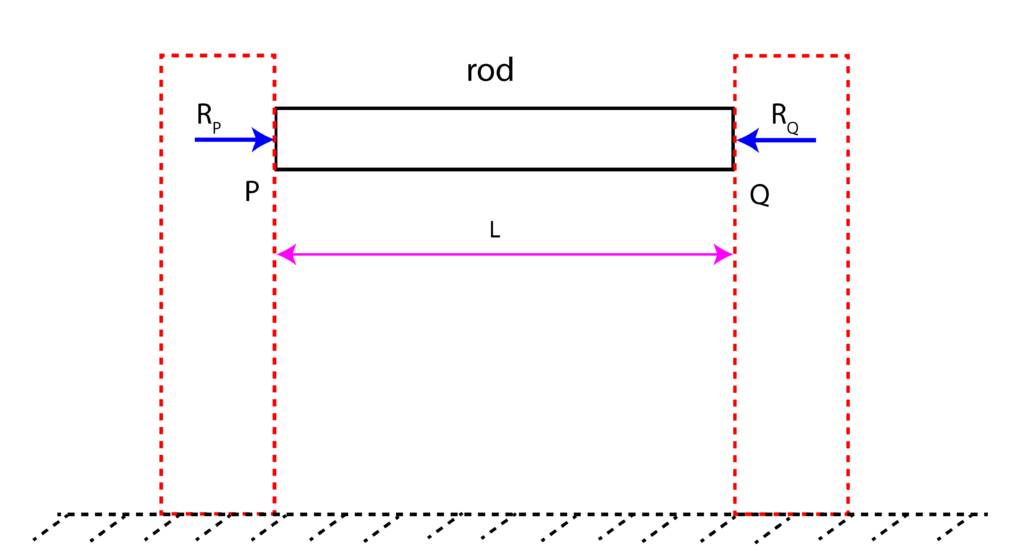
Solution: at the temperature ![]() , we have two reaction forces
, we have two reaction forces ![]() and
and ![]() that are illustrated in Fig. 3 below.
that are illustrated in Fig. 3 below.
 and
and 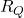 .
.To solve this problem, we apply the superposition principle. Figure 4 below summarizes the superposition principle.
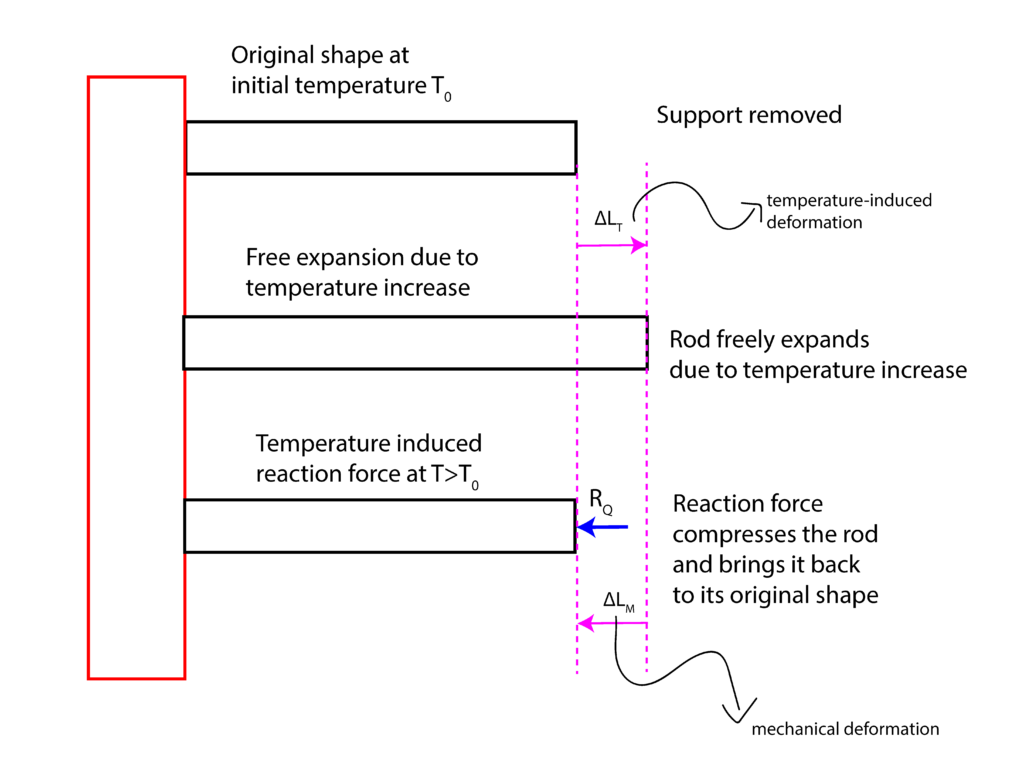
First, in our minds, we can remove the support ![]() . Since the support is removed, the rod will freely expand due to the temperature increase. This deformation is denoted by
. Since the support is removed, the rod will freely expand due to the temperature increase. This deformation is denoted by ![]() , where the subscript “T” stands for “thermal”. Using the formula (2), we have
, where the subscript “T” stands for “thermal”. Using the formula (2), we have
(5) ![]()
Next, we can add reaction force ![]() that will compress the rod and that will bring it back to its original shape. This deformation is equal to
that will compress the rod and that will bring it back to its original shape. This deformation is equal to ![]() , where the subscript “M” stands for “mechanical”. This mechanical deformation can be computed using the classical formula explained in our previous lecture that can be found here. Since
, where the subscript “M” stands for “mechanical”. This mechanical deformation can be computed using the classical formula explained in our previous lecture that can be found here. Since ![]() will induce the compressive internal force (sketch an internal force diagram), we have
will induce the compressive internal force (sketch an internal force diagram), we have
(6) ![]()
where ![]() should be the initial length. Here we have made an approximation that the initial length is approximately equal to
should be the initial length. Here we have made an approximation that the initial length is approximately equal to ![]() . However, in reality, the initial length is
. However, in reality, the initial length is ![]() .
. ![]() is usually very small, and because of that, the approximation is valid. Since absolute values of thermal and mechanical deformation are identical, we have
is usually very small, and because of that, the approximation is valid. Since absolute values of thermal and mechanical deformation are identical, we have
(7) 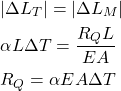
From the static equilibrium condition, we have that ![]() . The thermally induced stress is given by
. The thermally induced stress is given by
(8) ![]()
where the minus sign denotes the fact that the stress is compressive. This solves the problem.