In this tutorial, we will learn how to solve Ordinary Differential Equations (ODEs) in Python by using the odeint() function. The YouTube page accompanying this tutorial is given below.
Test Problem – Pendulum Ordinary Differential Equation
In this tutorial, we consider the following ODE, describing the dynamics of the pendulum system. In our previous post, whose link can be found here, we explained how to derive this equation. The equation takes the following form
(1) ![]()
where ![]() is an angle or rotation measured from the vertical axis and
is an angle or rotation measured from the vertical axis and ![]() and
and ![]() are constants, and the dots above variables denote first or second derivatives with respect to time.
are constants, and the dots above variables denote first or second derivatives with respect to time.
State-space Form of Ordinary Differential Equation
The first step that needs to be performed when solving ODEs is to transform an ODE into a system of first-order differential equations. That is, the first step is to transform the ODE into a state-space form. We introduce state-space variables as follows
(2) ![]()
where ![]() and
and ![]() are new variables called the state-space variables. By using these newly introduced variables, and by using the ODE (1), we can write
are new variables called the state-space variables. By using these newly introduced variables, and by using the ODE (1), we can write
(3) ![]()
The last equation can be written compactly
(4) ![]()
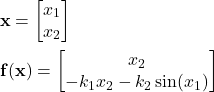
where ![]() is the state vector and
is the state vector and ![]() is a nonlinear vector function defined by
is a nonlinear vector function defined by
(5) 
Solution of the Problem by Using the odeint() Python Function
The first step is to import the necessary libraries
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
First, we import the NumPy library. Then we import the odeint() function from scipy.integrate. The SciPy library provides algorithms for numerical analysis, optimization, and integration of differential equations. Finally, we import the plotting tools.
Next, we need to define a Python function that will represent our ODE. This function is defined by the following code lines
def rightSideODE(x,t,k1,k2):
dxdt=[x[1],-k1*x[1]-k2*np.sin(x[0])]
return dxdt
Basically, the first argument is “x”. It is a row vector representing the state-space variables ![]() and
and ![]() . These are the dependent variables. The second argument is time
. These are the dependent variables. The second argument is time ![]() . This is an independent variable. The last two arguments
. This is an independent variable. The last two arguments ![]() and
and ![]() are the constants defining our ODE. This function should compute and return the right-hand side of the equation (4). That is, the right-hand side of our state-space model. The right hand-side is defined by
are the constants defining our ODE. This function should compute and return the right-hand side of the equation (4). That is, the right-hand side of our state-space model. The right hand-side is defined by
[x[1],-k1*x[1]-k2*np.sin(x[0])]
Once we have defined our ODE, we need to define the initial condition, integration time points, and the constants ![]() and k_{2}. This can be done by using the following code lines:
and k_{2}. This can be done by using the following code lines:
# set the initial conditions
x0=[0,1]
# define the discretization points
timePoints=np.linspace(0,100,300)
#define the constants
k1=0.1
k2=0.5
Finally, we call the odeint() function and plot the results:
solutionOde=odeint(rightSideODE,x0,timePoints, args=(k1,k2))
plt.plot(timePoints, solutionOde[:, 0], 'b', label='x1')
plt.plot(timePoints, solutionOde[:, 1], 'g', label='x2')
plt.legend(loc='best')
plt.xlabel('time')
plt.ylabel('x1(t), x2(t)')
plt.grid()
plt.savefig('simulation.png')
plt.show()
The main part of this code is the function call:
solutionOde=odeint(rightSideODE,x0,timePoints, args=(k1,k2))
The first argument is the name of the function that defines the ODE. In our case, the name of the function is “rightSideODE”. The second argument is the row vector x0 defining the initial conditions. The third argument is the row vector containing time points at which the solution is computed. The final argument contains the constants ![]() and k_{2}. This code produced the following graph.
and k_{2}. This code produced the following graph.
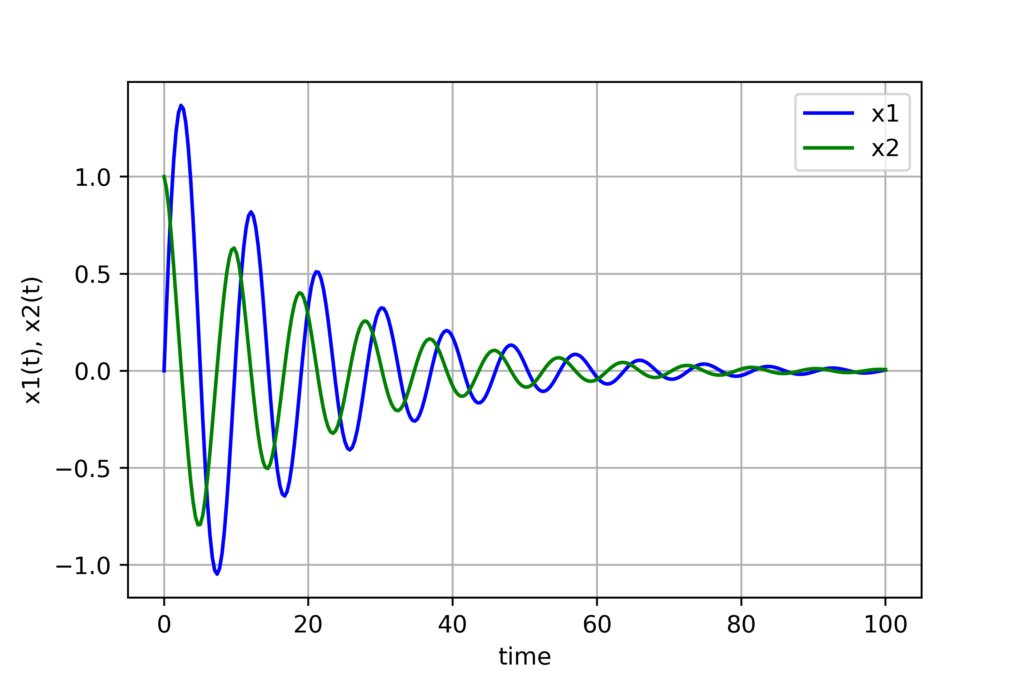
The complete code used in this post is given below.
# -*- coding: utf-8 -*-
"""
Created on Mon Oct 10 18:27:57 2022
@author: aleks
"""
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def rightSideODE(x,t,k1,k2):
dxdt=[x[1],-k1*x[1]-k2*np.sin(x[0])]
return dxdt
# set the initial conditions
x0=[0,1]
# define the discretization points
timePoints=np.linspace(0,100,300)
#define the constants
k1=0.1
k2=0.5
solutionOde=odeint(rightSideODE,x0,timePoints, args=(k1,k2))
plt.plot(timePoints, solutionOde[:, 0], 'b', label='x1')
plt.plot(timePoints, solutionOde[:, 1], 'g', label='x2')
plt.legend(loc='best')
plt.xlabel('time')
plt.ylabel('x1(t), x2(t)')
plt.grid()
plt.savefig('simulation.png')
plt.show()