November 2, 2024
Uncategorized

Routh-Hurwitz Stability Criterion and Test (no special cases)

adminby admin

The main idea of the Routh-Hurwitz stability test is to determine if a system is asymptotically stable without explicitly finding the roots of the characteristic polynomial. This criterion originated before the digital computer age. However, it is still very useful since it can give us a range of control parameters that will guarantee system stability. The YouTube video accompanying this post is given here:

Let the characteristic polynomial of the system whose stability we want to investigate be given by the following equation

(1)   \begin{align*}w(s)=s^6+a_{1}s^{5}+a_{2}s^{4}+a_{3}s^{3}+a_{4}s^{2}+a_{5}s^{2}+a_{6}\end{align*}

Here for presentation clarity, we assumed a system whose model order is equal to n=6. However, everything explained in this post can be generalized to systems with arbitrary state order.

Necessary conditions for stability are that all coefficients of the characteristic polynomial (1) have the same sign and that none of the coefficients vanishes. However, these are NOT sufficient conditions. The Routh-Hurwitz stability criterion gives us the necessary and sufficient conditions. To apply this criterion, we need to construct the Routh-Hurwitz table. This table is constructed as follows:

1a_{2}a_{4}a_{6}
a_{1}a_{3}a_{5}0
a_{31}=\frac{a_{1}a_{2}-a_{3}}{a_{1}}a_{32}=\frac{a_{1}a_{4}-a_{5}}{a_{1}}a_{33}=\frac{a_{1}a_{6}}{a_{1}}0
a_{41}=\frac{a_{31}a_{3}-a_{32}a_{1}}{a_{31}}a_{42}=\frac{a_{31}a_{5}-a_{33}a_{1}}{a_{31}}00
a_{51}=\frac{a_{41}a_{32}-a_{31}a_{42}}{a_{41}}a_{52}=\frac{a_{41}a_{33}}{a_{41}}00
a_{61}=\frac{a_{51}a_{42}-a_{52}a_{41}}{a_{51}}000
a_{71}=\frac{a_{61}a_{52}}{a_{61}}000
Routh-Hurwitz table for testing the stability of the system.

Here is an explanation of how this table is constructed. The first row is constructed by filling even characteristic polynomial coefficient starting from the coefficient a_{0} that is equal to 1. The second row is constructed by filling odd coefficients starting from a_{1}. Then, the third row is constructed as follows:

(2)   \begin{align*}a_{31}&=-\frac{\text{det}\begin{bmatrix} 1 & a_{2} \\ a_{1} & a_{3} \end{bmatrix}}{a_{1}}= -\frac{a_{3}-a_{1}a_{2}}{a_{1}}=\frac{a_{1}a_{2}-a_{3}}{a_{1}} \\a_{32}& =-\frac{\text{det}\begin{bmatrix} 1 & a_{4} \\ a_{1} & a_{5} \end{bmatrix}}{a_{1}} = -\frac{a_{5}-a_{4}a_{1}}{a_{1}}=\frac{a_{4}a_{1}-a_{5}}{a_{1}} \\a_{33}& = -\frac{\text{det}\begin{bmatrix} 1 & a_{6} \\ a_{1} & 0 \end{bmatrix}}{a_{1}}=-\frac{-a_{6}a_{1}}{a_{1}}=\frac{a_{6}a_{1}}{a_{1}} \end{align*}

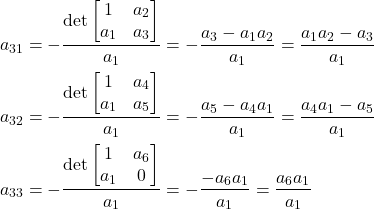
The fourth row is constructed in a similar manner

(3)   \begin{align*} a_{41}&=-\frac{\text{det}\begin{bmatrix}a_{1} & a_{3} \\ a_{31} & a_{32} \end{bmatrix}}{a_{31}}= -\frac{a_{1}a_{32}-a_{3}a_{31}}{a_{31}}=\frac{a_{3}a_{31}-a_{1}a_{32}}{a_{31}} \\a_{42}& =-\frac{\text{det}\begin{bmatrix} a_{1} & a_{5} \\ a_{31} & a_{33} \end{bmatrix}}{a_{31}} = -\frac{a_{1}a_{33}-a_{5}a_{31}}{a_{31}}=\frac{a_{5}a_{31}-a_{1}a_{33}}{a_{31}} \end{align*}

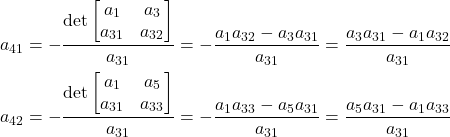
By using this principle, we can construct all other entries in the table.

The Routh-Hurwitz stability test investigates the sign of the entries of the first column of the table.

The roots of the characteristic polynomial are all in the left half of the s-plane if all the entries of the first column of the Ruth-Hurwitz table have the same sign. Moreover, the number of sign changes of the entries of the first column is equal to the number of poles (roots of the characteristic polynomial) that are in the right half of the s plane.

In this post, we do not cover special cases of the Ruth-Hurwitz test. Special cases occur when the first entry in any of the rows is zero or when all entries in a row are zero. These special cases will be covered in our future posts.

In the sequel, we present several examples in order to illustrate the Routh-Hurwitz criterion.

Example 1: Investigate the stability of a system whose characteristic polynomial is

(4)   \begin{align*}w(s)= s^{3}-4s^{2}+s+6\end{align*}

Solution: We can immediately see that the coefficients of this polynomial do not have the same sign. Consequently, this system is not stable. In this case, the Ruth-Hurwitz test can reveal how many roots of the characteristic polynomial are in the right half of the s plane. Let us construct the test table.

11
-46
a_{31}=-\frac{6-(-4)}{-4}=\frac{10}{4}=\frac{5}{2}0
a_{41}=-\frac{-6\frac{5}{2}}{\frac{5}{2}}=60
Routh-Hurwitz table for testing the stability of the system.

By inspecting the first column, we can observe two sign changes. From 1 to -4, and from -4 to \frac{5}{2}. Consequently, the characteristic polynomial has two roots in the right half of the complex plane. In fact, we can factorize the characteristic polynomial as follows:

(5)   \begin{align*}w(s)=(s-2)(s-3)(s+1)=0\end{align*}

And the poles are s=2, s=3, and s=-1. This completes the example.

Example 2: Investigate the stability of a system whose characteristic polynomial is

(6)   \begin{align*}w(s)= s^{6}+4s^{5}+3s^{4}+2s^{3}+s^{2}+4s+4\end{align*}

Solution: We can immediately observe that all the coefficients have the same sign and there are no zero coefficients. We proceed with the construction of the table. The table is given below.

1314
4240
\frac{12-2}{4}=\frac{5}{2}\frac{4-4}{4}=0\frac{16}{4}=40
\frac{2\frac{5}{2}}{\frac{5}{2}}=2\frac{\frac{5}{2}4-16}{\frac{5}{2}}=-\frac{12}{5}00
\frac{-(\frac{5}{2})(-\frac{12}{5})}{2}=3\frac{2\cdot 4}{2}=400
\frac{3(-\frac{12}{5})-8}{3}=-\frac{76}{15}000
\frac{-\frac{76}{15}\cdot 4}{-\frac{76}{15}}=4000
Routh-Hurwitz table for testing the stability of the system.

Since the coefficients do not have the same sign, we conclude that the system has poles in the right half of the s plane. Consequently, the system is not stable.

admin

View all posts by admin →

You might also like

Some questions for the midterm exam

Basics of Unit Conversion

Fanuc Robot Tutorial 1: Starting the Robot, Clearing Faults, and Jogging Modes (Joint and World)