In this lecture, we explain Poisson’s ratio.
Consider the situation shown in Fig. 1 below.
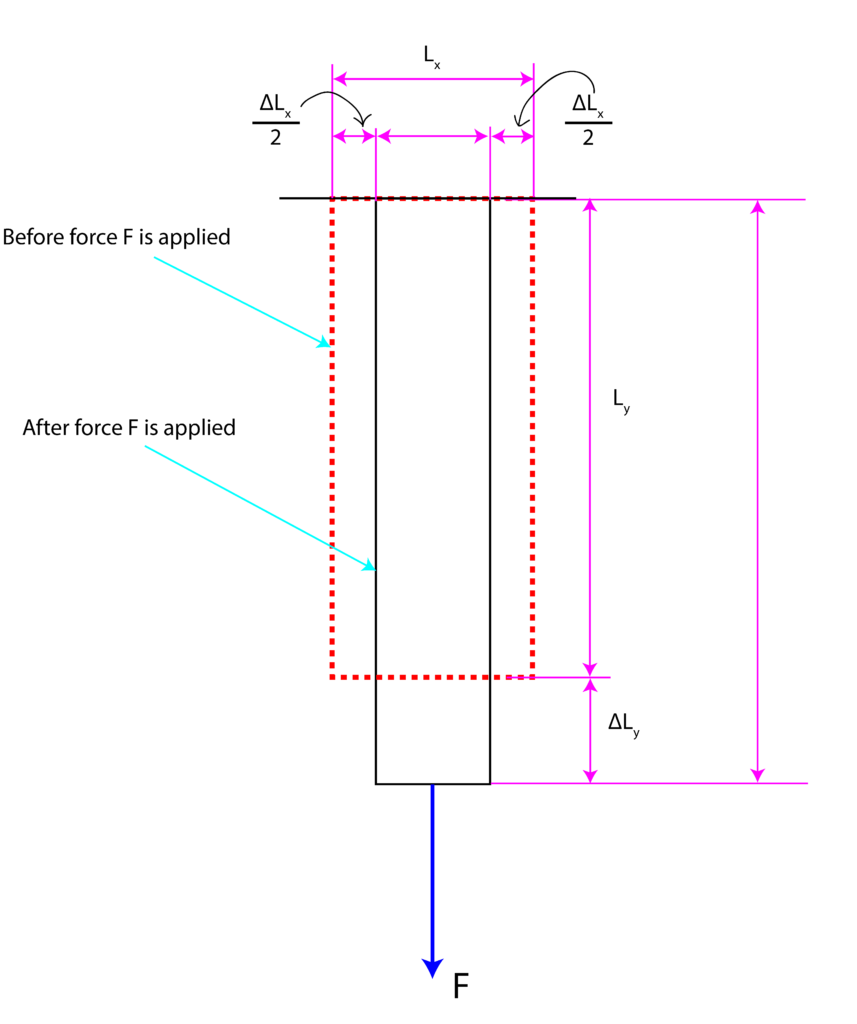
Force ![]() is applied in the
is applied in the ![]() direction. We assume that the produces stress is in the elastic range. That is, the stress is smaller than the elastic limit. Naturally, the element will expand in the
direction. We assume that the produces stress is in the elastic range. That is, the stress is smaller than the elastic limit. Naturally, the element will expand in the ![]() direction. For most of the materials used in engineering practice, this elongation in the
direction. For most of the materials used in engineering practice, this elongation in the ![]() direction will produce deformation in the
direction will produce deformation in the ![]() direction. Also, in the majority of deformation cases, expansion in one direction will produce contraction in the
direction. Also, in the majority of deformation cases, expansion in one direction will produce contraction in the ![]() -direction (direction perpendicular to the action of the force). The initial shape of the element is denoted by the red dashed line. The final deformation after the action of force
-direction (direction perpendicular to the action of the force). The initial shape of the element is denoted by the red dashed line. The final deformation after the action of force ![]() is denoted by the black solid line. The strain in the
is denoted by the black solid line. The strain in the ![]() direction is defined by
direction is defined by
(1) ![]()
where ![]() is the deformation in the
is the deformation in the ![]() direction, defined by
direction, defined by
(2) ![]()
where ![]() and
and ![]() are the final and initial deformations in the
are the final and initial deformations in the ![]() direction. On the other hand, the strain in the
direction. On the other hand, the strain in the ![]() direction is defined by
direction is defined by
(3) ![]()
where ![]() is the deformation in the
is the deformation in the ![]() direction, defined by
direction, defined by
(4) ![]()
where ![]() and
and ![]() are the final and initial deformations in the
are the final and initial deformations in the ![]() direction. Here it should be emphasized that
direction. Here it should be emphasized that ![]() has a negative sign since it is assumed that
has a negative sign since it is assumed that ![]() .
.
Poisson’s ratio is defined by
(5) ![]()
The minus sign comes from the fact that ![]() is negative and we have to add a minus sign in order to make Poisson’s ratio
is negative and we have to add a minus sign in order to make Poisson’s ratio ![]() positive.
positive.
For most of the materials used in the practice Poisson’s ratio is in the range of 0 to 0.5. For most of the solids, Poisson’s ratio is in the range of 0.2 to 0.3. For example, Aluminum alloys have Poisson’s ratio in the range of 0.32 to 0.35. Steel alloys have Poisson’s ratio in the range of 0.28 to 0.31.
A nice summary of Poisson’s ratio with values for typical materials used in practice is given here.