Model Predictive Control (MPC) Tutorial 1: Unconstrained Formulation, Derivation, and Implementation in Python from Scratch

In this control engineering, control theory, and machine learning, we present a Model Predictive Control (MPC) tutorial. First, we explain how to formulate the problem and how to solve it. Finally, we explain how to implement the MPC algorithm in Python. In this tutorial, we consider MPC for linear dynamical systems and we consider the unconstrained case. Also, since this is the first part of a series of tutorials, we assume that the state vector is completely known. In future tutorials, we will develop MPC algorithms when the state is not known. That is, we will integrate an observer with the MPC algorithms. Also, in future tutorials, we will consider the constrained MPC algorithms and MPC for nonlinear systems. The C++ implementation of the MPC algorithm is given here. The GitHub page with the developed code files is given here. The YouTube page accompanying this tutorial is given below.

The main challenge was how to make a tutorial that was easy for beginners without going immediately into nonlinear and complex optimization worlds, where students immediately get lost and immediately give up on studying MPC. This comment also applies to modern control theory. A number of control scientists publishing papers in Automatica/IEEE TAC simply do not put effort into explaining things such that everyone can understand the basic concepts. There is a trend to make the control theory as complex as possible and as a pure math discipline. I think that was not the vision of the founders of control theory, who were actually engineers solving real-life problems. In fact, control theory is super applicable and relatively easy. The only issue is that one has to conquer math to be able to apply it. Consequently, I start with the MPC formulation for linear systems and I try to stick as much as possible to basic linear algebra.

We explain how to formulate a least-squares cost function, and how to minimize it. The solution can be expressed in a closed form as a solution of a weighted least-squares problem. The input constraints can be implicitly handled by properly selecting weighting matrices. We then explain how to implement this algorithm in Python from scratch and in a disciplined and clean manner (by using Python classes). We test the algorithm on a classical system consisting of two objects connected by springs and dampers. In the second part of this tutorial series, we will consider constrained linear systems. In the third part, we will consider nonlinear smooth systems (the most general formulation). After we complete the Python model predictive control tutorials, we will start a new tutorial series on how to implement the algorithm in C++ by using the Eigen Library.

How to Cite This Document:

“Model Predictive Control (MPC) Tutorial 1: Unconstrained Formulation, Derivation, and Implementation in Python from Scratch”. Technical Report, Number 2, Aleksandar Haber, (2023), Publisher: www.aleksandarhaber.com, Link: https://aleksandarhaber.com/model-predictive-control-mpc-tutorial-1-unconstrained-formulation-derivation-and-implementation-in-python-from-scratch/

When citing this tutorial and the report, include the link.

Copyright Notices and NOT to Be Used for AI Notice

COPYRIGHT NOTICE: THE TEXT, PHOTOS, AND CODES POSTED ON THIS WEBSITE AND ON THIS WEBPAGE ARE THE OWNERSHIP, INTELLECTUAL PROPERTY, AND COPYRIGHTED BY THE AUTHOR: ALEKSANDAR HABER. THE TEXT AND THE CONTENT OF THIS PAGE SHOULD NOT BE PHYSICALLY COPIED, SHOULD NOT BE COPIED ON OTHER WEBSITES, SHOULD NOT BE REPRINTED, SHOULD NOT BE REPOSTED ON OTHER WEBSITES, SHOULD NOT BE USED AS A LECTURE MATERIAL IN UNIVERSITY COURSES, SHOULD NOT BE USED AS LECTURE MATERIAL IN COURSES ORGANIZED BY AND HOSTED ON ONLINE LEARNING PLATFORMS (such as Udemy, Coursera, etc), AND SHOULD NOT BE USED IN COMMERCIAL SETTING. THE TEXT, PHOTOS, AND CODE PRESENTED ON THIS WEBSITE AND WEBPAGE SHOULD NOT BE INCLUDED IN REPORTS, STUDENT PAPERS, SCIENTIFIC PAPERS, OR IN ANY OTHER PRINTED OR A DIGITAL FORM OR A DOCUMENT WITHOUT WRITTEN CONSENT OF THE AUTHOR. A MONEY FEE MIGHT BE REQUIRED TO REPRINT THE MATERIAL POSTED ON THIS WEBSITE: CONTACT THE AUTHOR: ml.mecheng@gmail.com

CODE COPYRIGHT NOTICE AND LICENSE: THE CODE FILES POSTED ON THIS WEBSITE ARE NOT FREE SOFTWARE AND CODE. IF YOU WANT TO USE THIS CODE IN THE COMMERCIAL SETTING OR ACADEMIC SETTING, THAT IS, IF YOU WORK FOR A COMPANY OR IF YOU ARE AN INDEPENDENT CONSULTANT AND IF YOU WANT TO USE THIS CODE OR IF YOU ARE ACADEMIC RESEARCHER OR STUDENT, THEN WITHOUT MY PERMISSION AND WITHOUT PAYING THE PROPER FEE, YOU ARE NOT ALLOWED TO USE THIS CODE. YOU CAN CONTACT ME AT
ml.mecheng@gmail.com
TO INFORM YOURSELF ABOUT THE LICENSE OPTIONS AND FEES FOR USING THIS CODE. ALSO, IT IS NOT ALLOWED TO (1) MODIFY THIS CODE IN ANY WAY WITHOUT MY PERMISSION. (2) INTEGRATE THIS CODE IN OTHER PROJECTS WITHOUT MY PERMISSION. (3) POST THIS CODE ON ANY PRIVATE OR PUBLIC WEBSITES OR CODE REPOSITORIES. DELIBERATE OR INDELIBERATE VIOLATIONS OF THIS LICENSE WILL INDUCE LEGAL ACTIONS AND LAWSUITS.

NOT TO BE USED FOR AI COPYRIGHT NOTICE: The code and text, as well as all other material on this webpage and the YouTube page, should NOT be used to train an AI algorithm or a large language model, or any type of AI or machine learning algorithm used to recognize, interpret, and draw conclusions from text. Also, it is forbidden to crawl this webpage and to extract information for training an AI algorithm of any sort on the basis of the material presented on this webpage.

Model Predictive Control Formulation

We consider the linear system

(1)  

where is the state, is the control input, is the output that we want to control, and and are system matrices. In the current problem formulation, the output is not necessarily the observed output, that is, it is not necessarily equal to the measured output.

In our problem formulation is actually a set of state variables that should follow a desired reference trajectory. Since this is the first part of the tutorial series on Model Predictive Control (MPC), we will assume that the state vector is perfectly known. That is, we assume that we have perfectly reconstructed the state vector. In future tutorials, we will consider the case when the state vector is not directly observable. In that case, we will couple a state reconstructor (also known as an observer) with the MPC algorithm.

Next, we need to introduce the following notation which is also illustrated in the figure below.

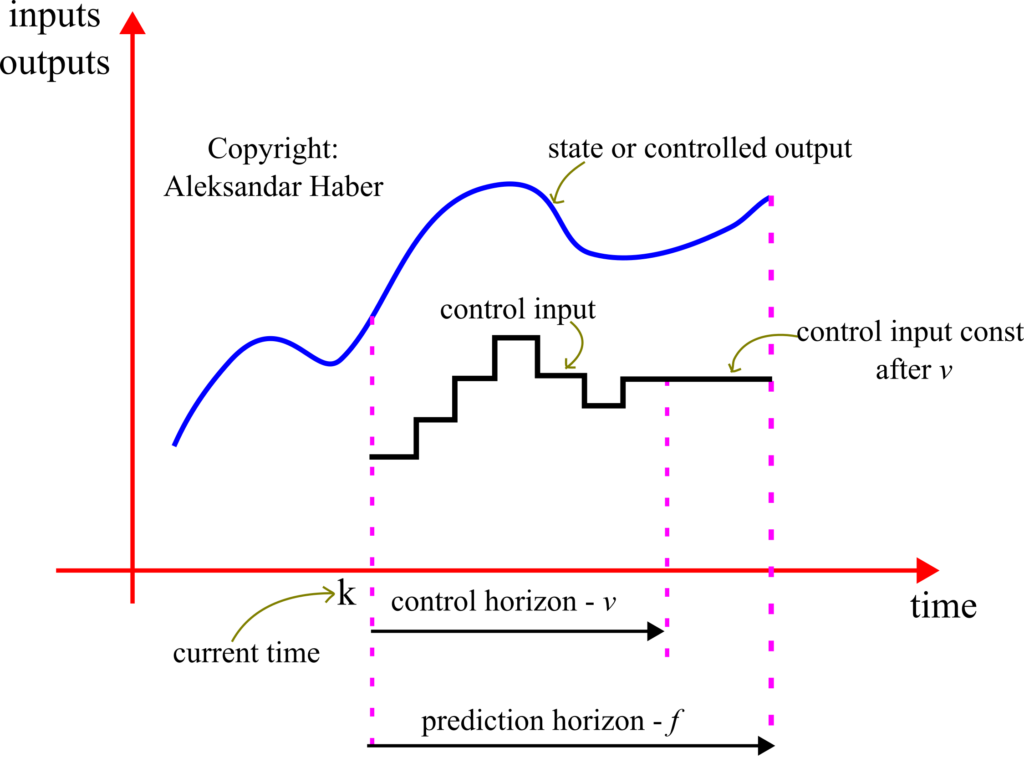
• The length of the prediction horizon is denoted by 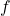. This is the future prediction horizon over which we will predict the state trajectory behavior. The prediction horizon is selected by the user and in some cases, can also be seen as a tuning parameter.
• The length of the control horizon is denoted by . This is the future control horizon over which we allow for the control inputs to change. We introduce the following limitation 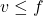. After the control horizon, the control input is kept constant and equal to the last value in the control horizon (this will become clearer in the sequel). The control horizon is selected by the user and in some cases, can also be seen as a tuning parameter.
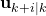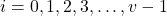• , is the control input at the time step 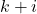and that is computed at the time step . This control input is determined as the solution to the MPC problem. Note over here that the control input vector only varies until 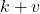, after that it is constant and equal to 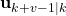(this will be clarified in the sequel).
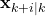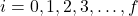• , is the prediction of the state vector at the time instant 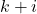and that is made at the time instant .
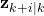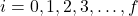• , is the prediction of the output vector at the time instant 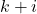and that is made at the time instant .

The goal of the model predictive controller is to determine a set of control inputs , at the time instant , that will make the output of the system , to follow a prescribed output trajectory (desired control trajectory) over the prediction horizon. This is done by using the knowledge of the current state , and the system model matrices and to predict the output trajectory , , and then to minimize the difference between the desired and predicted trajectories. This will become clearer in the sequel.

Let us assume that we are currently at the time instant and that we want to make state and output predictions up to the time instant . Also, let us assume that the state at the time instant is perfectly known. That is, we assume that is known. From (1) we have for the time instant

(2)  

Then, by using the last equation, we can write the state and output predictions for the time instant

(3)  

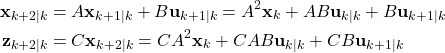
By using the same principle, for the time instant , we can write

(4)  

The last equation can be written in the compact form

(5)  

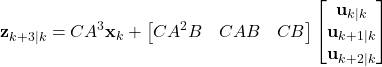
By continuing with this procedure until the time index ( is the control horizon), we obtain

(6)  

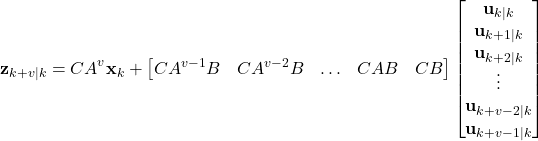
The index is important mainly because after this index, we have

(7)  

This is a constraint that we impose on our controller. By using this equation, we have for the time index

(8)  

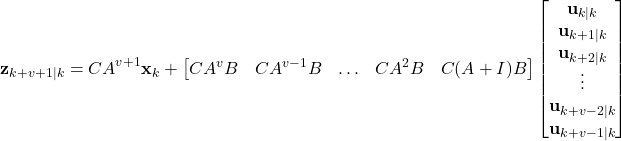
By using the same procedure and by shifting the time index, we obtain the prediction for the final step

(9)  

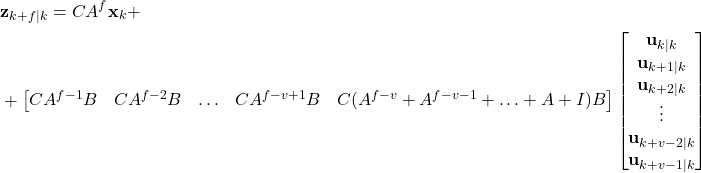
The last equation can be written compactly

(10)  

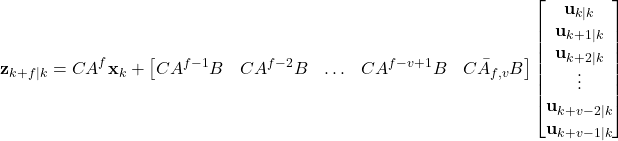
where

(11)  

In the general case, we introduce the following notation for

(12)  

By combining all the prediction equations in a single equation, we obtain

(13)  

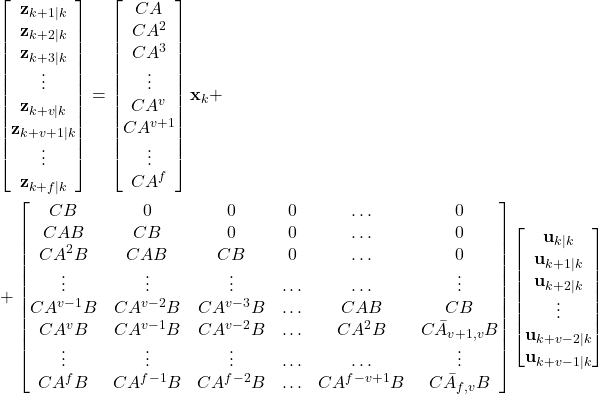
where is defined in (12) for and and is defined (11).

The last equation can be written compactly as follows

(14)  

where

(15)  

The model predictive control problem can be formulated as follows. The goal is to track a reference output trajectory. Let these desired outputs be denoted by

(16)  

where the superscript “d” means that the outputs are desired outputs. Let the vector be defined by

(17)  

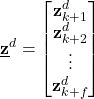
A natural way of formulating the model predictive control problem is to determine the vector of control inputs , defined in (15), such that the following cost function is minimized

(18)  

where is defined in (15). However, the issue with this approach is that we do not have control on the magnitude of control inputs . The control inputs can be extremely large, and thus impossible to be applied in practice, or they can lead to actuator saturation that can lead to devastating effects in a feedback control loop. Consequently, we need to introduce a penalty on the control inputs in the cost function. Furthermore, we need to introduce weights in the cost function (18) to have better control of the convergence of the algorithm.

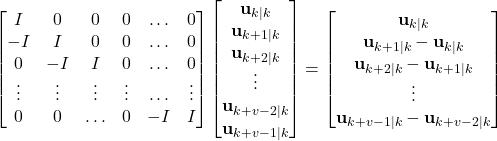
The part of the cost function that will penalize the inputs has the following form

(19)  

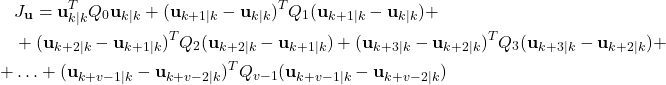
where , are symmetric weighting matrices selected by the user. The idea for introducing this cost function is to penalize the magnitude of the first applied control input and the difference between the subsequent control inputs. The weighting matrices , , are used to penalize these inputs. Next, we need to write the cost function (19) in the vector form. We can do that by introducing the following expression

(20)  

The last expression can be written compactly as

(21)  

where

(22)  

and where is defined in (15). We can write the cost function (19) as follows

(23)  

where

(24)  

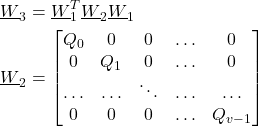
The matrix is a block diagonal matrix with the block matrices , , on the main block diagonal.

Next, we introduce the part of the cost function that corresponds to the tracking error:

(25)  

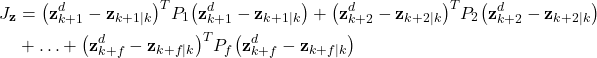
By introducing

(26)  

where , are the symmetric weighting matrices that should be selected by the user. By using (14), (15), (17), and (26), and we can write the cost function as follows

(27)  

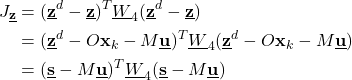
where

(28)  

This part of the cost function penalizes the difference between the desired trajectory and the controlled trajectory. Let us analyze the part of the cost function (27). Since it is assumed that the state vector is known, and the desired trajectory vector is given, the vector defined in (28) can be computed. Our goal is to determine the vector . This vector will be determined by minimizing the cost function

(29)  

By substituting (23) and (27) in (29), we obtain

(30)  

Next, we need to minimize the cost function (30). To do that, let us write

(31)  

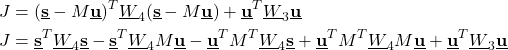
Next, we need to minimize the expression . We can do that by recalling formulas for the derivative of scalar functions with respect to vectors. Let, be a vector and a constant vector. Also, let be a constant symmetric matrix. Then, from Chapter 2.4 of the Matrix Cook Book, we have (see equations (69) and (81) from that amazing book)

(32)  

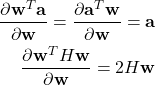
Then, by using these two equations, we can differentiate all the terms in (31):

(33)  

(34)  

(35)  

(36)  

(37)  

By using (33)-(37), we can compute the derivative of the cost function defined in (31)

(38)  

To find the minimum of the cost function with respect to , we set

(39)  

From where we obtain

(40)  

(41)  

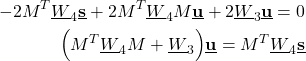
From the last equation, we obtain the solution of the model predictive control problem:

(42)  

It can be shown that this is the solution that actually minimizes the cost function . This can be shown by computing a Hessian matrix and showing that the Hessian matrix is positive definite. The solution can be expressed as

(43)  

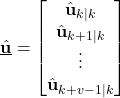
We only need the first entry, that is . We apply this input to the system, and we then wait for the time instant , observe the state , and form another cost function for the time instant , compute its solution, and apply to the system, and repeat the procedure for the time instant

The derived model predictive control algorithm can be summarized as follows.

STEP 1: At the time instant , on the basis of the known state vector , and the system matrices , form the lifted matrices and compute the solution given by (42).

STEP 2: Extract the first entry of this solution and apply it to the system.

STEP 3: Wait for the system to respond and obtain the state measurement . Shift the time index to and go to STEP 1.

Model for Testing the Model Predictive Controller

We consider a mass-spring damper system as a test case for the model predictive controller. The state-space model of this system is derived in our previous tutorial which can be found here. The model is shown in the figure below.

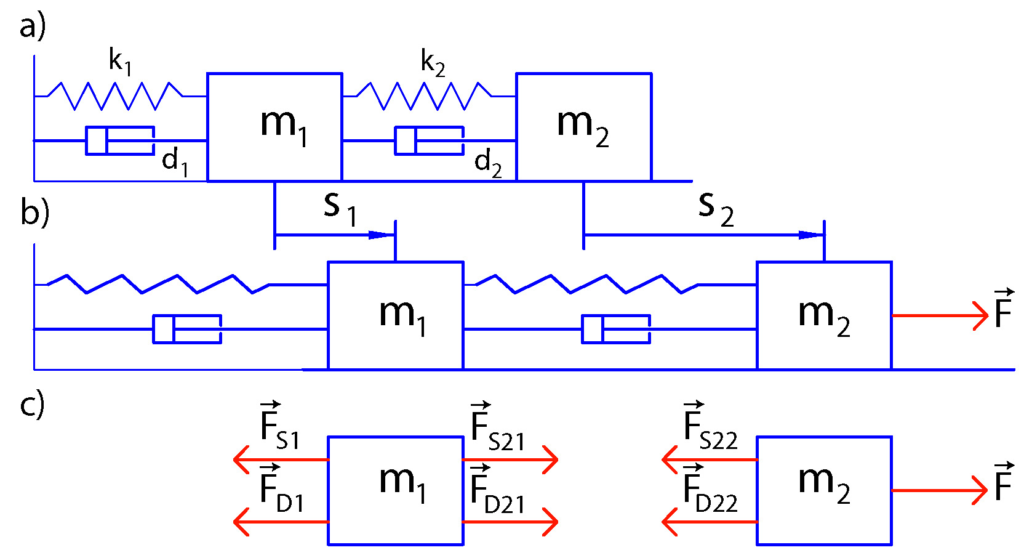
The state-space model has the following form:

(44)  

(45)  

The next step is to transform the state-space model (44)-(45) in the discrete-time domain. Due to its simplicity and good stability properties, we use the Backward Euler method to perform the discretization. This method approximates the state derivative as follows

(46)  

where is the discretization constant. For simplicity, we assumed that the discrete-time index of the input is . We can also assume that the discrete-time index of input is if we want. However, then, when simulating the system dynamics we will start from . From the last equation, we have

(47)  

where and . On the other hand, the output equation remains unchanged

(48)  

The step response of the system is shown below (the codes are given in the section on Python implementation).

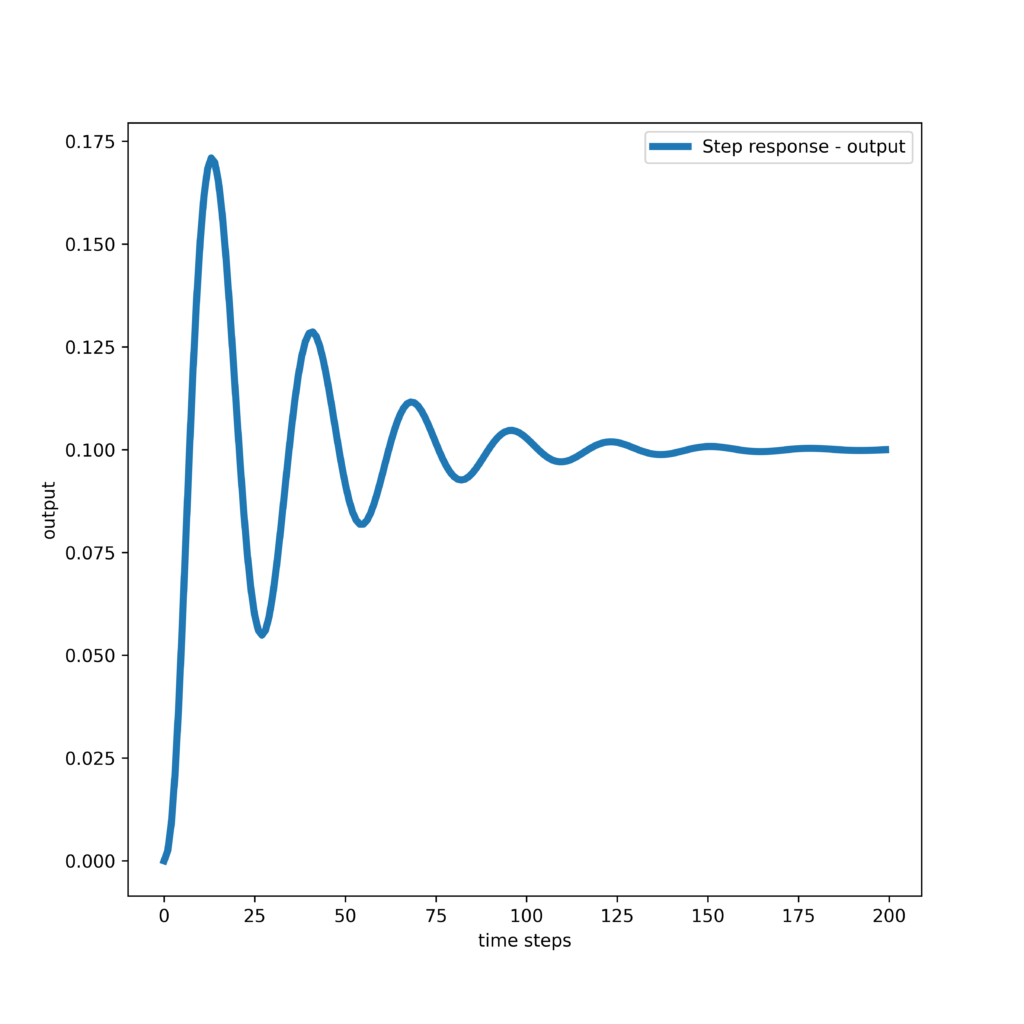
Numerical Tests of Applying the Model Predictive Controller

Here, we present numerical tests of applying the model predictive controller. The Python codes used to generate these results are presented in the next section.

First, we present the results obtained by tracking a step trajectory. The response of the controller and control inputs are shown in the two graphs given below.

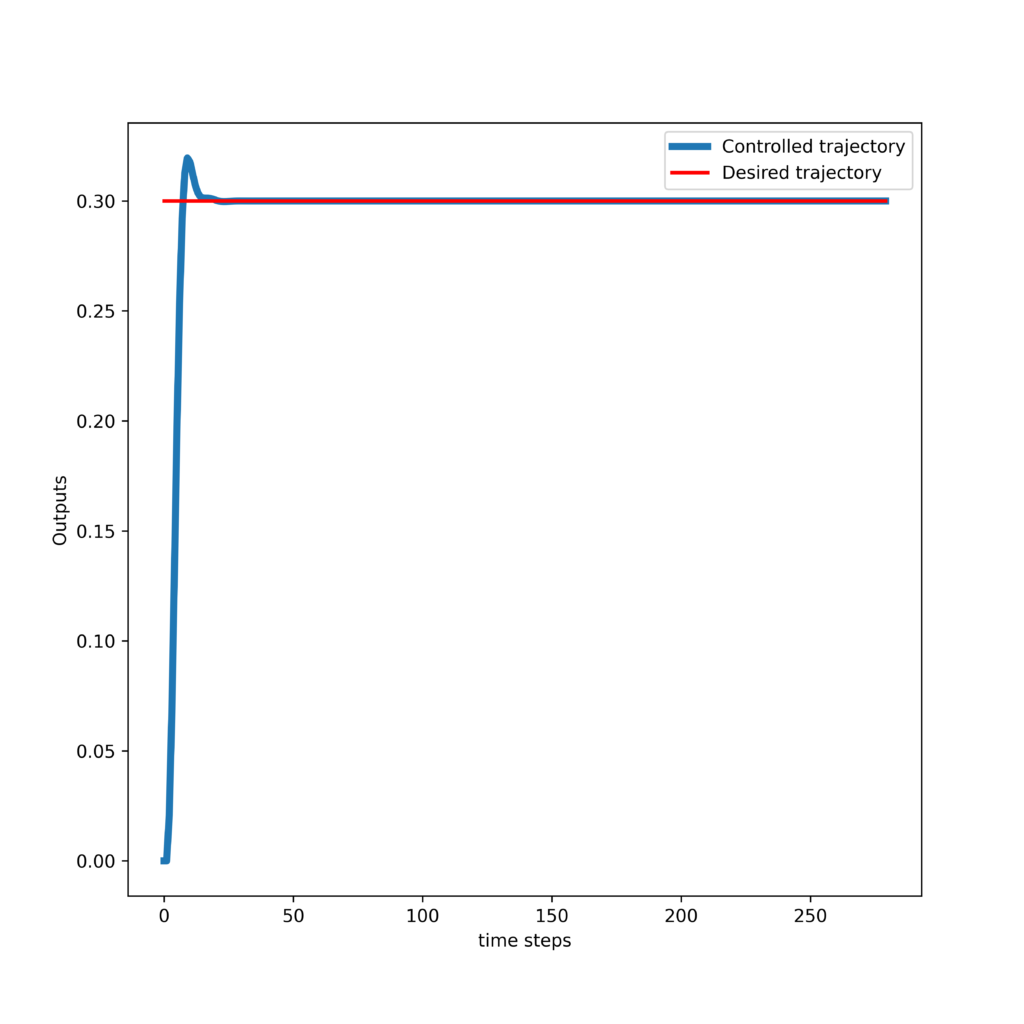
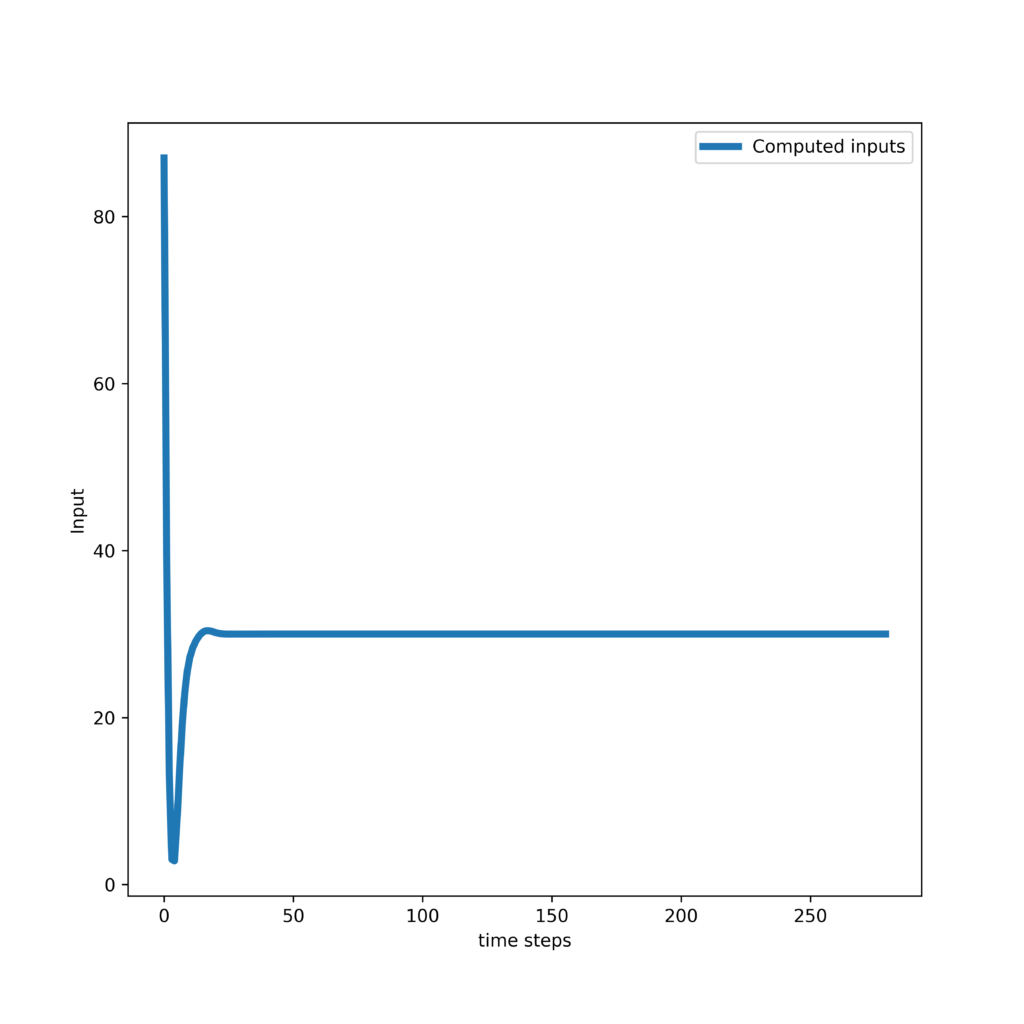
Secondly, we present the results obtained by tracking a pulse trajectory. The response of the controller and control inputs are shown in the two graphs given below.

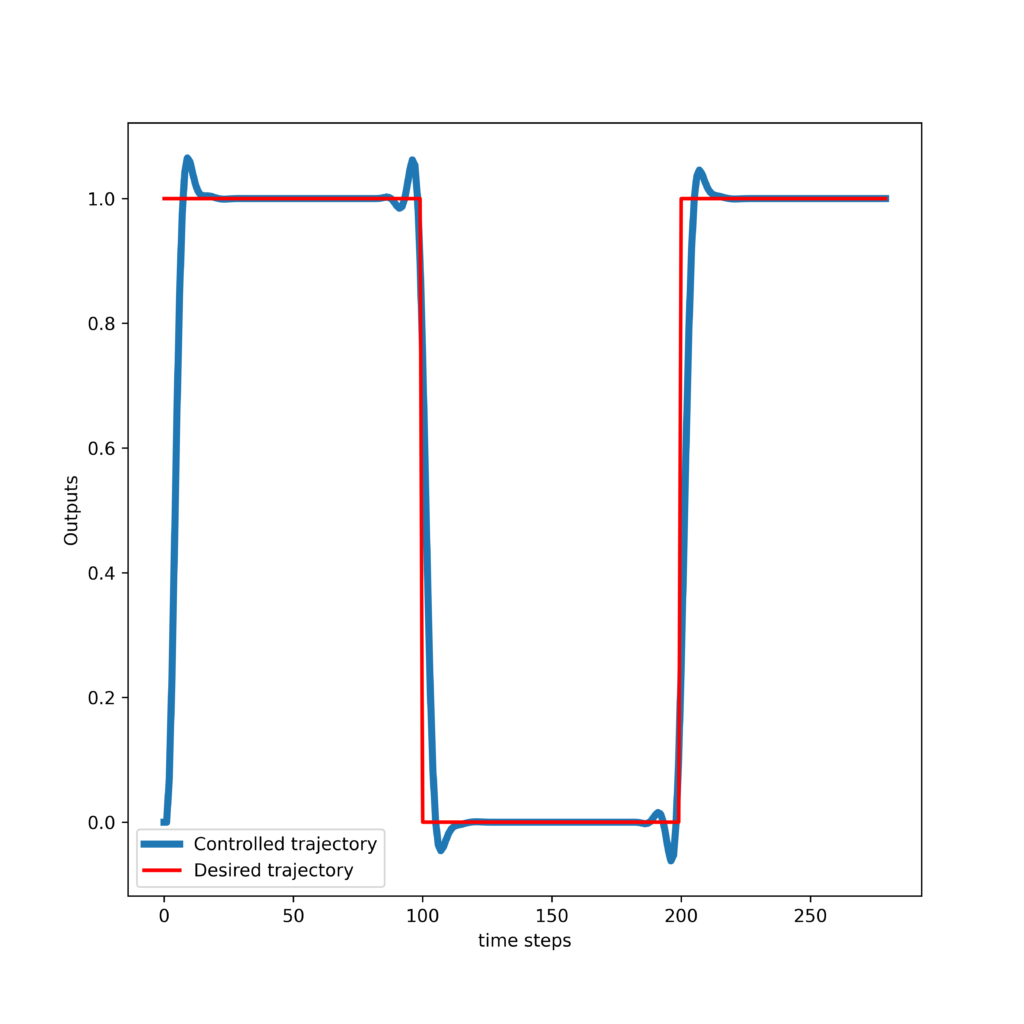
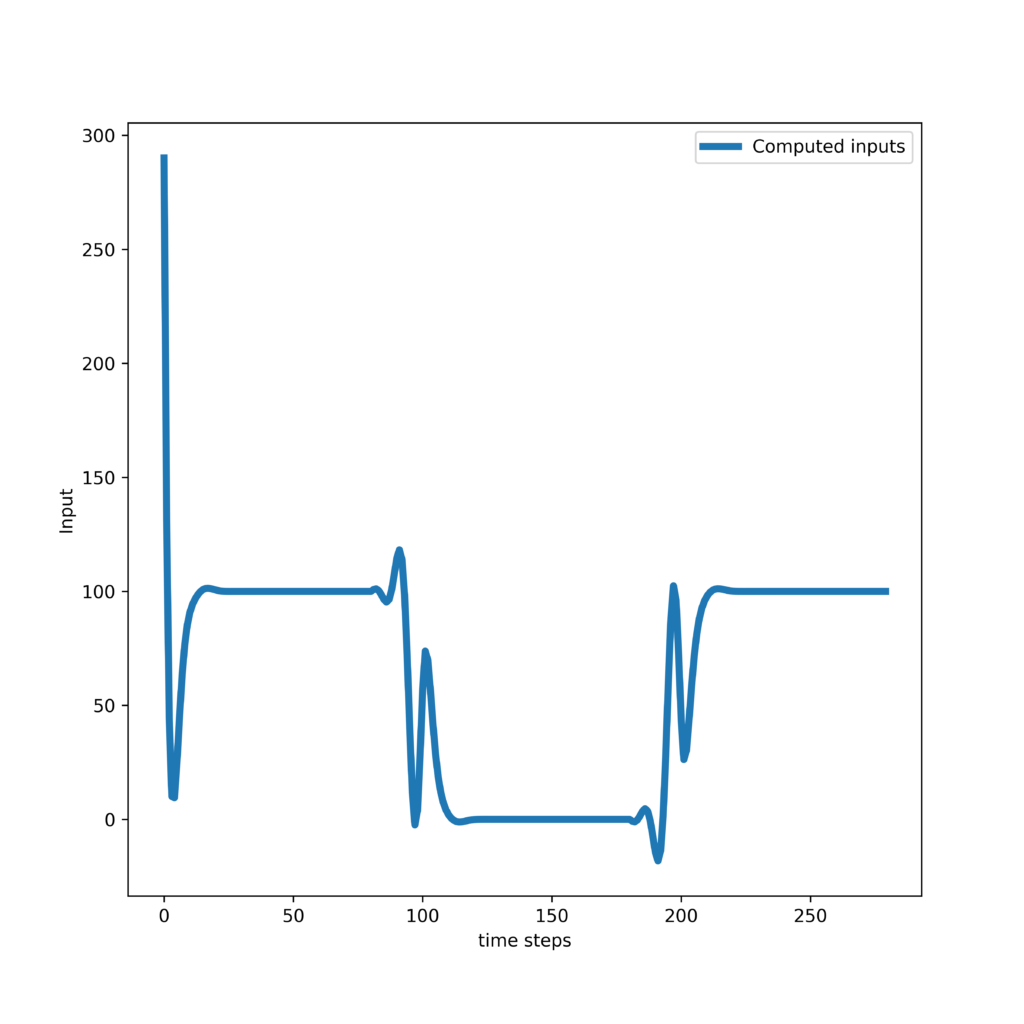
Thirdly, we present the results obtained by tracking an exponential trajectory. The response of the controller and control inputs are shown in the two graphs given below.

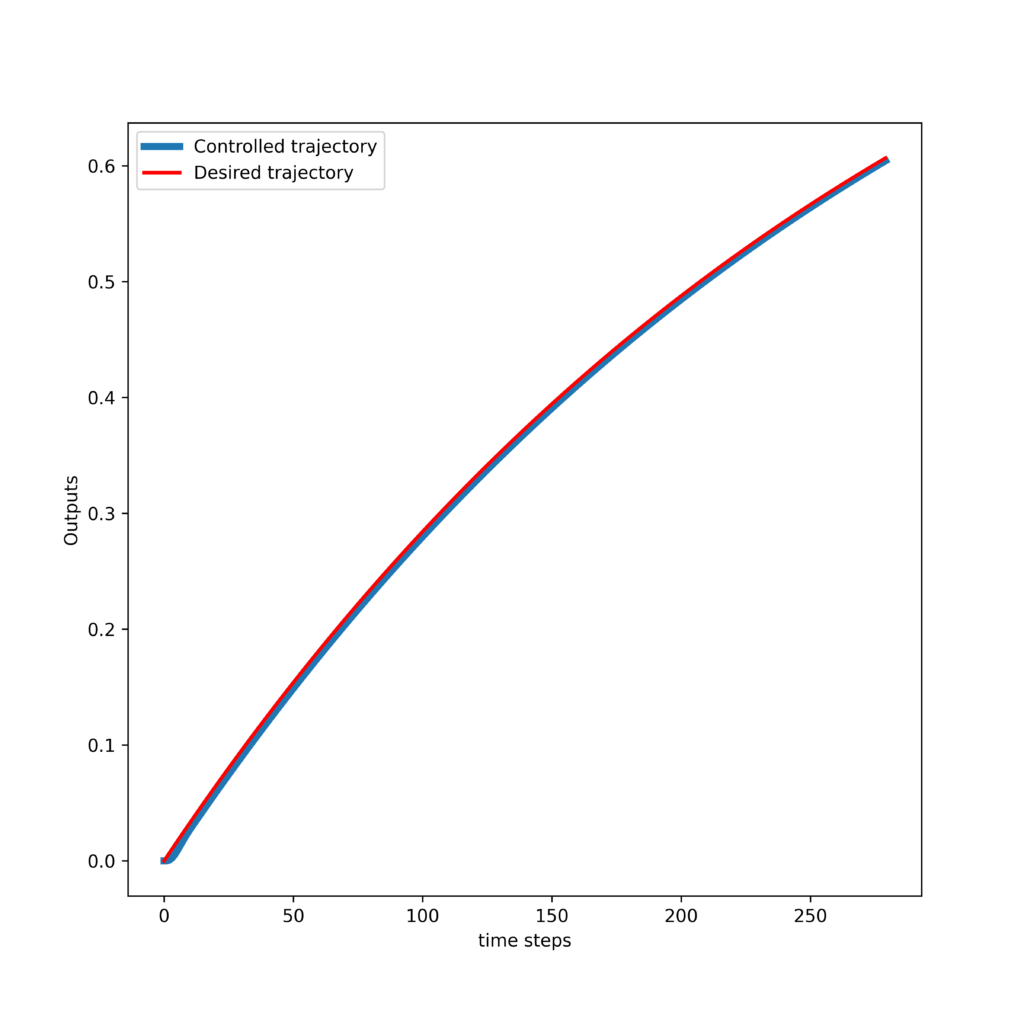
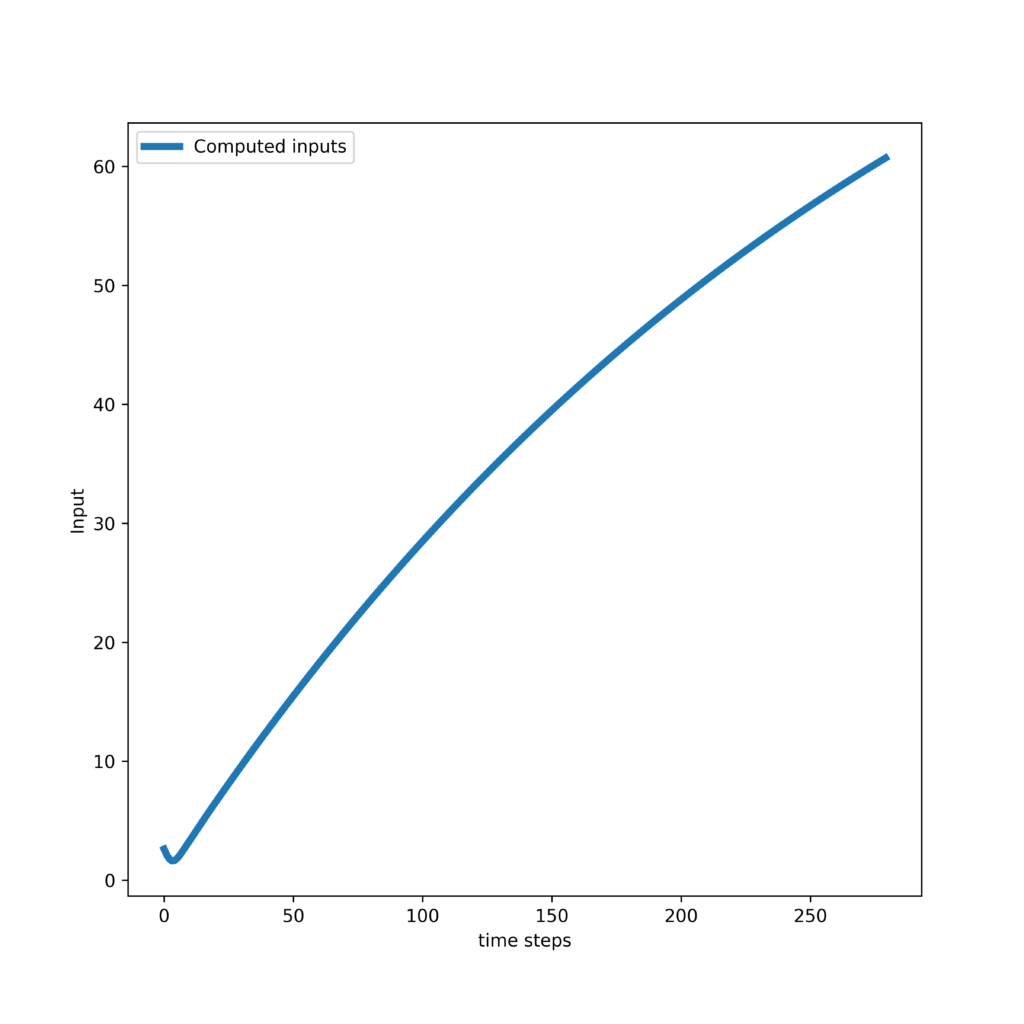
Python Implementation of Model Predictive Controller

All the codes presented here are posted on the GitHub page. The following code presents an implementation of a Python class that implements the model predictive controller.

import numpy as np 

class ModelPredictiveControl(object):
    
    # A,B,C - system matrices
    # f -  prediction horizon
    # v  - control horizon
    # W3 - input weight matrix
    # W4 - prediction weight matrix
    # x0 - initial state of the system
    # desiredControlTrajectoryTotal - total desired control trajectory
    #                               later on, we will take segments of this
    #                               desired state trajectory
    
    def __init__(self,A,B,C,f,v,W3,W4,x0,desiredControlTrajectoryTotal):
        
        # initialize variables
        self.A=A 
        self.B=B
        self.C=C
        self.f=f
        self.v=v
        self.W3=W3 
        self.W4=W4
        self.desiredControlTrajectoryTotal=desiredControlTrajectoryTotal
        
        # dimensions of the matrices
        
        self.n=A.shape[0]
        self.r=C.shape[0]
        self.m=B.shape[1]        
                
               
        # this variable is used to track the current time step k of the controller
        # after every calculation of the control inpu, this variables is incremented for +1 
        self.currentTimeStep=0
        
        # we store the state vectors of the controlled state trajectory
        self.states=[]
        self.states.append(x0)
        
        # we store the computed inputs 
        self.inputs=[]
        
        # we store the output vectors of the controlled state trajectory
        self.outputs=[]
        self.outputs.append(np.matmul(C,x0))
        
        # form the lifted system matrices and vectors
        # the gain matrix is used to compute the solution 
        # here we pre-compute it to save computational time
        self.O, self.M, self.gainMatrix = self.formLiftedMatrices()
        
    
    # this function forms the lifted matrices O and M, as well as the 
    # the gain matrix of the control algorithm
    # and returns them 
    def formLiftedMatrices(self):
        f=self.f
        v=self.v
        r=self.r
        n=self.n
        m=self.m
        A=self.A
        B=self.B
        C=self.C
        
        # lifted matrix O
        O=np.zeros(shape=(f*r,n))

        for i in range(f):
            if (i == 0):
                powA=A;
            else:
                powA=np.matmul(powA,A)
            O[i*r:(i+1)*r,:]=np.matmul(C,powA)

        # lifted matrix M        
        M=np.zeros(shape=(f*r,v*m))
    
        for i in range(f):
            # until the control horizon
            if (i<v):
                for j in range(i+1):
                    if (j == 0):
                        powA=np.eye(n,n);
                    else:
                        powA=np.matmul(powA,A)
                    M[i*r:(i+1)*r,(i-j)*m:(i-j+1)*m]=np.matmul(C,np.matmul(powA,B))
            
            # from control horizon until the prediction horizon
            else:
                for j in range(v):
                    # here we form the last entry
                    if j==0:
                        sumLast=np.zeros(shape=(n,n))
                        for s in range(i-v+2):
                            if (s == 0):
                                powA=np.eye(n,n);
                            else:
                                powA=np.matmul(powA,A)
                            sumLast=sumLast+powA
                        M[i*r:(i+1)*r,(v-1)*m:(v)*m]=np.matmul(C,np.matmul(sumLast,B))
                    else:
                        powA=np.matmul(powA,A)
                        M[i*r:(i+1)*r,(v-1-j)*m:(v-j)*m]=np.matmul(C,np.matmul(powA,B))
        
        
        tmp1=np.matmul(M.T,np.matmul(self.W4,M))
        tmp2=np.linalg.inv(tmp1+self.W3)
        gainMatrix=np.matmul(tmp2,np.matmul(M.T,self.W4))
        
        
        return O,M,gainMatrix
    
    # this function propagates the dynamics
    # x_{k+1}=Ax_{k}+Bu_{k}
    
    def propagateDynamics(self,controlInput,state):

        xkp1=np.zeros(shape=(self.n,1))
        yk=np.zeros(shape=(self.r,1))
        xkp1=np.matmul(self.A,state)+np.matmul(self.B,controlInput)
        yk=np.matmul(self.C,state)
        
        return xkp1,yk
        
    # this function computes the control inputs, applies them to the system 
    # by calling the propagateDynamics() function and appends the lists
    # that store the inputs, outputs, states
    def computeControlInputs(self):
                
        # extract the segment of the desired control trajectory
        desiredControlTrajectory=self.desiredControlTrajectoryTotal[self.currentTimeStep:self.currentTimeStep+self.f,:]

        # compute the vector s
        vectorS=desiredControlTrajectory-np.matmul(self.O,self.states[self.currentTimeStep])
       
        # compute the control sequence
        inputSequenceComputed=np.matmul(self.gainMatrix,vectorS)
        inputApplied=np.zeros(shape=(1,1))
        inputApplied[0,0]=inputSequenceComputed[0,0]
        
        # compute the next state and output
        state_kp1,output_k=self.propagateDynamics(inputApplied,self.states[self.currentTimeStep])
        
        # append the lists
        self.states.append(state_kp1)
        self.outputs.append(output_k)
        self.inputs.append(inputApplied)
        # increment the time step
        self.currentTimeStep=self.currentTimeStep+1
        

The definition is straightforward and easy to understand. This class should be saved in the file called “ModelPredictiveControl.py”. Next, we need a helper function for simulating the system response. This function is given below.

###############################################################################
# This function simulates an open loop state-space model:
# x_{k+1} = A x_{k} + B u_{k}
# y_{k}   = C x_{k}
# starting from an initial condition x_{0}

# Input parameters:
# A,B,C - system matrices 
# U - the input matrix, its dimensions are \in \mathbb{R}^{m \times simSteps},  where m is the input vector dimension
# Output parameters:
# Y - simulated output - dimensions \in \mathbb{R}^{r \times simSteps}, where r is the output vector dimension
# X - simulated state - dimensions  \in \mathbb{R}^{n \times simSteps}, where n is the state vector dimension

def systemSimulate(A,B,C,U,x0):
    import numpy as np
    simTime=U.shape[1]
    n=A.shape[0]
    r=C.shape[0]
    X=np.zeros(shape=(n,simTime+1))
    Y=np.zeros(shape=(r,simTime))
    for i in range(0,simTime):
        if i==0:
            X[:,[i]]=x0
            Y[:,[i]]=np.matmul(C,x0)
            X[:,[i+1]]=np.matmul(A,x0)+np.matmul(B,U[:,[i]])
        else:
            Y[:,[i]]=np.matmul(C,X[:,[i]])
            X[:,[i+1]]=np.matmul(A,X[:,[i]])+np.matmul(B,U[:,[i]])
    
    return Y,X

###############################################################################
# end of function
###############################################################################

This helper function should be saved in the file “functionMPC.py”. Finally, below we present the driver code for the model predictive controller.

import numpy as np
import matplotlib.pyplot as plt

from functionMPC import systemSimulate
from ModelPredictiveControl import ModelPredictiveControl


###############################################################################
#  Define the MPC algorithm parameters
###############################################################################
# prediction horizon
f= 20
# control horizon 
v=20

###############################################################################
# end of MPC parameter definitions
###############################################################################


###############################################################################
# Define the model
###############################################################################

# masses, spring and damper constants
m1=2  ; m2=2   ; k1=100  ; k2=200 ; d1=1  ; d2=5; 
# define the continuous-time system matrices
Ac=np.matrix([[0, 1, 0, 0],
              [-(k1+k2)/m1 ,  -(d1+d2)/m1 , k2/m1 , d2/m1 ],
              [0 , 0 ,  0 , 1], 
              [k2/m2,  d2/m2, -k2/m2, -d2/m2]])
Bc=np.matrix([[0],[0],[0],[1/m2]])
Cc=np.matrix([[1, 0, 0, 0]])

r=1; m=1 # number of inputs and outputs
n= 4 # state dimension


###############################################################################
# end of model definition
###############################################################################

###############################################################################
# discretize and simulate the system step response
###############################################################################

# discretization constant
sampling=0.05

# model discretization
I=np.identity(Ac.shape[0]) # this is an identity matrix
A=np.linalg.inv(I-sampling*Ac)
B=A*sampling*Bc
C=Cc

# check the eigenvalues
eigen_A=np.linalg.eig(Ac)[0]
eigen_Aid=np.linalg.eig(A)[0]

timeSampleTest=200

# compute the system's step response
inputTest=10*np.ones((1,timeSampleTest))
x0test=np.zeros(shape=(4,1))


# simulate the discrete-time system 
Ytest, Xtest=systemSimulate(A,B,C,inputTest,x0test)


plt.figure(figsize=(8,8))
plt.plot(Ytest[0,:],linewidth=4, label='Step response - output')
plt.xlabel('time steps')
plt.ylabel('output')
plt.legend()
plt.savefig('stepResponse.png',dpi=600)
plt.show()

###############################################################################
# end of step response
###############################################################################

###############################################################################
# form the weighting matrices
###############################################################################

# W1 matrix
W1=np.zeros(shape=(v*m,v*m))

for i in range(v):
    if (i==0):
        W1[i*m:(i+1)*m,i*m:(i+1)*m]=np.eye(m,m)
    else:
        W1[i*m:(i+1)*m,i*m:(i+1)*m]=np.eye(m,m)
        W1[i*m:(i+1)*m,(i-1)*m:(i)*m]=-np.eye(m,m)

# W2 matrix
Q0=0.0000000011
Qother=0.0001

W2=np.zeros(shape=(v*m,v*m))

for i in range(v):
    if (i==0):
        W2[i*m:(i+1)*m,i*m:(i+1)*m]=Q0
    else:
        W2[i*m:(i+1)*m,i*m:(i+1)*m]=Qother

# W3 matrix        
W3=np.matmul(W1.T,np.matmul(W2,W1))

# W4 matrix
W4=np.zeros(shape=(f*r,f*r))

# in the general case, this constant should be a matrix
predWeight=10

for i in range(f):
    W4[i*r:(i+1)*r,i*r:(i+1)*r]=predWeight
###############################################################################
# end of step response
###############################################################################

###############################################################################
# Define the reference trajectory 
###############################################################################

timeSteps=300

# here you need to comment/uncomment the trajectory that you want to use

# exponential trajectory
timeVector=np.linspace(0,100,timeSteps)

desiredTrajectory=np.ones(timeSteps)-np.exp(-0.01*timeVector)
desiredTrajectory=np.reshape(desiredTrajectory,(timeSteps,1))

# pulse trajectory
desiredTrajectory=np.zeros(shape=(timeSteps,1))
desiredTrajectory[0:100,:]=np.ones((100,1))
desiredTrajectory[200:,:]=np.ones((100,1))

# step trajectory
timeSteps=300
desiredTrajectory=0.3*np.ones(shape=(timeSteps,1))

###############################################################################
# end of definition of the reference trajectory 
###############################################################################

###############################################################################
# Simulate the MPC algorithm and plot the results
###############################################################################

# set the initial state
x0=x0test

# create the MPC object

mpc=ModelPredictiveControl(A,B,C,f,v,W3,W4,x0,desiredTrajectory)

# simulate the controller

for i in range(timeSteps-f):
    mpc.computeControlInputs()
    
    

# extract the state estimates in order to plot the results
desiredTrajectoryList=[]
controlledTrajectoryList=[]
controlInputList=[]
for j in np.arange(timeSteps-f):
    controlledTrajectoryList.append(mpc.outputs[j][0,0])
    desiredTrajectoryList.append(desiredTrajectory[j,0])
    controlInputList.append(mpc.inputs[j][0,0])

# plot the results
    
plt.figure(figsize=(8,8))
plt.plot(controlledTrajectoryList,linewidth=4, label='Controlled trajectory')
plt.plot(desiredTrajectoryList,'r', linewidth=2, label='Desired trajectory')
plt.xlabel('time steps')
plt.ylabel('Outputs')
plt.legend()
plt.savefig('controlledOutputs.png',dpi=600)
plt.show()


plt.figure(figsize=(8,8))
plt.plot(controlInputList,linewidth=4, label='Computed inputs')
plt.xlabel('time steps')
plt.ylabel('Input')
plt.legend()
plt.savefig('inputs.png',dpi=600)
plt.show()