Math/Control Systems Tutorial – Partial Fraction Expansion with MATLAB – Part III – Fusion of Engineering, Control, Coding, Machine Learning, and Science

This is the final lecture on partial fraction expansion. The first and second parts of this lecture can be found here and here. The video accompanying this post can be found here:

This lecture covers the case when the rational (transfer) function has repeated poles (poles are roots of the expression in the denominator). Let the poles of the transfer function $W(s)$ be $p_{1},p_{2},\ldots, p_{n}$ . We assume that the pole $p_{1}$ is repeated three times. Then, the partial fraction expansion of $W(s)$ becomes:

(1) $\begin{align*}W(s)=\frac{C_{1}}{s-p_{1}}+\frac{C_{2}}{(s-p_{1})^2}+\frac{C_{3}}{(s-p_{1})^3}+\frac{C_{4}}{s-p_{2}}+\ldots+\frac{C_{n}}{s-p_{n}}\end{align*}$

Our goal is to find the constants $C_{1},C_{2},\ldots, C_{n}$ .
If we multiply the last expression with (s-p_{1})^{3}, we obtain

(2) $\begin{align*}& W(s)(s-p_{1})^{3}=C_{1}(s-p_{1})^{2}+C_{2}(s-p_{1})+C_{3}+\frac{C_{4}(s-p_{1})^{3}}{s-p_{2}}+\ldots+\notag \\& +\frac{C_{n}(s-p_{1})^{3}}{s-p_{n}}\end{align*}$

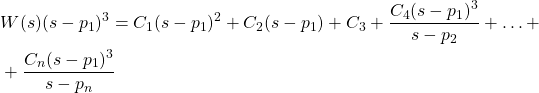
From the last equation, we immediately obtain

(3) $\begin{align*}C_{3}=W(s)(s-p_{1})^{3}\vert_{s=p_{1}}\end{align*}$

Taking the first derivative of (2), we obtain:

(4) $\begin{align*}&\frac{d}{ds}\Big(W(s)(s-p_{1})^{3}\Big)=2C_{1}(s-p_{1})+C_{2}\notag\\&+\frac{d}{ds}\big( \frac{C_{4}(s-p_{1})^{3}}{s-p_{2}}+\ldots+\frac{C_{n}(s-p_{1})^{3}}{s-p_{n}}\big)\end{align*}$

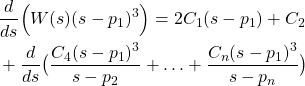
If we evaluate the last expression for $s=p_{1}$ , the first term on the right-hand-side is zero. Also, the derivative of the expression in the brackets is zero becasue of the third power of $(s-p_{1})$ that multiplies all the terms. Consequently, we obtain

(5) $\begin{align*}\frac{d}{ds}\Big(W(s)(s-p_{1})^{3}\Big)\vert_{s=p_{1}}=C_{2}\end{align*}$

By taking the derivative of (4), we obtain

(6) $\begin{align*}&\frac{d^{2}}{ds^{2}}\Big(W(s)(s-p_{1})^{3}\Big)=2C_{1}+\frac{d^{2}}{ds^{2}}\big( \frac{C_{4}(s-p_{1})^{3}}{s-p_{2}}+\ldots+\frac{C_{n}(s-p_{1})^{3}}{s-p_{n}}\big)\end{align*}$

Again, the second term on the right-hand-side of the last expression will be zero due to the term $(s-p_{1})^{3}$ multiplying all the terms. From the last equation, we obtain

(7) $\begin{align*}\frac{1}{2}\frac{d^{2}}{ds^{2}}\Big(W(s)(s-p_{1})^{3}\Big)\vert_{s=p_{1}}=C_{1}\end{align*}$

This procedure can be generalized when a transfer function has $k$ repeated poles. The coefficients then become

(8) $\begin{align*}C_{k-i}=\frac{1}{i!}\frac{d^{i}}{ds^{i}}\Big(W(s)(s-p_{1})^{k}\Big)\vert_{s=p_{1}}, i=0,1,\ldots, k-1\end{align*}$

The remaining coefficients corresponding to distinct poles are computed using previously explained approaches that can be found here and here.
Let us now illustrate these derivations with an example.

Example 1: Find the inverse Laplace transform of the function

(9) $\begin{align*}W(s)=\frac{s+1}{(s+2)(s+3)^{3}}\end{align*}$

The partial fraction expansion is

(10) $\begin{align*}W(s)=\frac{C_{1}}{s+3}+\frac{C_{2}}{(s+3)^{2}}+\frac{C_{3}}{(s+3)^{3}}+\frac{C_{4}}{s+2}\end{align*}$

The constant $C_{3}$ is

(11) $\begin{align*}C_{3}=\frac{s+1}{s+2}\vert_{s=-3}=2\end{align*}$

The constant $C_{2}$ is

(12) $\begin{align*}C_{2}=\frac{d}{ds}\Big(\frac{s+1}{s+2}\Big)\vert_{s=-3}=\frac{1}{(s+2)^{2}}\vert_{s=-3}=1\end{align*}$

The constant $C_{1}$ is

(13) $\begin{align*}C_{1}=\frac{1}{2}\frac{d^{2}}{ds^{2}}\Big(\frac{s+1}{s+2}\Big)\vert_{s=-3}=\frac{1}{(s+2)^{2}}\vert_{s=-3}=-\frac{1}{(s+3)^{3}}=1\end{align*}$

The constant $C_{4}$ is

(14) $\begin{align*}C_{4}=\frac{s+1}{(s+3)^{3}}\vert_{s=-2}=-1\end{align*}$

Finally, we have

(15) $\begin{align*}W(s)=\frac{1}{s+3}+\frac{1}{(s+3)^{2}}+\frac{2}{(s+3)^{3}}+\frac{-1}{s+2}\end{align*}$

The inverse Laplace transform is given by

(16) $\begin{align*}w(t)=\Big(e^{-3t}+e^{-3t}t+e^{-3t}t^{2}-e^{-2t}\Big)h(t)\end{align*}$

where $h(t)$ is the Heaviside step function.

The MATLAB code for solving this problem is given below

clc
syms s
  
F=(s+1)/((s+2)*(s+3)^3)
  
Factorized=partfrac(F)
  
ilaplace(Factorized)

The output is

F =
 
(s + 1)/((s + 2)*(s + 3)^3)
 
 
Factorized =
 
1/(s + 3) - 1/(s + 2) + 1/(s + 3)^2 + 2/(s + 3)^3
 
 
ans =
 
exp(-3*t) - exp(-2*t) + t*exp(-3*t) + t^2*exp(-3*t)

admin

You might also like

Pull-up/pull-down resistors and interrupts – Raspberry Pi

Calculate Eigenvalues and Eigenvectors of Matrices by Hand

Basics of Fanuc Motion Instructions