Math/Control Systems Tutorial – Partial Fraction Expansion with MATLAB – Part II – Fusion of Engineering, Control, Coding, Machine Learning, and Science

We continue with the explanation of the partial fraction expansion. In the first part of this post, which can be accessed here, we explained the partial fraction expansion when our rational function (transfer) function has distinct roots. Also, we gave an example of a transfer function with real roots. Let us now focus on an example of distinct but complex roots. Such examples often appear in practice, and we need to dedicate special attention to them. The video accompanying this post can be found here:

Example 1: Compute the step response of the system given by an ODE:

(1) $\begin{align*}\ddot{y}+\dot{y}+y=u\end{align*}$

Assume zero initial conditions.
Solution: We use the Laplace transform method to solve this problem. Taking the Laplace transform of both sides of (1), we obtain:

(2) $\begin{align*}s^2 Y(s) -sy(0)-\dot{y}(0)+sY(s)-y(0)+Y(s)=U(s)\end{align*}$

where $Y(s)$ and $U(s)$ are the Laplace transforms of the time-domain signals $y(t)$ and $u(t)$ , and $y(0)$ and $\dot{y}(0)$ are the initial conditons for $y(t)$ . Since we assumed that the initial conditions are zero, from the last equation, we obtain:

(3) $\begin{align*}W(s)=\frac{Y(s)}{U(s)}=\frac{1}{s^2+s+1}\end{align*}$

Now, our goal is to compute the step response of the system when $u(t)=h(t)$ , where $h(t)$ is a Heaviside step function. Since $U(s)=1/s$ , the step response in the s-domain has the following form

(4) $\begin{align*}Y(s)=\frac{1}{(s^2+s+1)s}\end{align*}$

So, our goal is to compute the inverse Laplace transform of (4). There are at least two ways to compute this. The first way is to use the formula we explained in the first part of this post. First, we determine the poles. The poles are given by

(5) $\begin{align*}p_{1}=0, \; p_{2}=\frac{-1 +\sqrt{3} i}{2},\; p_{3}=\frac{-1 - \sqrt{3} i}{2}\end{align*}$

So our expression for $Y(s)$ becomes:

(6) $\begin{align*}Y(s)=\frac{K_{1}}{s}+\frac{K_{2}}{s+1-\sqrt{3}i}+\frac{K_{3}}{s+1+\sqrt{3}i}\end{align*}$

We can find the constant $K_{i}$ , $i=1,2,3$ , by applying the previously introduced formula. The difficulty with this approach is that we have to deal with complex numbers and this might be tedious. Instead, there is a more elegant and convinent method to solve this problem. The idea is to represent $Y(s)$ as follows

(7) $\begin{align*}Y(s)=\frac{C_{1}}{s}+\frac{C_{2}s+C_{3}}{s^{2}+s+1}\end{align*}$

By multiplying the expression on the right-hand-side of the last equation, we obtain:

(8) $\begin{align*}Y(s)=\frac{(C_{1}+C_{2})s^2+(C_{1}+C_{3})s+C_{1}}{s(s^2+s+1)}\end{align*}$

By comparing the last equation with (4), we obtain that the constants should satisfy the following system of equations (for more details, see the first part of this post that can be found here):

(9) $\begin{align*}C_{1}=1,\; C_{1}+C_{3} =0,\; C_{1}+C_{2}=0\end{align*}$

By solving this system of equations, we obtain:

(10) $\begin{align*}C_{1}=1,\; C_{2}=-1,\; C_{3}=-1\end{align*}$

So we can write:

(11) $\begin{align*}Y(s)=\underbrace{\frac{1}{s}}_{Y_{1}(s)}-\underbrace{\frac{s+1}{s^2+s+1}}_{Y_{2}(s)}\end{align*}$

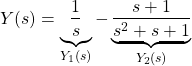
We want to compute the inverse Laplace transform of the last expression. The inverse transform of the first term is easy, it is simply the Heaviside function. On the other hand, the inverse transform of the second term is a bit more complicated. The idea is to write the second term as follows:

(12) $\begin{align*}&Y_{2}(s)=Y_{21}+Y_{22} \\& Y_{21}=\frac{s+\frac{1}{2}}{(s+\frac{1}{2})^{2}+\frac{3}{4}}, \; Y_{22}=\frac{\frac{1}{2}}{(s+\frac{1}{2})^{2}+\frac{3}{4}}\end{align*}$

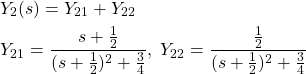
Let us recall some basic properties of the Laplace transform. Let $f(t)$ be a function in the time domain. Them the Laplace transform of the scaled function $f(at)$ is given by:

(13) $\begin{align*}\mathcal{L}\Big[f(at) \Big]= \frac{1}{|a|}F(\frac{s}{a})\end{align*}$

where $F(s)$ is the Laplace transform of $f(t)$ . Let us apply this law to the Laplace transform of $sin(at)$ . We know that

(14) $\begin{align*}\mathcal{L}\Big[sin(t) \Big]=\frac{1}{s^2+1}\end{align*}$

From this expression and from (13) it follows:

(15) $\begin{align*}\mathcal{L}\Big[sin(at) \Big] =\frac{1}{|a|}\cdot\frac{1}{(\frac{s}{a})^2+1}=\frac{a}{s^2+a^2}\end{align*}$

Using the same principle, we can obtain

(16) $\begin{align*}\mathcal{L}\Big[cos(at) \Big]=\frac{s}{s^2+a^2}\end{align*}$

By comparing the expressions (15) and (16) with (12) , we can observe that these expressions are similar except for the fact that instead of $s$ , we have $(s+1/2)$ in (12). In order to complete this example, we need to recall another important property of the Laplace transform. We have:

(17) $\begin{align*}\mathcal{L}\Big[e^{-wt}f(t) \Big]= F(s+w)\end{align*}$

Using (16) and (17), we obtain that the inverse Laplace transform of $Y_{21}$ in (12) is

(18) $\begin{align*}\mathcal{L}^{-1}\Big[Y_{21} \Big]=e^{-\frac{1}{2}t}cos(\frac{\sqrt{3}}{2}t)\end{align*}$

To compute the inverse Laplace transform of $Y_{22}(s)$ , we transform $Y_{22}(s)$ as follows

(19) $\begin{align*}Y_{22}=\frac{1}{2}\cdot \frac{2}{\sqrt{3}}\cdot \frac{\frac{\sqrt{3}}{2}}{(s+\frac{1}{2})^{2}+\frac{3}{4}}=\frac{1}{\sqrt{3}}\frac{\frac{\sqrt{3}}{2}}{(s+\frac{1}{2})^{2}+\frac{3}{4}}\end{align*}$

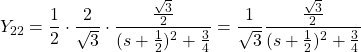
By applying (15) and (17) to (19), we obtain

(20) $\begin{align*}\mathcal{Y}^{-1}\Big[Y_{22}\Big]= \frac{1}{\sqrt{3}} e^{-\frac{1}{2}t}sin(\frac{\sqrt{3}}{2}t)\end{align*}$

Finally, using the previously derived expressions, we obtain:

(21) $\begin{align*}\mathcal{L}^{-1}\Big[Y(s) \Big]= \Big(1 - e^{-\frac{t}{2}}cos(\frac{\sqrt{3}}{2}t)- \frac{1}{\sqrt{3}} e^{-\frac{1}{2}t}sin(\frac{\sqrt{3}}{2}t)\Big) h(t)\end{align*}$

where $h(t)$ is the Heaviside function. The MATLAB code for computing the inverse Laplace transform is given below.

clc
syms s
 
F=1/(s*(s^2+s+1))
 
Factorized=partfrac(F)
 
ilaplace(Factorized)

And the output is:

 
1/(s*(s^2 + s + 1))
 
 
Factorized =
 
1/s - (s + 1)/(s^2 + s + 1)
 
 
ans =
 
1 - exp(-t/2)*(cos((3^(1/2)*t)/2) + (3^(1/2)*sin((3^(1/2)*t)/2))/3)

admin

You might also like

Homework 1 – Strength of Materials – System That Cannot be in Static Equilibrium

Solve a System of Nonlinear Equations in MATLAB

5. Accurately Compute Exponential Moving Averages in Pandas and Python