In this tutorial, we present a simple derivation of the Kalman filter equations. Before reading this tutorial, we advise you to read this tutorial on the recursive least squares method, and this tutorial on mean and covariance matrix propagation through the system dynamics. In the follow-up post which can be found here, we explain how to implement the Kalman filter in Python. The YouTube video accompanying this post is given below.
Model and Model Assumptions
We are considering the following state-space model of a dynamical system:
(1) ![]()
where
 is the discrete-time instant
is the discrete-time instant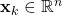 is the state vector at the discrete time instant
is the state vector at the discrete time instant 
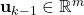 is the control input vector
is the control input vector 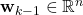 is the disturbance or process noise vector. We assume that
is the disturbance or process noise vector. We assume that 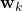 is white, zero mean, uncorrelated, with the covariance matrix given by
is white, zero mean, uncorrelated, with the covariance matrix given by ![Rendered by QuickLaTeX.com Q_{k}=E[\mathbf{w}_{k}\mathbf{w}_{k}^{T}]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-266e7fa5fa9769934ad70b1a27d1a31b_l3.png) , where
, where ![Rendered by QuickLaTeX.com E[\cdot]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-3941b329206b0baa01fad23b819cc5f7_l3.png) is the mathematical expectation operator.
is the mathematical expectation operator. 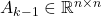 and
and 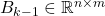 are state and input matrices
are state and input matrices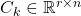 is the output matrix
is the output matrix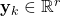 is the output vector (observed measurements)
is the output vector (observed measurements)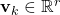 is the measurement noise vector. We assume that
is the measurement noise vector. We assume that 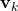 is white, zero mean, uncorrelated, with the covariance matrix given by
is white, zero mean, uncorrelated, with the covariance matrix given by ![Rendered by QuickLaTeX.com R_{k}=E[\mathbf{v}_{k}\mathbf{v}_{k}^{T}]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-90d194c388d2c49758f447864c1e864d_l3.png)
This is a time-varying system. However, if the system is time-invariant, then all the system matrices are constant. We assume that the covariance matrices ![]() ,
, ![]() , as well as system matrices
, as well as system matrices ![]() ,
, ![]() , and
, and ![]() are known. The goal is to design an observer (estimator) that will estimate the state vector
are known. The goal is to design an observer (estimator) that will estimate the state vector ![]() .
.
A priori and a posteriori state estimates, errors, and covariance matrices
In Kalman filtering, we have two important state estimates: a priori state estimates and a posteriori state estimates. Apart from this post and Kalman filtering, a priori and a posteriori are Latin phrases whose meaning is explained here.
The a priori state estimate of the state vector ![]() is obtained implicitly on the basis of the output vector measurements
is obtained implicitly on the basis of the output vector measurements ![]() (as well as on some other information that is not relevant for this discussion). That is, the a priori state estimate is obtained on the basis of the past measurements up to the current discrete-time instant
(as well as on some other information that is not relevant for this discussion). That is, the a priori state estimate is obtained on the basis of the past measurements up to the current discrete-time instant ![]() and NOT on the basis of the measurement
and NOT on the basis of the measurement ![]() at the current discrete-time instant
at the current discrete-time instant ![]() . The a priori state estimate is denoted by
. The a priori state estimate is denoted by
(2) ![]()
where “the hat notation” denotes an estimate, and where the minus superscript denotes the a priori state estimate. The minus superscript originates from the fact that this estimate is obtained before we process the measurement ![]() at the time instant
at the time instant ![]() .
.
The a posteriori estimate of the state ![]() is obtained implicitly on the basis of the measurements
is obtained implicitly on the basis of the measurements ![]() . The a posteriori estimate is denoted by
. The a posteriori estimate is denoted by
(3) ![]()
where the plus superscript in the state estimate notation denotes the fact that the a posteriori estimate is obtained by processing the measurement ![]() obtained at the time instant
obtained at the time instant ![]() .
.
In our previous post, we explained how to derive a recursive least squares method from scratch. We defined and derived the expression for the covariance matrices of estimation errors in the context of recursive least squares filtering. Here, we also need to introduce covariance matrices of the a priori and a posteriori estimation errors. The covariance matrices of the a priori and a posteriori estimation errors are defined as follows
(4) ![Rendered by QuickLaTeX.com \begin{align*}P_{k}^{-}=E[(\mathbf{x}_{k}-\mathbf{x}_{k}^{-})(\mathbf{x}_{k}-\mathbf{x}_{k}^{-})^{T}] \\P_{k}^{+}=E[(\mathbf{x}_{k}-\mathbf{x}_{k}^{+})(\mathbf{x}_{k}-\mathbf{x}_{k}^{+})^{T}]\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-2b8ca14220c48b39e392f9fa5c217e86_l3.png)
where ![]() is the covariance matrix of the a priori estimation error and
is the covariance matrix of the a priori estimation error and ![]() is the covariance matrix of the a posteriori estimation error.
is the covariance matrix of the a posteriori estimation error.
Derivation of Kalman Equations from the Recursive-Least Squares Method
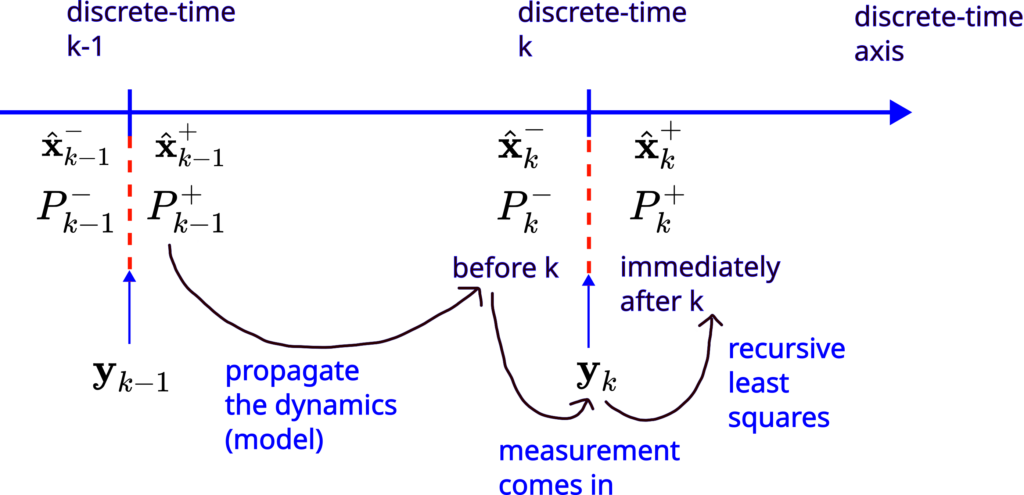
The following figure illustrates how the Kalman filter works in practice.
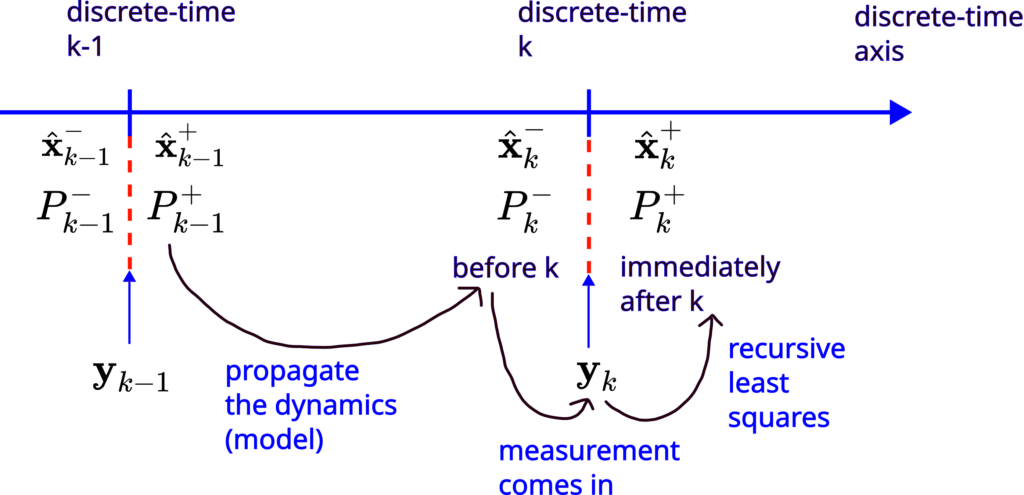
For the time being it is beneficial to briefly explain this figure. Even if some concepts are not completely clear, they will become clear by the end of this post. Immediately after the discrete-time instant ![]() , we compute the a posteriori state estimate
, we compute the a posteriori state estimate ![]() and the covariance matrix of the estimation error
and the covariance matrix of the estimation error ![]() . Then, we propagate these quantities through the equations describing the system dynamics and covariance matrix propagation (that is also derived on the basis of the system dynamics). That is, we propagate the a posteriori state and covariance through our model. By propagating these quantities, we obtain the a priori state estimate
. Then, we propagate these quantities through the equations describing the system dynamics and covariance matrix propagation (that is also derived on the basis of the system dynamics). That is, we propagate the a posteriori state and covariance through our model. By propagating these quantities, we obtain the a priori state estimate ![]() and the covariance matrix of the estimation error
and the covariance matrix of the estimation error ![]() for the time step
for the time step ![]() . Then, after the measurement vector
. Then, after the measurement vector ![]() is observed at the discrete-time step
is observed at the discrete-time step ![]() , we use this measurement and the recursive-least squares method to compute the a posteriori estimate
, we use this measurement and the recursive-least squares method to compute the a posteriori estimate ![]() and the covariance matrix of the estimation error
and the covariance matrix of the estimation error ![]() for the time instant
for the time instant ![]() .
.
Now that we have a general idea of how Kalman filtering works, let us now derive the Kalman filter equations. At the initial time instant ![]() , we need to choose an initial guess of the state estimate. Let this chosen initial guess of the state estimate be denoted by
, we need to choose an initial guess of the state estimate. Let this chosen initial guess of the state estimate be denoted by ![]() . This will be our initial a posteriori state estimate, that is
. This will be our initial a posteriori state estimate, that is
(5) ![]()
Then, the question is how to compute the a priori estimate ![]() for the time instant
for the time instant ![]() , before the measurements are taken?
, before the measurements are taken?
The natural answer is that the system states, as well as the estimates, need to satisfy the system dynamics (1), and consequently,
(6) ![]()
where we excluded the disturbance part since the disturbance vector is not known. Besides the initial guess of the estimate, we also need to select an initial guess of the covariance matrix of the estimation error. That is, we need to select ![]() . If we have perfect knowledge about the initial state, then we select
. If we have perfect knowledge about the initial state, then we select ![]() as a zero matrix, that is
as a zero matrix, that is ![]() , where
, where ![]() is an identity matrix. This is because the covariance matrix of the estimation error is the measure of uncertainty, and if we have perfect knowledge, then the measure of uncertainty should be zero. On the other hand, if we do not have any a priori knowledge of the initial state, then
is an identity matrix. This is because the covariance matrix of the estimation error is the measure of uncertainty, and if we have perfect knowledge, then the measure of uncertainty should be zero. On the other hand, if we do not have any a priori knowledge of the initial state, then ![]() , where
, where ![]() is a large number. Next, we need to compute the covariance matrix of the a priori state estimation error, that is, we need to compute
is a large number. Next, we need to compute the covariance matrix of the a priori state estimation error, that is, we need to compute ![]() . In our previous post, which can be found here, we derived the expression for the time propagation of the covariance matrix of the state estimation error:
. In our previous post, which can be found here, we derived the expression for the time propagation of the covariance matrix of the state estimation error:
(7) ![]()
By using this expression, we obtain the following equation for ![]()
(8) ![]()
So this is the best we can do at the initial time step ![]() before we obtain measurement information. We computed the a priori estimate
before we obtain measurement information. We computed the a priori estimate ![]() and the covariance matrix
and the covariance matrix ![]() for the time step
for the time step ![]() , and before the measurement
, and before the measurement ![]() at the time step
at the time step ![]() has arrived.
has arrived.
At the time instant ![]() , the measurement
, the measurement ![]() , arrives. Then, the natural question is how to update the a priori estimate
, arrives. Then, the natural question is how to update the a priori estimate ![]() and the covariance matrix
and the covariance matrix ![]() ?
?
To update these quantities, we need to use the recursive least-squares method. We derived the equations of the recursive least-squares method in our previous post, which can be found here. Here are the recursive least-squares equations:
- Update the gain matrix
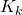 :
:(9)
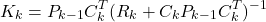
- Update the estimate:
(10)
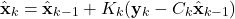
- Propagate the covariance matrix by using this equation:
(11)
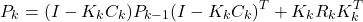
or this equation(12)
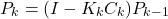
Now, the question is how to use these equations to derive the Kalman filter equations? First, we perform the following substitutions in the recursive least-squares equations (these substitutions will be explained later in the text):
(13) ![]()
(14) ![]()
(15) ![]()
(16) ![]()
Here is the main idea behind these substitutions. Let us first focus on the equation (13). In the case of the recursive least squares method, the covariance before the measurement arrives is ![]() . In the case of the Kalman filter,
. In the case of the Kalman filter, ![]() becomes
becomes ![]() , since
, since ![]() is the covariance before the measurement arrived. Next, let us focus on (14). In the case of the recursive least squares method, the covariance after the measurement arrives is
is the covariance before the measurement arrived. Next, let us focus on (14). In the case of the recursive least squares method, the covariance after the measurement arrives is ![]() . In the case of the Kalman filter,
. In the case of the Kalman filter, ![]() becomes
becomes ![]() , since
, since ![]() is the updated covariance after the measurement arrived. Next, let us focus on (15). In the case of the recursive least squares,
is the updated covariance after the measurement arrived. Next, let us focus on (15). In the case of the recursive least squares, ![]() is the state estimate before the measurement
is the state estimate before the measurement ![]() arrived. Consequently, in the case of the Kalman filter,
arrived. Consequently, in the case of the Kalman filter, ![]() becomes the a priori estimate
becomes the a priori estimate ![]() , since
, since ![]() does not take into account the measurement
does not take into account the measurement ![]() . Finally, let us focus on (16). In the case of the recursive least squares method,
. Finally, let us focus on (16). In the case of the recursive least squares method, ![]() is the state estimate that takes into account the measurement
is the state estimate that takes into account the measurement ![]() . Consequently, in the case of the Kalman filter,
. Consequently, in the case of the Kalman filter, ![]() becomes
becomes ![]() , since
, since ![]() takes into account the measurement
takes into account the measurement ![]() obtained at the time instant
obtained at the time instant ![]() .
.
After these substitutions, we obtain the update equations:
(17) ![]()
(18) ![]()
(19) ![]()
Now, let us go back at the time instant ![]() . By using the newly established update equations, we update
. By using the newly established update equations, we update ![]() and
and ![]() , as follows
, as follows
(20) 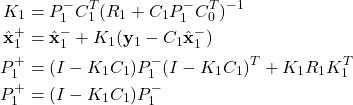
As the result, we obtained ![]() and the a posteriori estimate
and the a posteriori estimate ![]() . Next, similarly to the initial step, we propagate
. Next, similarly to the initial step, we propagate ![]() through the system dynamics (model of the system), and
through the system dynamics (model of the system), and ![]() through covariance propagation equation:
through covariance propagation equation:
(21) 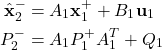
to obtain ![]() and
and ![]() . After this step, we compute the a posteriori estimate and the covariance matrix of the estimation error by using Eqs. (17), (18), and (19) for
. After this step, we compute the a posteriori estimate and the covariance matrix of the estimation error by using Eqs. (17), (18), and (19) for ![]() . We learned that the two main steps of the Kalman filter are:
. We learned that the two main steps of the Kalman filter are:
- Before the measurement arrives, use the system dynamics to propagate the a posteriori estimate and covariance matrix of the estimation error from the step
 , to obtain the a priori estimate and covariance matrix of the estimation error for the step
, to obtain the a priori estimate and covariance matrix of the estimation error for the step  .
. - At the time step
 , use the recursive least squares equations, and the obtained measurement, to compute the a posteriori estimate and the covariance matrix of the estimation error.
, use the recursive least squares equations, and the obtained measurement, to compute the a posteriori estimate and the covariance matrix of the estimation error.
This is illustrated in Fig. 2 (the same as Fig. 1 which is repeated here for completeness).
Let us now summarize the Kalman filter equations.
Summary of the derived Kalman filter equations
In the initial step, we select and initial estimate ![]() and the covariance matrix of the estimation error
and the covariance matrix of the estimation error ![]() . Then, for
. Then, for ![]() , we perform steps 1 and 2 summarized below
, we perform steps 1 and 2 summarized below
Step 1: Propagate the a posteriori estimate ![]() and the covariance matrix of the estimation error
and the covariance matrix of the estimation error ![]() , through the system dynamics to obtain the a priori state estimate and the covariance matrix of the estimation error for the step
, through the system dynamics to obtain the a priori state estimate and the covariance matrix of the estimation error for the step ![]() :
:
(22) 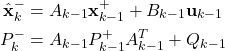
Step 2: Obtain the measurement ![]() . Use this measurement, and the a priori estimate
. Use this measurement, and the a priori estimate ![]() and the covariance matrix of the estimation error
and the covariance matrix of the estimation error ![]() to compute the a posteriori state estimate and the covariance matrix of the estimation error
to compute the a posteriori state estimate and the covariance matrix of the estimation error
(23) 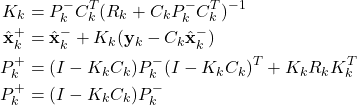
Here are a few comments about the derived Kalman filter equations. The matrix ![]() is called the Kalman filter gain matrix. Then, the equation for the covariance update
is called the Kalman filter gain matrix. Then, the equation for the covariance update
(24) ![]()
is more numerically stable and robust than the alternative equation
(25) ![]()
Consequently, the equation (24) is preferable for computing the covariance update. Another important thing to mention is that the Kalman filter gain ![]() does not depend on the measurements
does not depend on the measurements ![]() . This is because the calculations of
. This is because the calculations of ![]() ,
, ![]() , and
, and ![]() only depend on the system matrices
only depend on the system matrices ![]() ,
, ![]() , and
, and ![]() and
and ![]() . This means that the Kalman filter matrices
. This means that the Kalman filter matrices ![]() , for
, for ![]() can be precomputed before the Kalman filter starts to operate online. This is important for saving computational time in embedded systems.
can be precomputed before the Kalman filter starts to operate online. This is important for saving computational time in embedded systems.