In our previous post, given here, we have explained how to define homogenous transforms to describe the rotation and translation of one coordinate system with respect to another. Homogeneous transform is actually a matrix that describes the translation and rotation of one coordinate system with respect to another one. In this post, we explain how to use homogeneous transform to solve a forward kinematics problem.
Consider a robotic manipulator with two degrees of freedom shown in the figure below
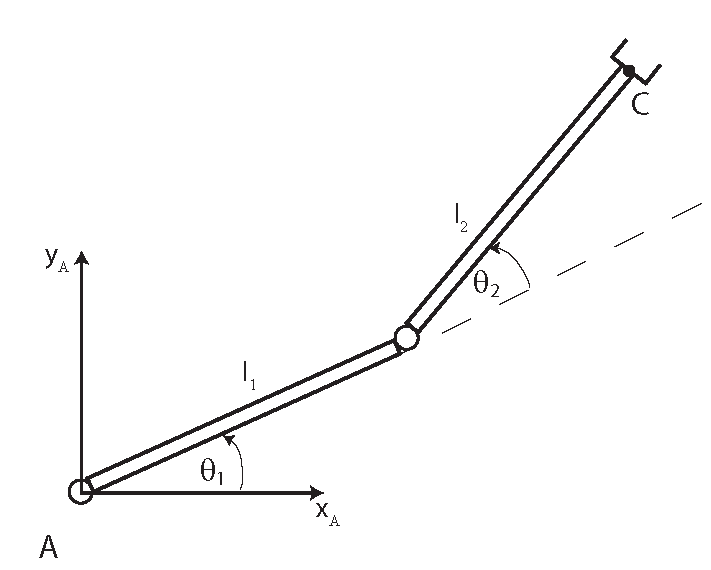
The forward kinematics problem can be postulated as follows:
Consider the robotic manipulator shown in Fig. 1. Given the joint coordinates ![]() and
and ![]() , and the link lengths
, and the link lengths ![]() and
and ![]() , compute the coordinates of the point
, compute the coordinates of the point ![]() (end-effector point) in the world coordinate system A.
(end-effector point) in the world coordinate system A.
Solution 1 (without using homogeneous transform):
We have:
(1) ![]()
where ![]() and
and ![]() are the x and y coordinates of the point
are the x and y coordinates of the point ![]() in the world coordinate system
in the world coordinate system ![]() . Now, let us recall basic trigonometric formulas:
. Now, let us recall basic trigonometric formulas:
(2) ![]()
By substituting these formulas in (3), we obtain
(3) 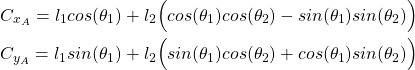
Solution 2 (by using homogeneous transform):
First, we assign coordinate systems. We assign a coordinate system to every axis (joint). The coordinate systems are shown in the figure below
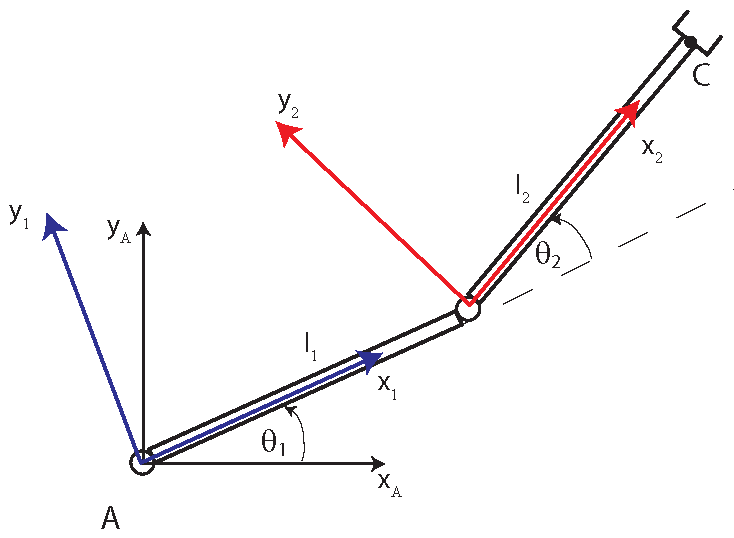
The point ![]() in the coordinate system
in the coordinate system ![]() has the following coordinates
has the following coordinates
(4) ![]()
As we have explained in our previous post, the notation ![]() means that the coordinates of the vector
means that the coordinates of the vector ![]() are represented in the coordinate system
are represented in the coordinate system ![]() . On the other hand, we can assign homogeneous transformation, to represent the vector
. On the other hand, we can assign homogeneous transformation, to represent the vector ![]() in the coordinate system
in the coordinate system ![]() :
:
(5) ![]()
where ![]() is the representation of the vector
is the representation of the vector ![]() in the coordinate system
in the coordinate system ![]()
(6) ![]()
and the rotation matrix ![]() is given by
is given by
(7) ![]()
The notation ![]() means that the rotation matrix represents transformation from the coordinate system
means that the rotation matrix represents transformation from the coordinate system ![]() to coordinate system
to coordinate system ![]() (lower index means “from”, and the upper index means “to”). On the other hand, the representation of the vector
(lower index means “from”, and the upper index means “to”). On the other hand, the representation of the vector ![]() in the coordinate system
in the coordinate system ![]() is given by another homogeneous transformation
is given by another homogeneous transformation
(8) ![]()
where
(9) ![]()
and the vector ![]() is 2 times 1 vector of zeros, since the coordinate systems
is 2 times 1 vector of zeros, since the coordinate systems ![]() and
and ![]() are located at the same point, and consequently, there is no translation of coordinate systems. By combining (5) and (8), we obtain
are located at the same point, and consequently, there is no translation of coordinate systems. By combining (5) and (8), we obtain
(10) 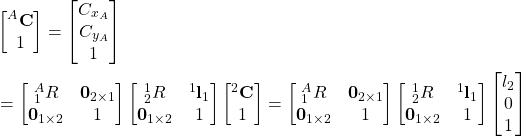
That is
(11) 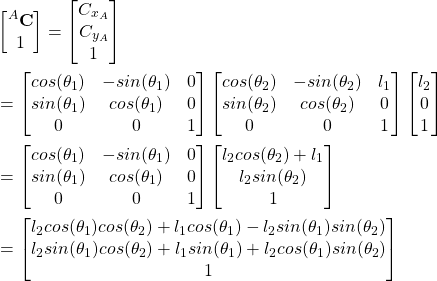
This result is identical to (3).