Example of Designing a Phase Lead Controller (Compensator) in MATLAB – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In our previous post, which can be found here, we derived the main equations of the phase lead controller. Furthermore, in the same post, we summarized a procedure for designing the phase lead controller. In this post, we explain how this procedure can be used to design the parameters of the phase lead controller. The YouTube tutorial accompanying this tutorial is given below.

Problem

Consider the following open-loop system:

(1) $\begin{align*}W(s)=\frac{10}{s(s+1)}\end{align*}$

Design the lead compensator such that the phase margin of the compensated system is at least 50 degrees.

Summary of the Design Procedure for the Phase Lead Compensator

Design specification and goal: Achieve the Phase Margin (PM) of the compensated system that is larger or equal to the minimum desired value of the PM. Design the parameters $a$ and $T$ of the lead compensator

(2) $\begin{align*}G_{c}(s)=\frac{1+aTs}{1+Ts},\;\; a>1\end{align*}$

The Bode plot of the phase lead compensator is shown in the figure below.

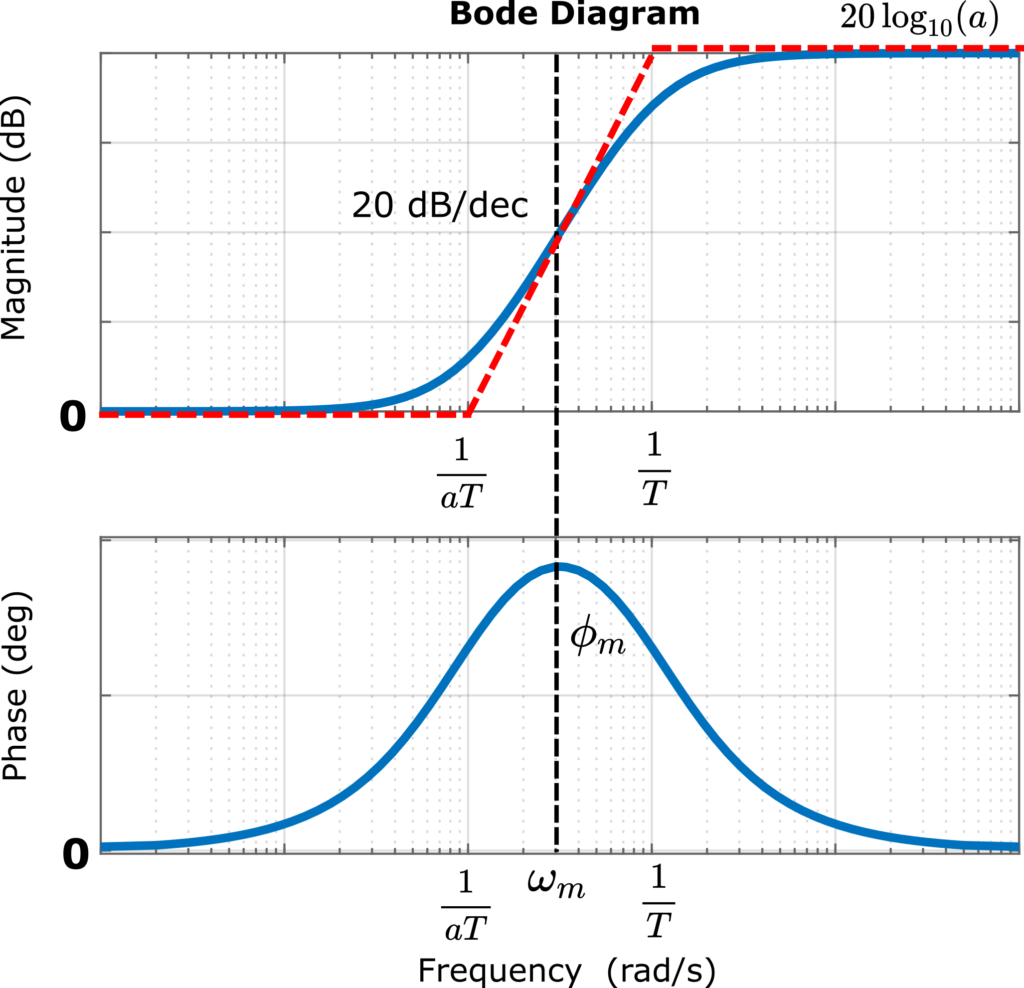
Fig 1: Bode plot of the phase lead compensator (2).

PROCEDURE 1:

Step 1: Plot the Bode plot of the uncompensated system. Read the PM of the uncompensated system. On the basis of the PM of the uncompensated system and on the basis of the minimum desired PM, calculate the necessary value of $\phi_{m}$ (maximum phase of the lead compensator), as the difference between the minimum desired PM and the PM of the uncompensated system. That is, $\phi_{m}$ is the value of phase that needs to be added to the PM of the uncompensated system. Optionally, add a few degrees to this difference.

Step 2: For calculated $\phi_{m}$ , determine the parameter $a$ of the compensator by using the following formula

(3) $\begin{align*}a=\frac{1+\sin(\phi_m)}{1-\sin(\phi_m)}\end{align*}$

Step 3: Select $\omega_{m}$ (frequency of the phase lead compensator that produces the maximum phase $\phi_{m}$ of the compensator) as the frequency where the gain of the uncompensated system is equal to $-10\log_{10}(a)$ . This will ensure that the gain cross-over frequency of the compensated system is approximately at $\omega_{m}$ .

Step 4: Select the parameter $T$ as

(4) $\begin{align*}T=\frac{1}{\omega_{m}\sqrt{a}}\end{align*}$

Step 5: Plot the Bode plot, and check if the design specifications are met. If they are met, then we have designed the filter parameters $a$ and $T$ . If not, increase the previously computed value of $\phi_{m}$ , and repeat the steps 2, 3, 4, and 5.

Solution

Here, we present the solution of the problem. The MATLAB codes are given after each graph.

STEP 1: The bode plot of the open-loop system is given below.

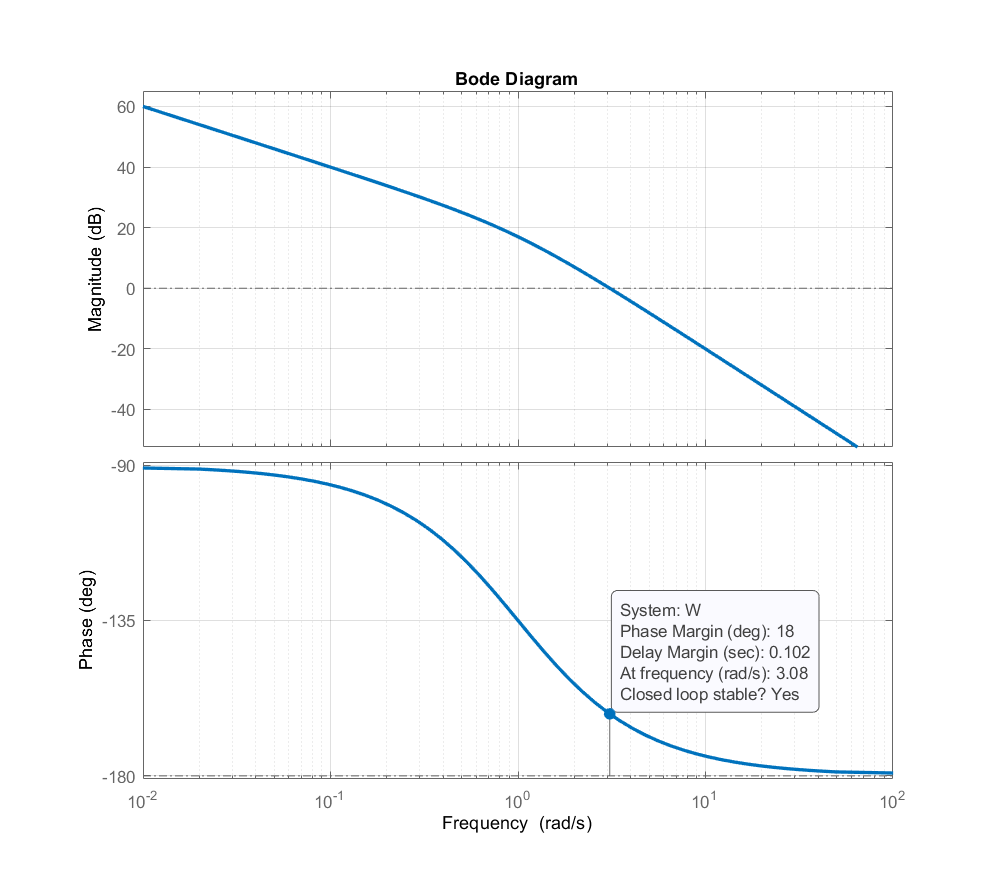
Fig 2: Bode plot of the open-loop uncompensated system (1)

We can observe that the phase margin of the open-loop uncompensated system is $18$ degrees at the gain cross-over frequency of $3.08$ rad/s. Consequently, since the desired phase margin of the compensated system is 50 degrees, we have that the maximal phase of the lead compensator is

(5) $\begin{align*}\phi_{m}=50-18=32\end{align*}$

Here, it is also instructive to plot the step response of the closed-loop system without the compensator. The step response of the closed-loop system is given below.

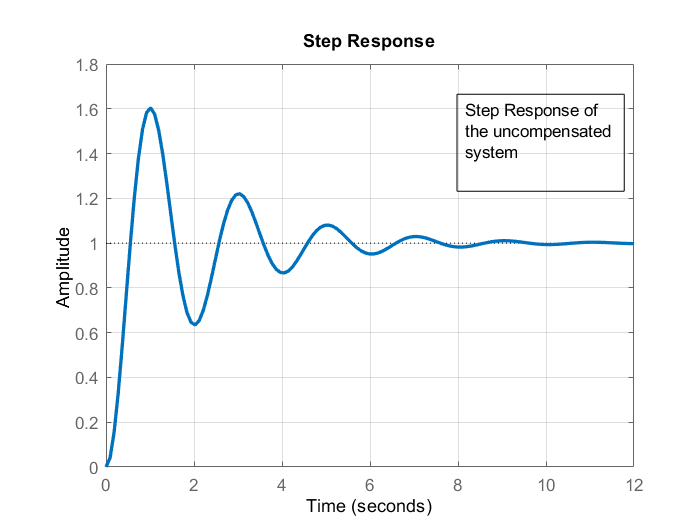
Fig 3: Step response of the closed-loop uncompensated system.

From Fig. 3., we can observe that the main issue with the step response of the closed loop of the uncompensated system is the large damping ratio. By increasing the phase margin, we will decrease the damping without affecting the steady-state characteristics.

We used the following MATLAB code lines to generate these plots

W=tf(10,[1 1 0])
figure(1)
bode(W)
Wfeedback=feedback(W,1)
figure(2)
step(Wfeedback)

STEP 2: We use the following formula to determine the parameter $a$

(6) $\begin{align*}a=\frac{1+\sin(\phi_m)}{1-\sin(\phi_m)}\end{align*}$

Before we can implement this formula in MATLAB, we need to convert the degrees to radians. We have

(7) $\begin{align*}\phi_{m}=32\cdot \frac{\pi}{180}=0.5585 \text{radians}\end{align*}$

By substituting this value in (6), by using MATLAB, we obtain

(8) $\begin{align*}a=3.2546\end{align*}$

We used the following MATLAB code to compute $a$

phiM=50-18
phiMr=phiM*pi/180
a= (1+sin(phiMr))/(1-sin(phiMr))

STEP 3: We have that

(9) $\begin{align*}-10\log_{10}(a)=-5.1250\end{align*}$

By searching for the frequency that produces this magnitude (gain) from Fig. 2, we obtain $\omega_{m}\approx 4.15$ .

STEP 4: The parameter $T$ is then determined by

(10) $\begin{align*}T=\frac{1}{\omega_{m}\sqrt{a}}=\frac{1}{4.15\cdot \sqrt{3.2546}}=0.1336\end{align*}$

The MATLAB code is given below

wc=4.15;
T=1/(sqrt(a)*wc)

STEP 5: The Bode plot of the compensated system in the first iteration is given below

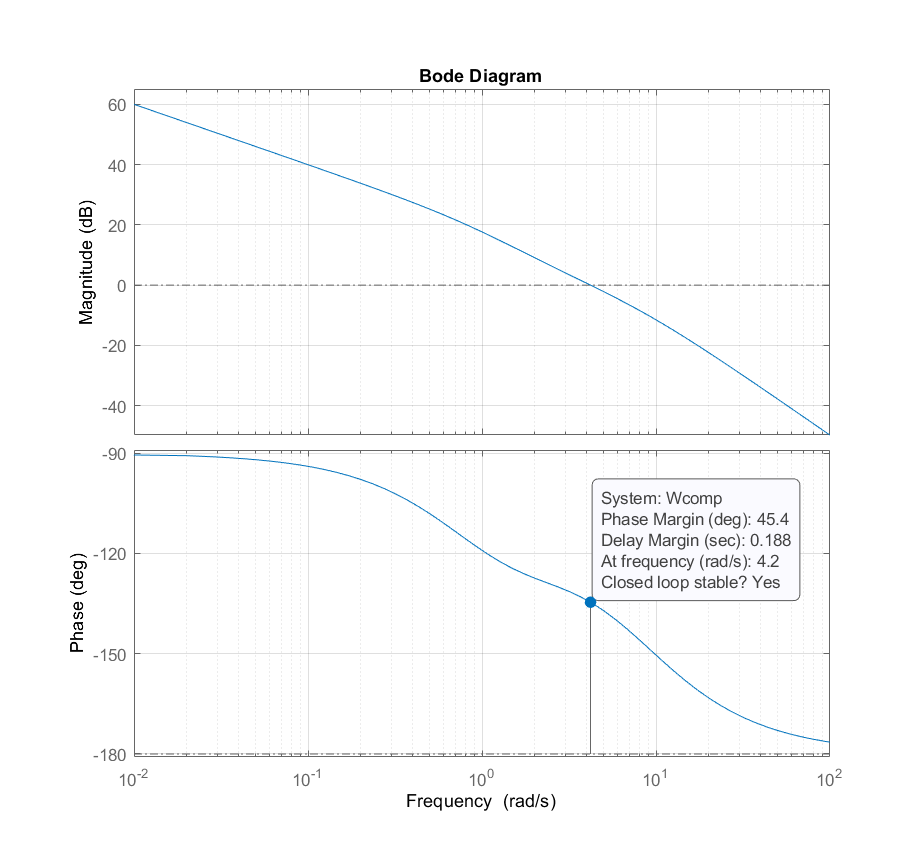
Fig 4: Bode plot of the compensated system in the first iteration.

We can see that the phase margin improved. However, it is still 5 degrees less than the desired value of 50 degrees. Consequently, we need to repeat the steps 2,3,4, and 5, by increasing the value of $\phi_{m}$ .

This graph is generated by the following MATLAB code:

Gc=tf([a*T 1],[T 1])
Wcomp=Gc*W

figure(3)
bode(Wcomp)

REPETITION OF STEPS 2,3,4, and 5:

Here, we increase the value of $\phi_m$ to 40. We obtained the following parameters:

(11) $\begin{align*}a=4.5989,\; \omega_{c}=4.5,\;\; T=0.1036\end{align*}$

The compensator is given by

(12) $\begin{align*}G_{c}(s)=\frac{0.4766 s + 1}{0.1036 s + 1}\end{align*}$

The compensated system for this value is shown below.

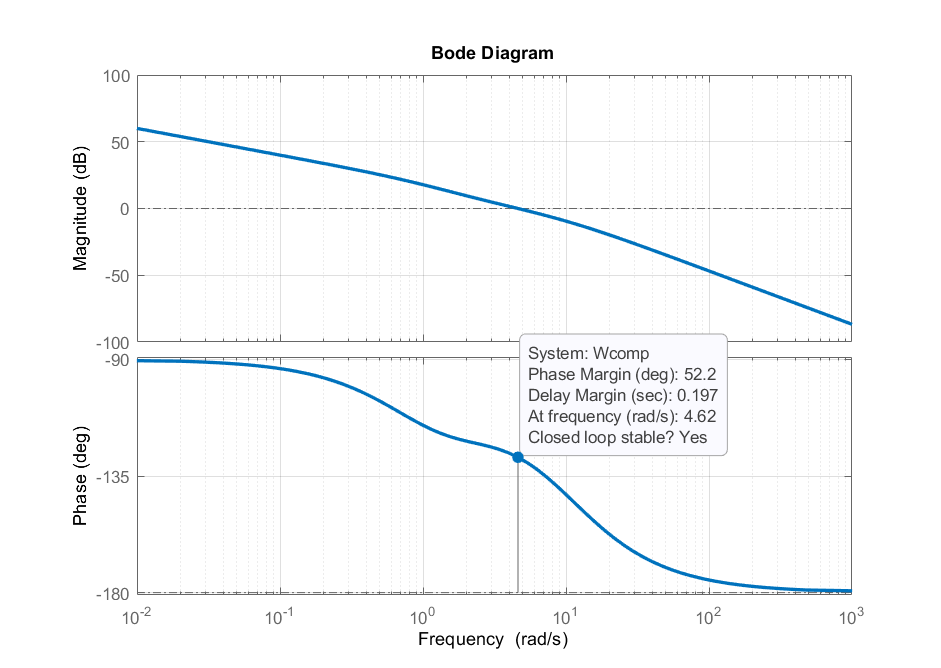
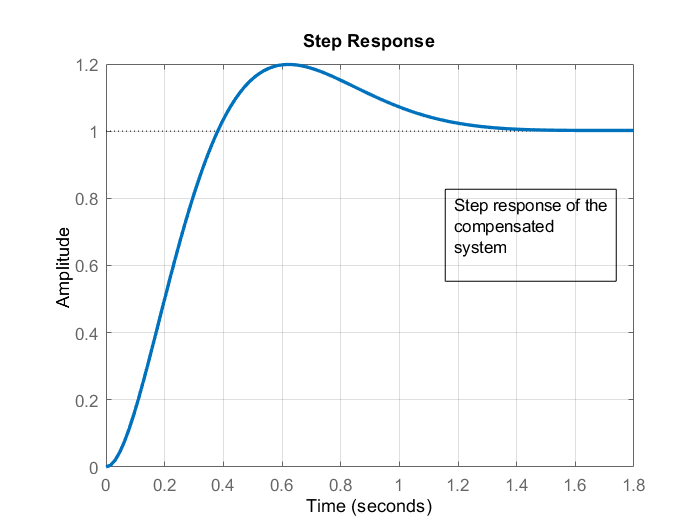
Figure 5: Bode plot of the final compensated open-loop system.

The step response of the compensated system is given below. We can observe that the damping is significantly reduced as well as the settling time.

Problem

Summary of the Design Procedure for the Phase Lead Compensator

Solution

admin

You might also like

Create Movies from Images or Matrices in MATLAB

Homework Assignment 3

Introduction to Eigen C++ Matrix Library