In this control engineering and control theory tutorial, we provide a correct and detailed explanation of state observers that are used for state estimation of linear dynamical systems in the state-space form. We also explain how to implement and simulate observers in Python. The main motivation for creating this video tutorial comes from the fact that in a number of control engineering books and online tutorials, observers are presented from the mathematical perspective without providing enough practical insights and intuitive explanations of observers and state estimators. In contrast, in this control engineering tutorial, we provide an intuitive explanation of observers as well as a concise mathematical explanation. The observer developed in this tutorial belongs to the class of Luenberger observers. We use the pole placement method to design the observer gain matrix. We also explain the concept of duality between the observer design and feedback control problems. Finally, we design, implement, and simulate the observer in Python by using the Control Systems Library and the function place(). The complete Python code files developed in this tutorial are given here.
The YouTube tutorial accompanying this lecture is given below.
Motivational Example
As a motivational example, we consider a system shown in the figure below.
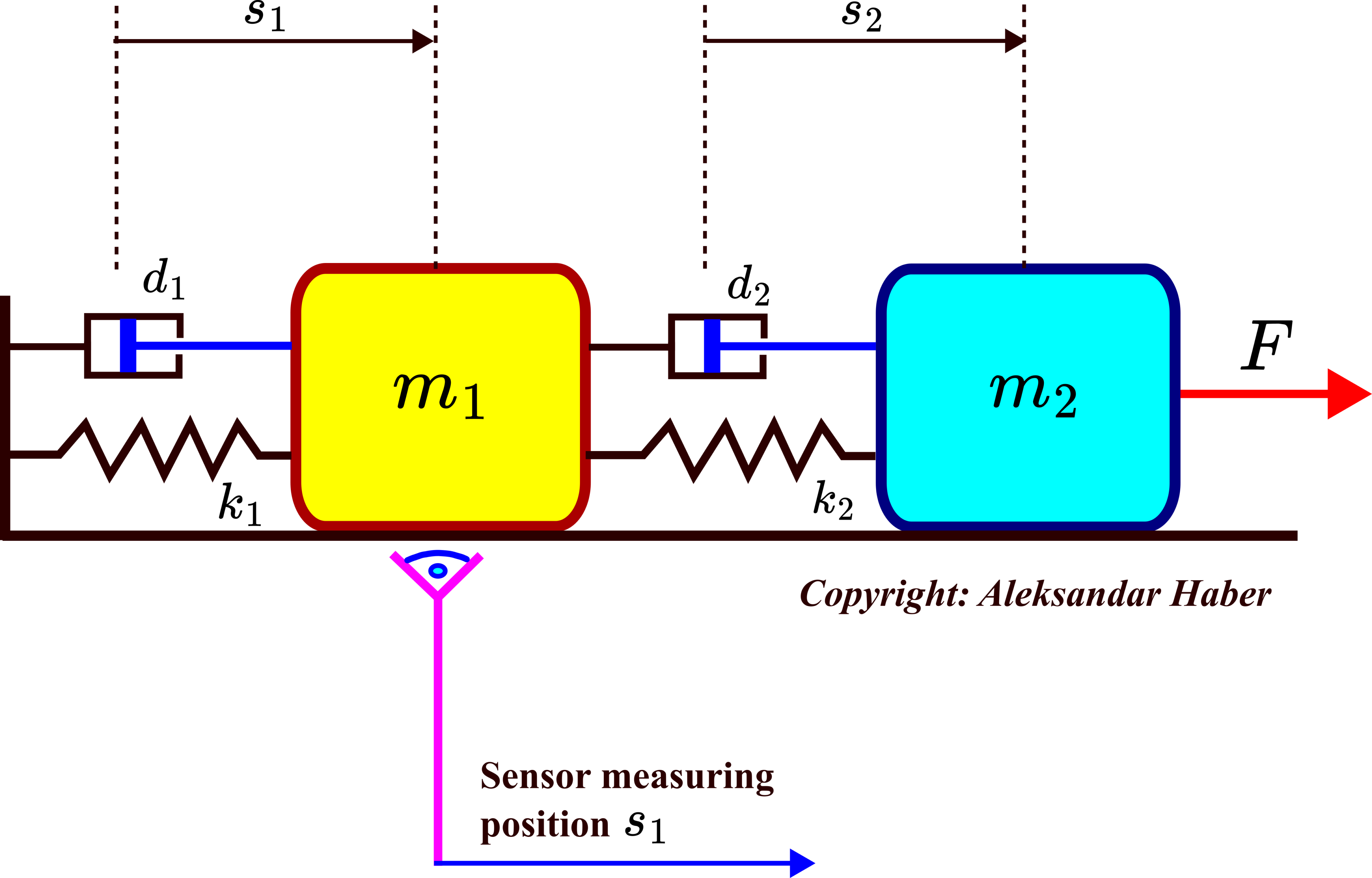
This system consists of two objects with masses ![]() and
and ![]() that are connected by springs and dampers. We assume that spring constants
that are connected by springs and dampers. We assume that spring constants ![]() and
and ![]() are given, as well as damping constants
are given, as well as damping constants ![]() and
and ![]() . The force
. The force ![]() is acting on the second object and since the second object is connected to the first object, it moves both objects. The position of the first object with respect to its equilibrium point is denoted by
is acting on the second object and since the second object is connected to the first object, it moves both objects. The position of the first object with respect to its equilibrium point is denoted by ![]() , and the position of the second object with respect to its equilibrium point is denoted by
, and the position of the second object with respect to its equilibrium point is denoted by ![]() . We assume that the position
. We assume that the position ![]() is observed by a distance sensor. Let
is observed by a distance sensor. Let ![]() and
and ![]() denote the velocities of the first and second objects, respectively. By introducing the state-space variables
denote the velocities of the first and second objects, respectively. By introducing the state-space variables
(1) ![]()
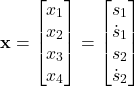
The complete state vector of the system is given by
(2) 
We want to provide the answer to the following question and solve the state estimation problem formulated below:
- Can we uniquely estimate the complete state vector by observing the time sequence of the position
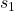 (state variable
(state variable 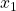 )?
)? - If yes, design a state estimator (observer) that will continuously reconstruct or estimate the complete state vector
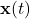 given by (2), from the observed time sequence of the position
given by (2), from the observed time sequence of the position 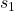 .
.
To solve both of these two problems, we need to know the model of the system. In our previous tutorial given here, we derived a state-space model of the system and we explained how to simulate the state-space model in Python. The state space model has the following form
(3) ![]()
where
(4) 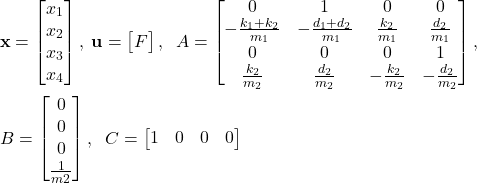
The answer to question 1 is related to the problem of observability of the state-space model (3). In our tutorial given here, we thoroughly explained the observability problem and the concept of observability of dynamical systems. Briefly speaking, if the system with its state-space model (3) is observable, then we can uniquely estimate the state vector ![]() from the sequence or time series of the output measurements.
from the sequence or time series of the output measurements.
Here, for presentation clarity, it is important to state the observability condition for linear systems in the most general form
(5) ![]()
where ![]() ,
, ![]() , and
, and ![]() are the system matrices,
are the system matrices, ![]() is the n-dimensional state vector,
is the n-dimensional state vector, ![]() is the m-dimensional input vector, and
is the m-dimensional input vector, and ![]() is r-dimensional output vector. The observability matrix has the following form
is r-dimensional output vector. The observability matrix has the following form
(6) 
where it should be kept in mind that ![]() is the state order of the system. Here, it is important to emphasize that in our previous tutorial given here, we derived the observability condition for the discrete-time systems. However, in this tutorial, we consider continuous-time systems. It turns out that the observability rank condition is the same for both discrete-time and continuous-time systems. That is, it boils down to the problem of testing the rank of the observability matrix given by (7). The system (5) is observable if and only if the rank of the observability matrix is equal to the state order
is the state order of the system. Here, it is important to emphasize that in our previous tutorial given here, we derived the observability condition for the discrete-time systems. However, in this tutorial, we consider continuous-time systems. It turns out that the observability rank condition is the same for both discrete-time and continuous-time systems. That is, it boils down to the problem of testing the rank of the observability matrix given by (7). The system (5) is observable if and only if the rank of the observability matrix is equal to the state order ![]() .
.
Let us now go back to the double mass-spring-damper system from the beginning of this tutorial. Since, ![]() (we have
(we have ![]() state variables), to test observability, we construct the observability matrix
state variables), to test observability, we construct the observability matrix
(7) 
and we check the numerical rank of this matrix. The system is observable if and only if the rank of the observability matrix is equal to the state order. In our case, the state order is ![]() (we have four state variables), and consequently, the rank of the observability matrix (7) should be equal to
(we have four state variables), and consequently, the rank of the observability matrix (7) should be equal to ![]() . One of the approaches for checking the numerical rank of this matrix is to compute the Singular Value Decomposition (SVD) of this matrix and to check the magnitude of the smallest singular value. If the smallest singular value is not close to zero, then we can conclude that the system is numerically observable. In MATLAB or Python, we can also use the rank function to compute matrix rank. However, the rank function will only provide us with a YES or NO answer, without providing us with more insights into the degree of observability. That is, how far is our matrix from losing the full rank, and consequently, how far is our system from an unobservable system? For example, if the computed singular value of the observability matrix is
. One of the approaches for checking the numerical rank of this matrix is to compute the Singular Value Decomposition (SVD) of this matrix and to check the magnitude of the smallest singular value. If the smallest singular value is not close to zero, then we can conclude that the system is numerically observable. In MATLAB or Python, we can also use the rank function to compute matrix rank. However, the rank function will only provide us with a YES or NO answer, without providing us with more insights into the degree of observability. That is, how far is our matrix from losing the full rank, and consequently, how far is our system from an unobservable system? For example, if the computed singular value of the observability matrix is ![]() or a smaller number, then we can conclude that from the practical point of view, the system is poorly observable or practically unobservable. We will explain how to test the observability condition in Python later on in this tutorial. For the time being, it is important to know that indeed, the system is observable by only measuring the position
or a smaller number, then we can conclude that from the practical point of view, the system is poorly observable or practically unobservable. We will explain how to test the observability condition in Python later on in this tutorial. For the time being, it is important to know that indeed, the system is observable by only measuring the position ![]() .
.
Now, we need to address the second problem, that is, we need to design an estimator that will continuously estimate the state vector from the sequence of the measurements of ![]() . This is the main topic of this tutorial that is thoroughly explained in this tutorial.
. This is the main topic of this tutorial that is thoroughly explained in this tutorial.
Observers for State Estimation of Dynamical Systems
In this section, we address the second problem stated in the previous section:
Design a state estimator (observer) that will continuously estimate the complete state vector ![]() from the time sequence of the output measurements
from the time sequence of the output measurements ![]() .
.
Here, for clarity, we repeat the state-space model
(8) ![]()
With the state-space model (8), we associate a state observer that has the following form
(9) ![]()
OVER HERE IT IS VERY IMPORTANT TO EMPHASIZE THAT THE OBSERVER (9) IS ACTUALLY AN ALGORITHM THAT CAN BE IMPLEMENTED IN CONTROL HARDWARE. OVER HERE, THIS ALGORITHM IS REPRESENTED AS A CONTINUOUS TIME-STATE EQUATION (DIFFERENTIAL EQUATION). IN PRACTICE, IT IS OFTEN DISCRETIZED AND IMPLEMENTED AS A DISCRETE-TIME FILTER IN CONTROL HARDWARE.
Here is the explanation of the observer vectors and matrices:
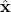 is the state of the observer. The goal of the observer is to approximate and track the state of the system
is the state of the observer. The goal of the observer is to approximate and track the state of the system  over time. That is,
over time. That is, 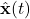 should accurately approximate and track the state of the system
should accurately approximate and track the state of the system 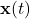 , starting from some initial guess of the state, denoted by
, starting from some initial guess of the state, denoted by 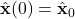 . Here, it should also be kept in mind that the “hat” notation above the state of the observer is deliberately introduced in order to distinguish the state of the system from the state of the observer since these are two different quantities.
. Here, it should also be kept in mind that the “hat” notation above the state of the observer is deliberately introduced in order to distinguish the state of the system from the state of the observer since these are two different quantities.- The matrix
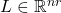 (
( is the output dimension and
is the output dimension and 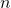 is the state dimension) is the observer gain matrix that should be designed by the user (more about this in the sequel).
is the state dimension) is the observer gain matrix that should be designed by the user (more about this in the sequel). - The term
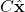 is the prediction of the system’s output made by the observer. This is because the state of the observer is propagated through the output matrix.
is the prediction of the system’s output made by the observer. This is because the state of the observer is propagated through the output matrix. - The term
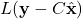 is the observer correction term. This term is called the correction term because of the following. If the observer state
is the observer correction term. This term is called the correction term because of the following. If the observer state 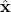 is equal to the system state
is equal to the system state  , then the correction term is zero. This is because the observer uses the output matrix
, then the correction term is zero. This is because the observer uses the output matrix 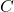 of the system, and consequently the output prediction made by the observer is equal to the output of the system
of the system, and consequently the output prediction made by the observer is equal to the output of the system 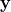 . Consequently, since the observer correction term is zero, the state of the observer is propagated through the observer dynamics (9) in the same manner as the true state of the system (8). In this case, the observer will perfectly track the state of the system. However, if the term
. Consequently, since the observer correction term is zero, the state of the observer is propagated through the observer dynamics (9) in the same manner as the true state of the system (8). In this case, the observer will perfectly track the state of the system. However, if the term 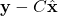 is different from zero, the observer correction term will be different from zero, and the observer state dynamics (9) will be influenced by the correction term that serves as an additional input. The goal of this input is to try to correct the state of the observer in the next time instant
is different from zero, the observer correction term will be different from zero, and the observer state dynamics (9) will be influenced by the correction term that serves as an additional input. The goal of this input is to try to correct the state of the observer in the next time instant 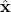 such that it becomes closer to the actual state of the system
such that it becomes closer to the actual state of the system  .
.
The observer diagram is shown below.

The observer inputs are the system control input ![]() , and the output of the system
, and the output of the system ![]() . The output of the observer is the state estimate
. The output of the observer is the state estimate ![]() .
.
Here, again, we will repeat the main goal of the observer.
The goal of the observer is to approximate and track the state of the system ![]() over time. That is,
over time. That is, ![]() should accurately approximate and track the state of the system
should accurately approximate and track the state of the system ![]() , starting from some initial guess of the state, denoted by
, starting from some initial guess of the state, denoted by ![]() .
.
So how to achieve this goal? We achieve this goal by properly designing the observer gain matrix ![]() . But, wait a second, what does it mean to properly design? We will answer these questions in the sequel.
. But, wait a second, what does it mean to properly design? We will answer these questions in the sequel.
Let us introduce the observer estimation error ![]() :
:
(10) ![]()
The main goal of the observer is achieved by designing the matrix ![]() such that asymptotically, the observer estimation error (10) approaches zero. Let us explain how to do that. Let us differentiate the equation (10)
such that asymptotically, the observer estimation error (10) approaches zero. Let us explain how to do that. Let us differentiate the equation (10)
(11) ![]()
By substituting ![]() from (8) and
from (8) and ![]() from (9) in (11), we obtain
from (9) in (11), we obtain
(12) 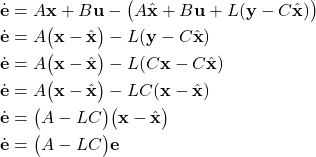
The last equation is obtained by using (10) and by using the fact that ![]() . The last equation is very important, and let us repeat it for clarity
. The last equation is very important, and let us repeat it for clarity
(13) ![]()
Now, the observer design problem is to design the matrix ![]() such that the system (13) is asymptotically stable. This is essentially the pole placement problem, that was analyzed and solved when we considered feedback control problems. That is, to design the observer gain matrix L, we will use the same pole placement method that is used for the control design. There is a complete mathematical equivalence or in control engineering terminology “duality” between observer design and feedback matrix design based on pole placement.
such that the system (13) is asymptotically stable. This is essentially the pole placement problem, that was analyzed and solved when we considered feedback control problems. That is, to design the observer gain matrix L, we will use the same pole placement method that is used for the control design. There is a complete mathematical equivalence or in control engineering terminology “duality” between observer design and feedback matrix design based on pole placement.
The goal is to design the matrix ![]() such that the poles of the closed-loop matrix
such that the poles of the closed-loop matrix ![]() have negative real parts and they are placed at the desired locations specified by the control designer. We can use Ackermann’s formula to solve this problem. However, since this is an introductory tutorial, we will not explain Ackermann’s formula. Instead, we will use Python to solve the pole placement problem and the function place() implemented in Python’s Control Systems Library. You can also use MATLAB’s function place to assign the observer poles.
have negative real parts and they are placed at the desired locations specified by the control designer. We can use Ackermann’s formula to solve this problem. However, since this is an introductory tutorial, we will not explain Ackermann’s formula. Instead, we will use Python to solve the pole placement problem and the function place() implemented in Python’s Control Systems Library. You can also use MATLAB’s function place to assign the observer poles.
Before we present a Python script for designing and simulating the observer algorithm. We need to address the following question.
Where to place the observer poles?
There are two schools of thought and two different opinions related to this important question.
- The observer poles must be two to five times faster than the feedback control poles in order to ensure that the observer estimation error (10) converges to zero much quicker than the control inputs. That is, we want our observer to quickly obtain a good estimate of the true system state, such that this state can be used in the state feedback control algorithm. Since in this case, the feedback control poles are slower than the observer poles, the closed-loop dynamics is primarily determined by the closed-loop control poles.
- The issue with the first approach is that in the presence of considerable noise and process disturbances, the fast dynamics of the observer closed loop poles can amplify the noise and disturbances. You can see that from the observer equation (9). The output of the system
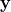 influences the observer correction term, and consequently, the measurement noise that is present in
influences the observer correction term, and consequently, the measurement noise that is present in 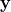 will affect the observer behavior. In this case, it is a good idea to explore the possibility of placing the observer poles such that they are slower than the feedback control poles. By doing this, the response of the system will be dominated by the observer poles and we will decrease the bandwidth of the system, thus making the system less sensitive to noise. Another approach is to design a low pass or a notch filter that will filter the output of the system
will affect the observer behavior. In this case, it is a good idea to explore the possibility of placing the observer poles such that they are slower than the feedback control poles. By doing this, the response of the system will be dominated by the observer poles and we will decrease the bandwidth of the system, thus making the system less sensitive to noise. Another approach is to design a low pass or a notch filter that will filter the output of the system 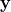 , and then, use that filtered output in the observer equation (9) instead of
, and then, use that filtered output in the observer equation (9) instead of 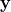 .
.
Observer Design By Using Pole Placement and Observer Design and Simulation in Python
Over here, we explain how to design the observer gain matrix ![]() by using the pole placement method. We explain the main ideas on how to implement the solution in Python. The complete Python simulation codes are given here (the small fee is used to support this website).
by using the pole placement method. We explain the main ideas on how to implement the solution in Python. The complete Python simulation codes are given here (the small fee is used to support this website).
Let ![]() be a vector whose elements are desired observer closed-loop poles. That is, this vector contains complex numbers that are desired poles of the observer closed-loop matrix
be a vector whose elements are desired observer closed-loop poles. That is, this vector contains complex numbers that are desired poles of the observer closed-loop matrix ![]() . For example, in our case, this set can be
. For example, in our case, this set can be
(14) 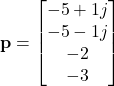
When defining the vector of desired pole locations, we need to keep in mind that if we specify a complex pole location, then we also need to have a conjugate pole that is symmetric with respect to the real axis.
To perform the pole placement, we use the Python Control Systems Library. In particular, we use the function place(). This function computes the matrix ![]() , such that the closed-loop control matrix
, such that the closed-loop control matrix
(15) ![]()
has poles at prescribed locations. This function is used like this “place(A,B,p)”, where p is the list of desired poles (in our case the vector (14) ), and it returns the matrix ![]() .
.
Now, how can we use this function to assign the poles of the closed-loop observer matrix ![]() ? We cannot directly use this function since this matrix is not in the correct form necessary to use the function. However, we can still use this function with several modifications of the input arguments.
? We cannot directly use this function since this matrix is not in the correct form necessary to use the function. However, we can still use this function with several modifications of the input arguments.
First of all, it is a very-well known fact that a square matrix and its transpose have the same set of eigenvalues. Consequently, the matrix
(16) ![]()
and its transpose given by
(17) ![]()
have identical eigenvalues. This means that we can assign the closed loop poles of (17) and these closed-loop poles will exactly be the closed loop poles of (16). It should be overved that the matrix ![]() is in the structurally identical form to the matrix
is in the structurally identical form to the matrix ![]() that is used by the function “place()”. Consequently, by typing “place(A^{T},C^{T},p)” in Python, we will compute the matrix
that is used by the function “place()”. Consequently, by typing “place(A^{T},C^{T},p)” in Python, we will compute the matrix ![]() . Then, we will just take the transpose of the matrix
. Then, we will just take the transpose of the matrix ![]() to obtain our matrix
to obtain our matrix ![]() . That is it. For more details see the YouTube video tutorial and the Python code files.
. That is it. For more details see the YouTube video tutorial and the Python code files.
Next, we need to explain how to simulate the computed observer. Let us look again at the observer equation
(18) ![]()
We can write this equation like this
(19) ![]()
This is a state equation, with
- the state matrix
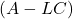
- input matrix
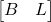
- the input vector
(20)
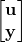
By simulating the original system (3) for the known input ![]() , we can obtain the time sequences of
, we can obtain the time sequences of ![]() and
and ![]() . Then, we can use the input
. Then, we can use the input ![]() and the output
and the output ![]() as inputs in (19) to simulate the state equation of the observer. This can be done in Python by using the Python Control System Library function “forced_response()” which is very similar to MATLAB’s function “lsim()”. For more details on how to simulate the observer in Python see the developed Python code files that come with this tutorial.
as inputs in (19) to simulate the state equation of the observer. This can be done in Python by using the Python Control System Library function “forced_response()” which is very similar to MATLAB’s function “lsim()”. For more details on how to simulate the observer in Python see the developed Python code files that come with this tutorial.
The system and observer simulations are given below. The first graph given below shows the step response of the system to the constant force equal to ![]() . We plot the position of the first object (state variable
. We plot the position of the first object (state variable ![]() ), where we assumed an arbitrary initial condition for simulation.
), where we assumed an arbitrary initial condition for simulation.
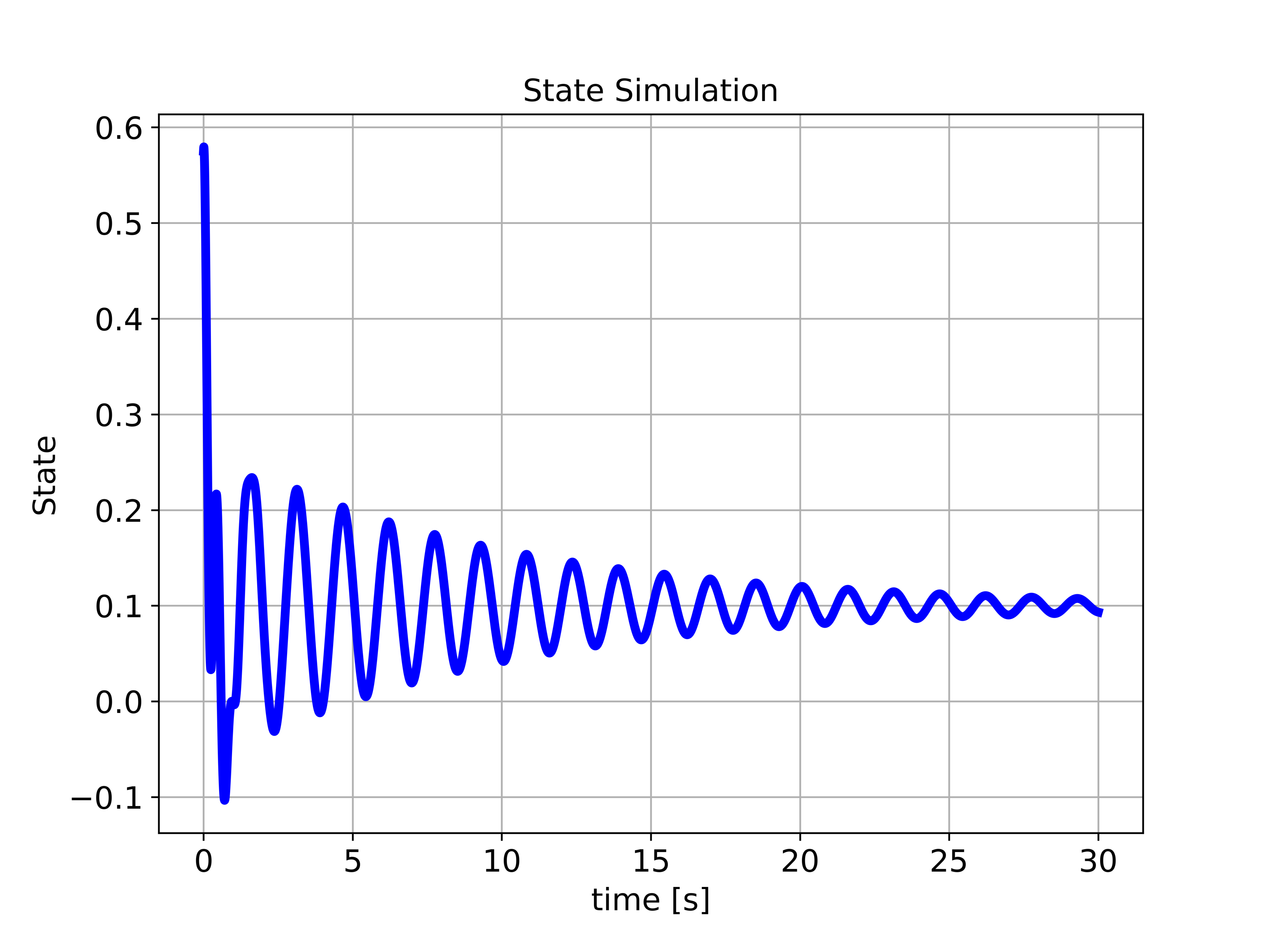
![Rendered by QuickLaTeX.com 10[N]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-ad63ed9a6de7986dc1ff95983295af72_l3.png) . This response shows the position of the first object over time.
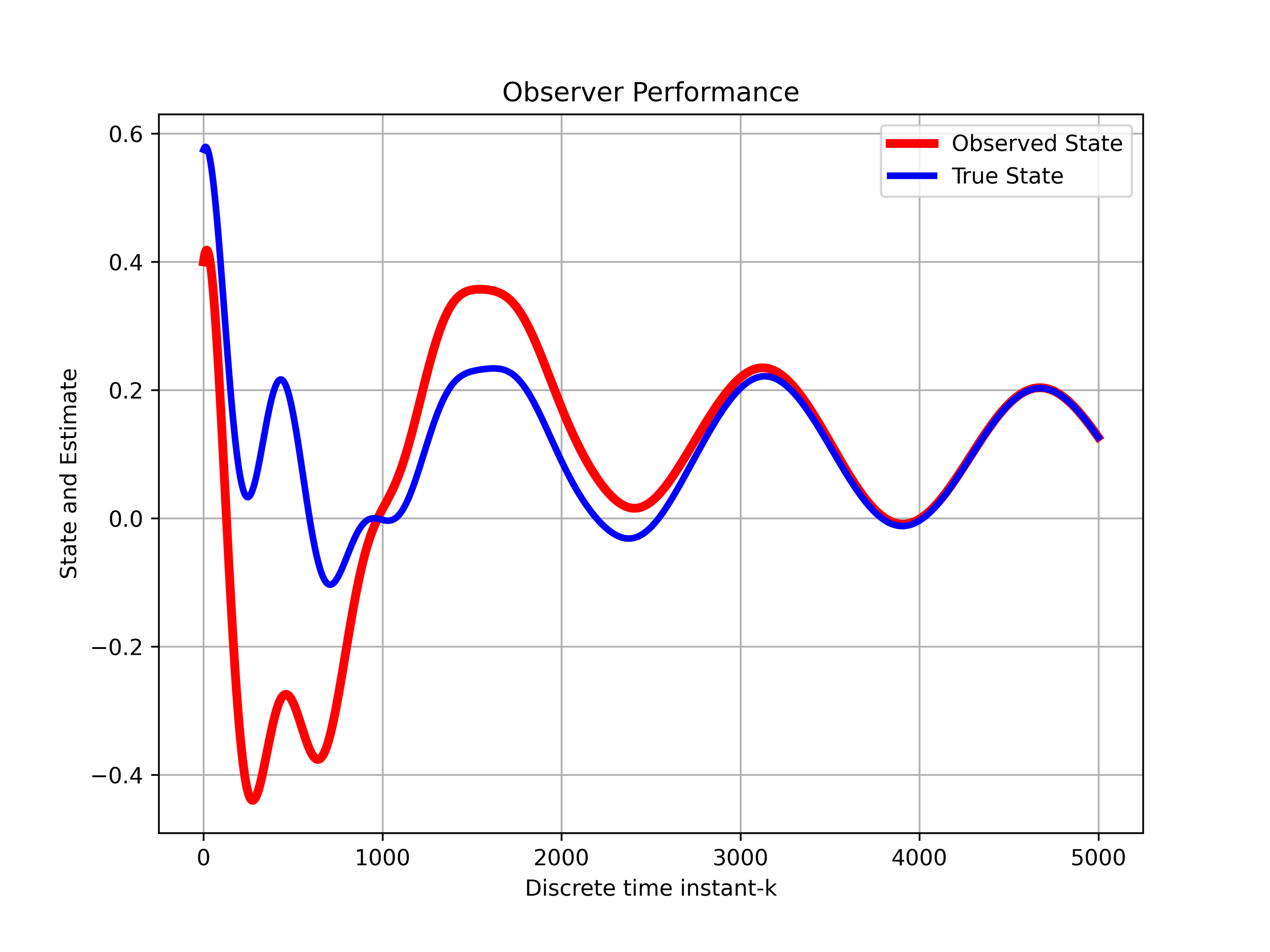
. This response shows the position of the first object over time.The figure below shows the convergence of the observer. We assumed an arbitrary initial condition of the observer. That is, we assumed an arbitrary initial guess of the state. The time behavior of the observer state variable ![]() and the true system state variable
and the true system state variable ![]() (position of the first object) is shown in the figure below.
(position of the first object) is shown in the figure below.
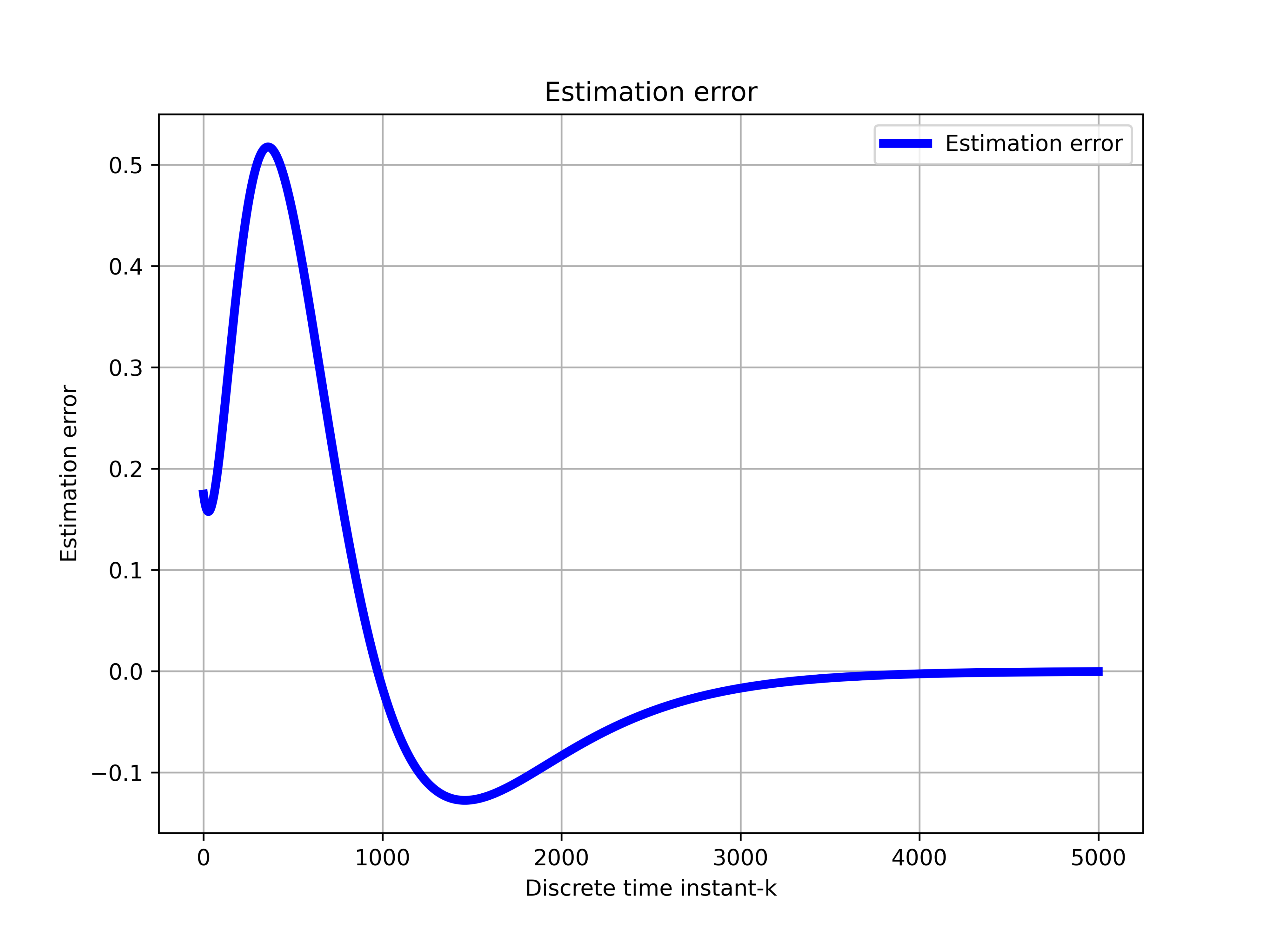
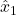 and the true system state variable
and the true system state variable 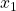
We can observe that the state estimate ![]() asymptotically converges to
asymptotically converges to ![]() . Initially, we do not have any knowledge about the state, and consequently, the observer starts from a random guess of the state estimate. As time progresses, and more output measurements of the system are filtered by the observer, we get better and better state estimates. This means that the observer is properly designed. The figure below shows the state estimation error
. Initially, we do not have any knowledge about the state, and consequently, the observer starts from a random guess of the state estimate. As time progresses, and more output measurements of the system are filtered by the observer, we get better and better state estimates. This means that the observer is properly designed. The figure below shows the state estimation error ![]() of the variable
of the variable ![]() as the function of time. We can observe that the state estimation error approaches zero. This also confirms the asymptotic stability of the observer.
as the function of time. We can observe that the state estimation error approaches zero. This also confirms the asymptotic stability of the observer.
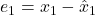 of the variable
of the variable 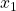 as the function of time.
as the function of time.