In this digital signal processing and control engineering tutorial, we provide a clear and graphical explanation of the convolution operator which is also known as the convolution sum or simply as convolution. Signal convolution is a fundamental operation in signal processing, control theory, machine learning, and time series prediction. Consequently, it is of paramount importance to understand the mechanism behind signal convolution and to properly understand how to compute signal convolution in MATLAB. All this is explained in this tutorial. The YouTube page accompanying this tutorial is given below.
Definition of Convolution Sum Operator
Let ![]() and
and ![]() be two scalar discrete-time signals, and let
be two scalar discrete-time signals, and let ![]() be a discrete-time instant. Then, convolution of
be a discrete-time instant. Then, convolution of ![]() and
and ![]() is defined as follows
is defined as follows
(1) ![Rendered by QuickLaTeX.com \begin{align*}y[n]=\sum_{k=-\infty}^{+\infty}x[k]h[n-k]\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-f5f50bfa7c4ae5f6d20134c37f307a22_l3.png)
where ![]() is another discrete-time signal that is determined by the convolution. Often in literature, the convolution (convolution sum operator) is denoted by the start operator “
is another discrete-time signal that is determined by the convolution. Often in literature, the convolution (convolution sum operator) is denoted by the start operator “![]() “. Consequently, convolution can be written like this
“. Consequently, convolution can be written like this
(2) ![Rendered by QuickLaTeX.com \begin{align*}y[n]=x[n]\ast h[n]= \sum_{k=-\infty}^{+\infty}x[k]h[n-k]\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-01b5eaa0485eb6d6e668191cf906b01d_l3.png)
In the theory of discrete dynamical systems, the signal ![]() is often the impulse response of a linear dynamical time-invariant system, and
is often the impulse response of a linear dynamical time-invariant system, and ![]() is the discrete-time input signal. In that case, convolution (2) defines a response of the discrete-time system to the input
is the discrete-time input signal. In that case, convolution (2) defines a response of the discrete-time system to the input ![]() . That is, the response of the system is completely determined by the impulse response and the input signal. This is a very important fact in linear system theory.
. That is, the response of the system is completely determined by the impulse response and the input signal. This is a very important fact in linear system theory.
In many cases, the signal ![]() is zero for negative values of
is zero for negative values of ![]() . In that case, we can expand the sum as follows
. In that case, we can expand the sum as follows
(3) ![]()
Let us write this sum until the term ![]()
(4) ![]()
The best approach for understanding convolution is to consider an example. Consequently, let us consider the following example.
Example demonstrating convolution: Let the signals ![]() and
and ![]() be defined as follows
be defined as follows
(5) ![Rendered by QuickLaTeX.com \begin{align*}h[n] = \left\{ \begin{array}{ll} 3 & , \;\; n=0 \\ 2 &, \;\; n=1 \\ 1 &, \;\; n=2 \\ 0 &, \;\; \text{for all other integer} \;\; n \end{array} \right.\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-52eee092b35d3af5ceb9f2982d6a225a_l3.png)
(6) ![Rendered by QuickLaTeX.com \begin{align*}x[n] = \left\{ \begin{array}{ll} 1 & , \;\; n=0 \\ 2 &, \;\; n=1 \\ 3 &, \;\; n=2 \\ 0 &, \;\; \text{for all other integer} \;\; n \end{array} \right.\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-f8d4c59a485fef60d9d0dce666941a4f_l3.png)
Compute the convolution sum
(7) ![Rendered by QuickLaTeX.com \begin{align*}y[n]=\sum_{k=-\infty}^{+\infty}x[k]h[n-k]\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-6c17311dba44155fc1bbe758acd3f925_l3.png)
and give a graphical interpretation and derive a graphical method for computing the convolution sum.
Solution:
The figure below shows a graphical representation of two signals
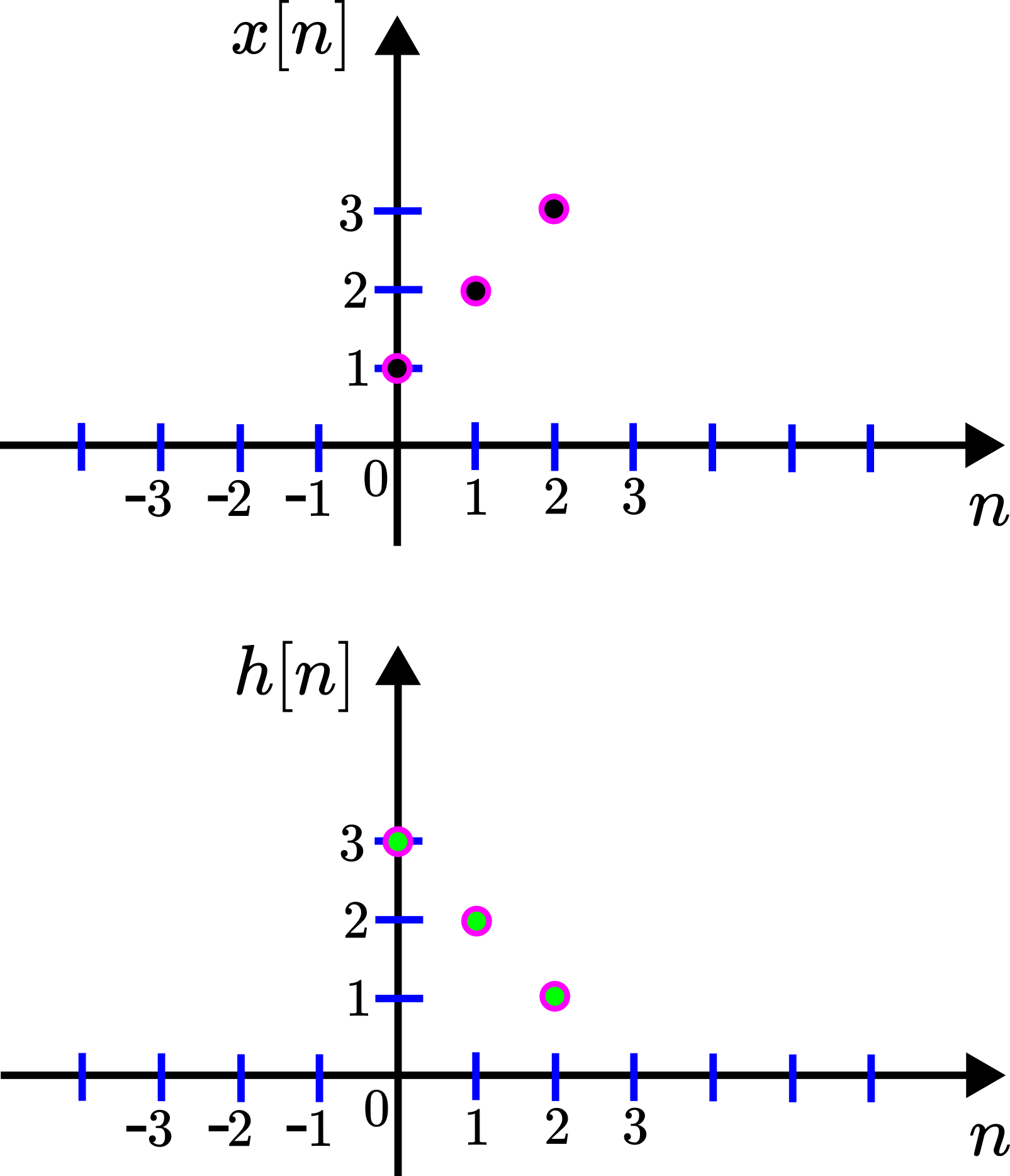
First, taking into account that ![]() for negative values of
for negative values of ![]() , the sum (7) takes the following form
, the sum (7) takes the following form
(8) ![Rendered by QuickLaTeX.com \begin{align*}y[n] & =\sum_{k=0}^{+\infty}x[k]h[n-k] \\y[n] & =x[0]h[n]+x[1]h[n-1]+x[2]h[n-2]+x[3]h[n-3]+\ldots \end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-54f0dcc744efd7134f874c1357461b16_l3.png)
Now, taking into account that ![]() only for
only for ![]() , the convolution sum (8) takes the following form
, the convolution sum (8) takes the following form
(9) ![]()
Let us now represent this sum for different values of ![]() . For
. For ![]() , we have
, we have
(10) ![Rendered by QuickLaTeX.com \begin{align*}y[0] &=x[0]h[0]+x[1]h[-1]+x[2]h[-2] \\& = x[0]h[0]+x[1]0+x[2]0 \\& =x[0]h[0] =1\cdot 3=3\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-6a4864e320a0fc4cba27d8d6d3926882_l3.png)
For ![]() , we have
, we have
(11) ![Rendered by QuickLaTeX.com \begin{align*}y[1]& =x[0]h[1]+x[1]h[0]+x[2]h[-1] \\& =x[0]h[1]+x[1]h[0]+x[2]0 \\& =x[0]h[1]+x[1]h[0] =1\cdot 2 +2\cdot 3 = 8 \end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-60f797d8681983e54703148b6a49651c_l3.png)
For ![]() , we have
, we have
(12) ![]()
For ![]() , we have
, we have
(13) ![Rendered by QuickLaTeX.com \begin{align*}y[3]& =x[0]h[3]+x[1]h[2]+x[2]h[1]\\& =x[0]\cdot 0 +x[1]h[2]+x[2]h[1] \\& = x[1]h[2]+x[2]h[1] =2 \cdot 1+ 3 \cdot 2 = 8 \end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-a60d2a1db27aa0ab0bf8e36502190f0a_l3.png)
For ![]() , we have
, we have
(14) ![Rendered by QuickLaTeX.com \begin{align*}y[4] & =x[0]h[4]+x[1]h[3]+x[2]h[2] \\& =x[0]\cdot 0+x[1]\cdot 0+x[2]h[2] \\& = x[2]h[2] =3\cdot 1 = 3\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-d5a11ca35357af710bb272a7d4d97d70_l3.png)
To give a graphical interpretation of the convolution sum, let us analyze again the derived equations
(15) ![Rendered by QuickLaTeX.com \begin{align*}& n=0,\;\; y[0]=x[0]h[0]+x[1]h[-1]+x[2]h[-2] \\& n=1,\;\; y[1]=x[0]h[1]+x[1]h[0]+x[2]h[-1] \\& n=2,\;\; y[2]=x[0]h[2]+x[1]h[1]+x[2]h[0] \\& n=3,\;\; y[3]=x[0]h[3]+x[1]h[2]+x[2]h[1] \\& n=4,\;\; y[4]=x[0]h[4]+x[1]h[3]+x[2]h[2]\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-9f02c0615c3baef30ebc63f54d2fa03a_l3.png)
We can observe the following
- In the sum terms, the position of the sequence
![Rendered by QuickLaTeX.com x[n]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-7678456914fac638e67ac10b23409f76_l3.png) stays the same as
stays the same as 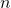 is increased.
is increased. - In the sum terms, the sequence
![Rendered by QuickLaTeX.com h[n]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-01c00f0d13881e00029fc918e67d81cc_l3.png) is shifted in time at corresponding positions in the sum.
is shifted in time at corresponding positions in the sum.
This means that in the graphical interpretation of the convolution sum, the sequence ![]() is fixed, and the sequence
is fixed, and the sequence ![]() is shifted. However, the sequence
is shifted. However, the sequence ![]() has to be reversed or reflected with respect to the vertical axis. This is explained in the sequel. For that purpose, and for clarity, let us again write the general formula (9) as follows
has to be reversed or reflected with respect to the vertical axis. This is explained in the sequel. For that purpose, and for clarity, let us again write the general formula (9) as follows
(16) ![Rendered by QuickLaTeX.com \begin{align*}y[n]=x[0]h[n]+x[1]h[n-1]+x[2]h[n-2]=\sum_{k=0}^{2}x[k]h[n-k]\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-3b3abf9dcb2ccf56870157bf58e996f1_l3.png)
From this formula, we have
(17) ![Rendered by QuickLaTeX.com \begin{align*}& n=0,\;\; y[0]=x[0]h[0-0]+x[1]h[0-1]+x[2]h[0-2]=\sum_{k=0}^{2}x[k]h[0-k] \\& n=1,\;\; y[1]=x[0]h[1-0]+x[1]h[1-1]+x[2]h[1-2]=\sum_{k=0}^{2}x[k]h[1-k] \\& n=2,\;\; y[2]=x[0]h[2-0]+x[1]h[2-1]+x[2]h[2-2]=\sum_{k=0}^{2}x[k]h[2-k] \\& n=3,\;\; y[3]=x[0]h[3-0]+x[1]h[3-1]+x[2]h[3-2]=\sum_{k=0}^{2}x[k]h[3-k] \\& n=4,\;\; y[4]=x[0]h[4-0]+x[1]h[4-1]+x[2]h[4-2]=\sum_{k=0}^{2}x[k]h[4-k]\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-aeba5bdbfbfef8475d4f0282074858b5_l3.png)
In these sums, we can think of the sequence ![]() ,
, ![]() , as the sequence
, as the sequence ![]() that is shifted (delayed) for
that is shifted (delayed) for ![]() time steps.
time steps.
Let us further elaborate on how the sequence ![]() is constructed from the sequence
is constructed from the sequence ![]() or
or ![]() . Let us denote the sequence
. Let us denote the sequence ![]() by
by ![]() . That is,
. That is,
(18) ![]()
Taking into account the definition of the sequence ![]() , for
, for ![]() , the sequence
, the sequence ![]() is
is
(19) ![Rendered by QuickLaTeX.com \begin{align*}k=0,\; => \; h_{1}[0]=h[0]=3 \\k=-1,\; => \;h_{1}[-1]= h[-(-1)]=h[1]=2 \\k=-2,\; => \; h_{1}[-2]= h[-(-2)]=h[2]=1 \\\text{for all other values of} \;\; k \;\; =>\; h_{1}[k]=h[-k]=0\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-a26bcf2ef00d50ade7373287b2224e2e_l3.png)
This is actually the original sequence ![]() that is mirrored or reflected with respect to the vertical axis
that is mirrored or reflected with respect to the vertical axis ![]() . This sequence is illustrated in the figure below.
. This sequence is illustrated in the figure below.
![Rendered by QuickLaTeX.com h[-k]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-028d8cbe0e5a5bace50c828be29c8da0_l3.png) .
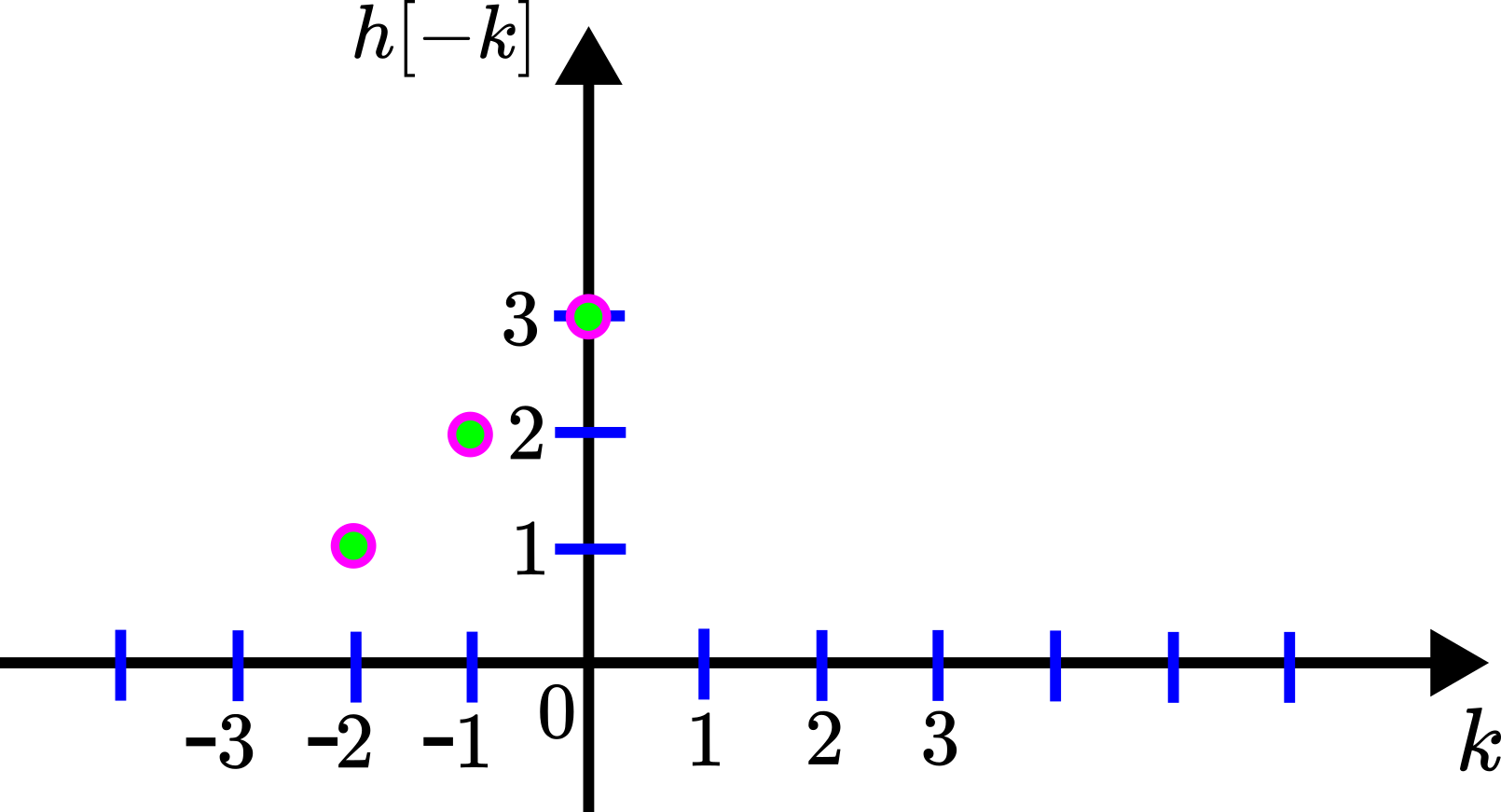
.If we delay or shift this sequence in time, we will obtain the following sequences for different values of the time delay:
![Rendered by QuickLaTeX.com h[-k]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-028d8cbe0e5a5bace50c828be29c8da0_l3.png) delayed for
delayed for 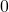 ,
, 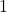 ,
, 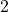 , and
, and 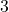 time steps.
time steps.These shifted or delayed sequences constructed on the basis of ![]() , will help us to graphically interpret the convolution sum.
, will help us to graphically interpret the convolution sum.
Let us start with ![]()
(20) ![]()
This sum has the graphical interpretation given in the figure below.
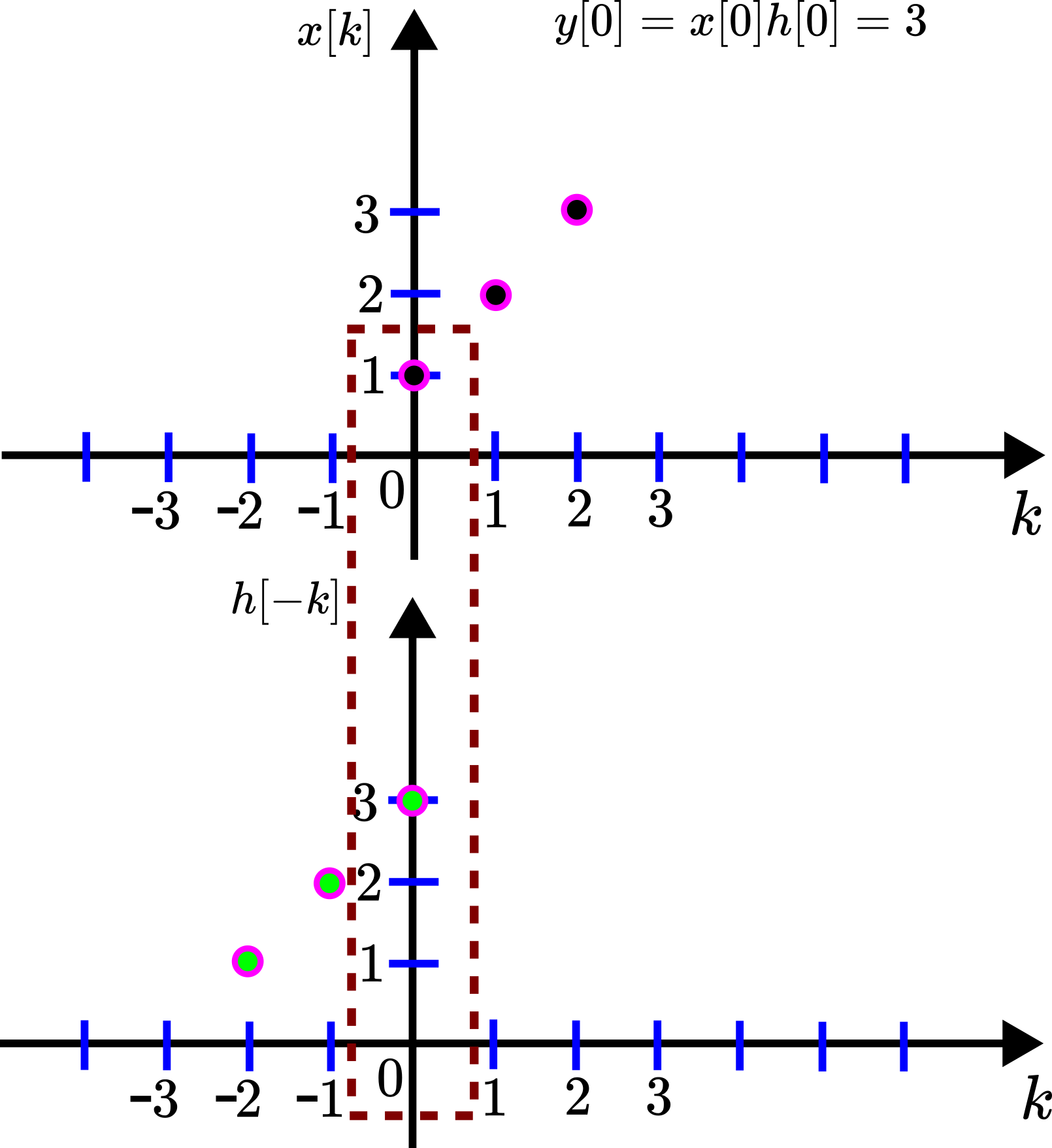
![Rendered by QuickLaTeX.com y[0]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-303eaebff2cb2159ebc878229caa4eed_l3.png) .
.We only multiply the terms of the sequences ![]() and
and ![]() that are in the dashed rectangle.
that are in the dashed rectangle.
For ![]() , we have
, we have
(21) ![]()
This sum has the graphical interpretation given in the figure below.
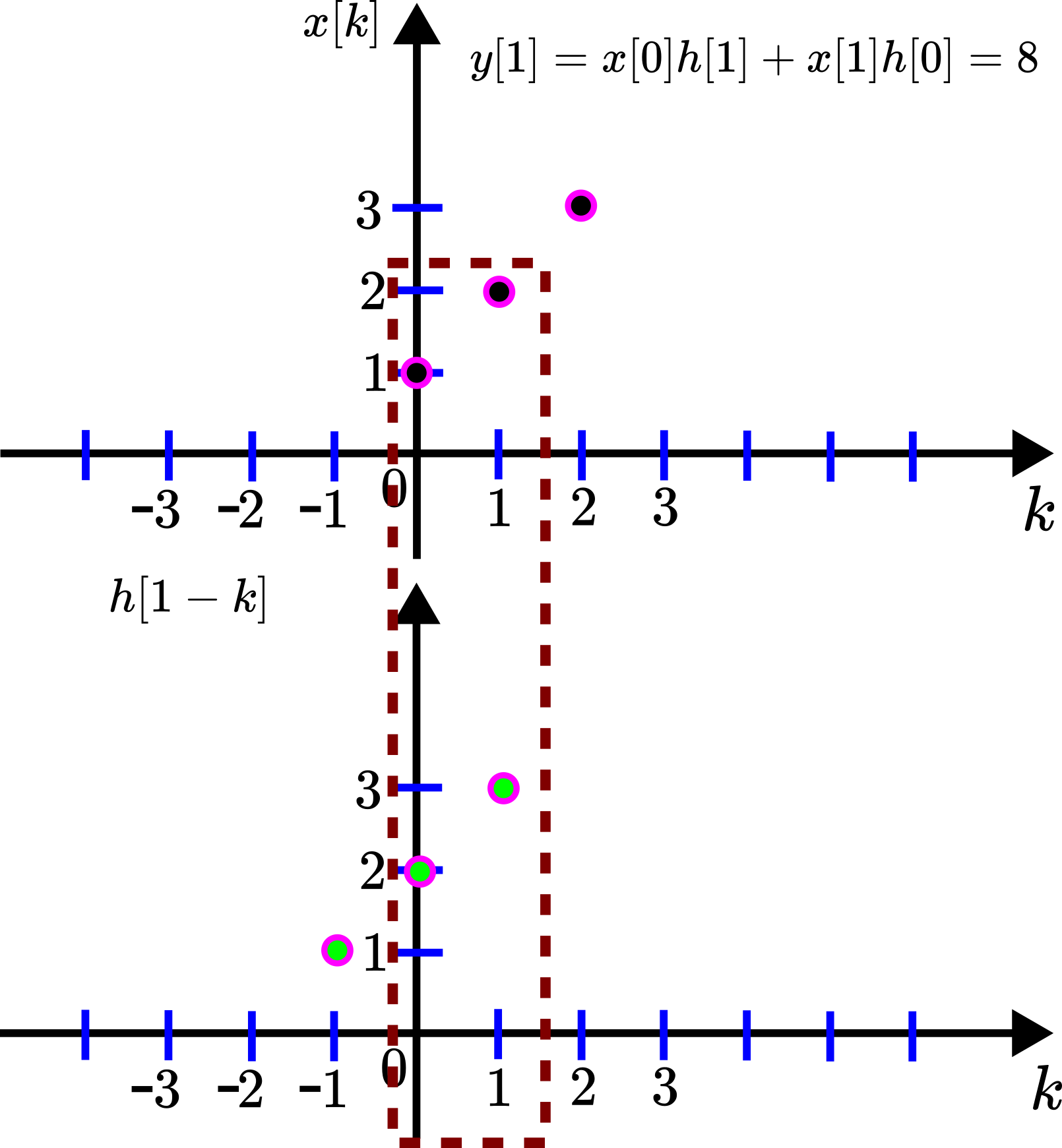
![Rendered by QuickLaTeX.com y[1]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-5c130d8a2453ab754d4f44b240ec527e_l3.png) .
.We delay the sequence ![]() to obtain
to obtain ![]() , and we only multiply the terms of the sequences
, and we only multiply the terms of the sequences ![]() and
and ![]() that are in the dashed rectangle.
that are in the dashed rectangle.
For ![]() , we have
, we have
(22) ![]()
This sum has the graphical interpretation given in the figure below.
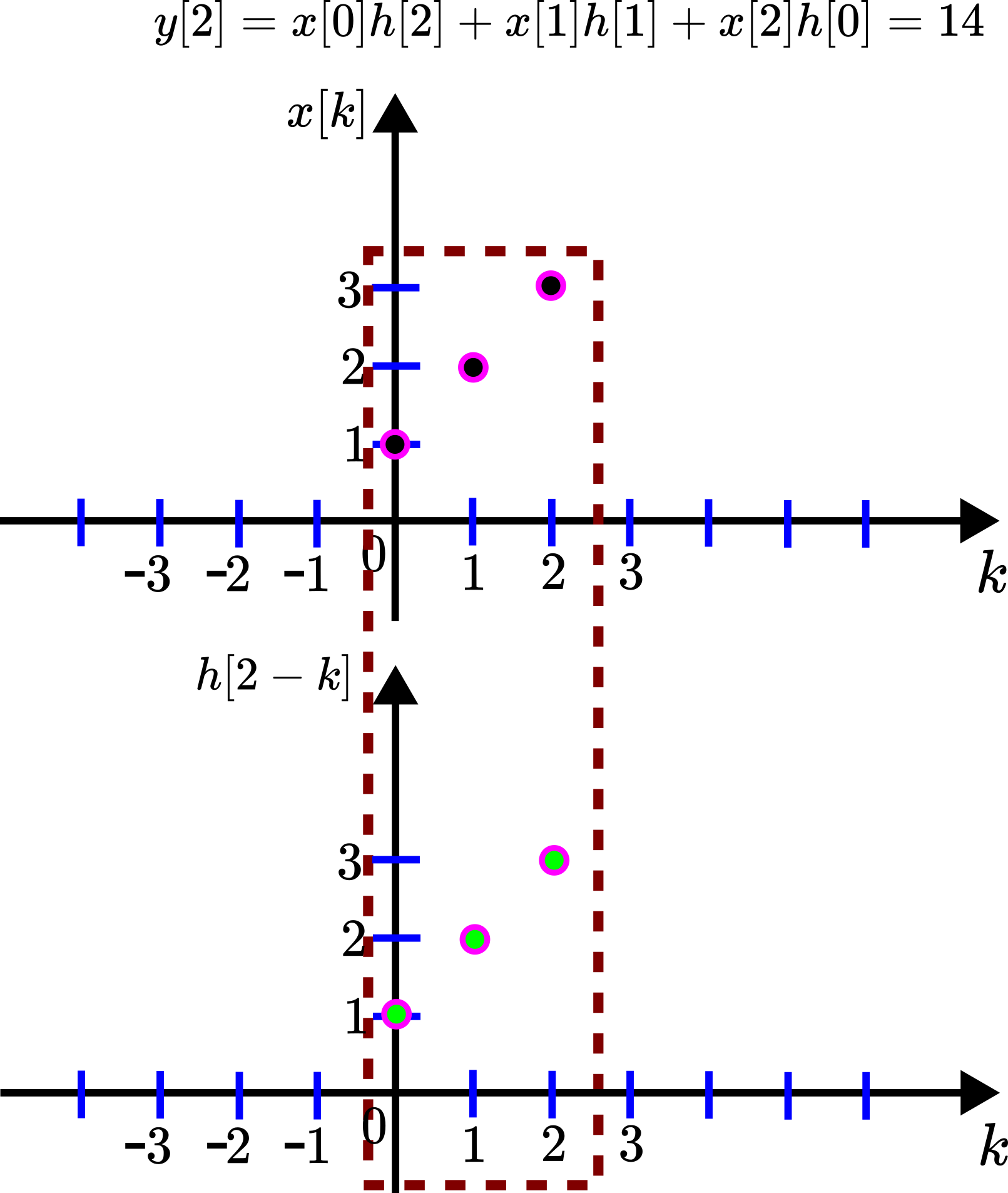
![Rendered by QuickLaTeX.com y[2]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-80430bda773bf7cb6ca603292b7c979c_l3.png) .
.We delay the sequence ![]() to obtain
to obtain ![]() , and we only multiply the terms of the sequences
, and we only multiply the terms of the sequences ![]() and
and ![]() that are in the dashed rectangle.
that are in the dashed rectangle.
For ![]() , we have
, we have
(23) ![]()
This sum has the graphical interpretation given in the figure below.
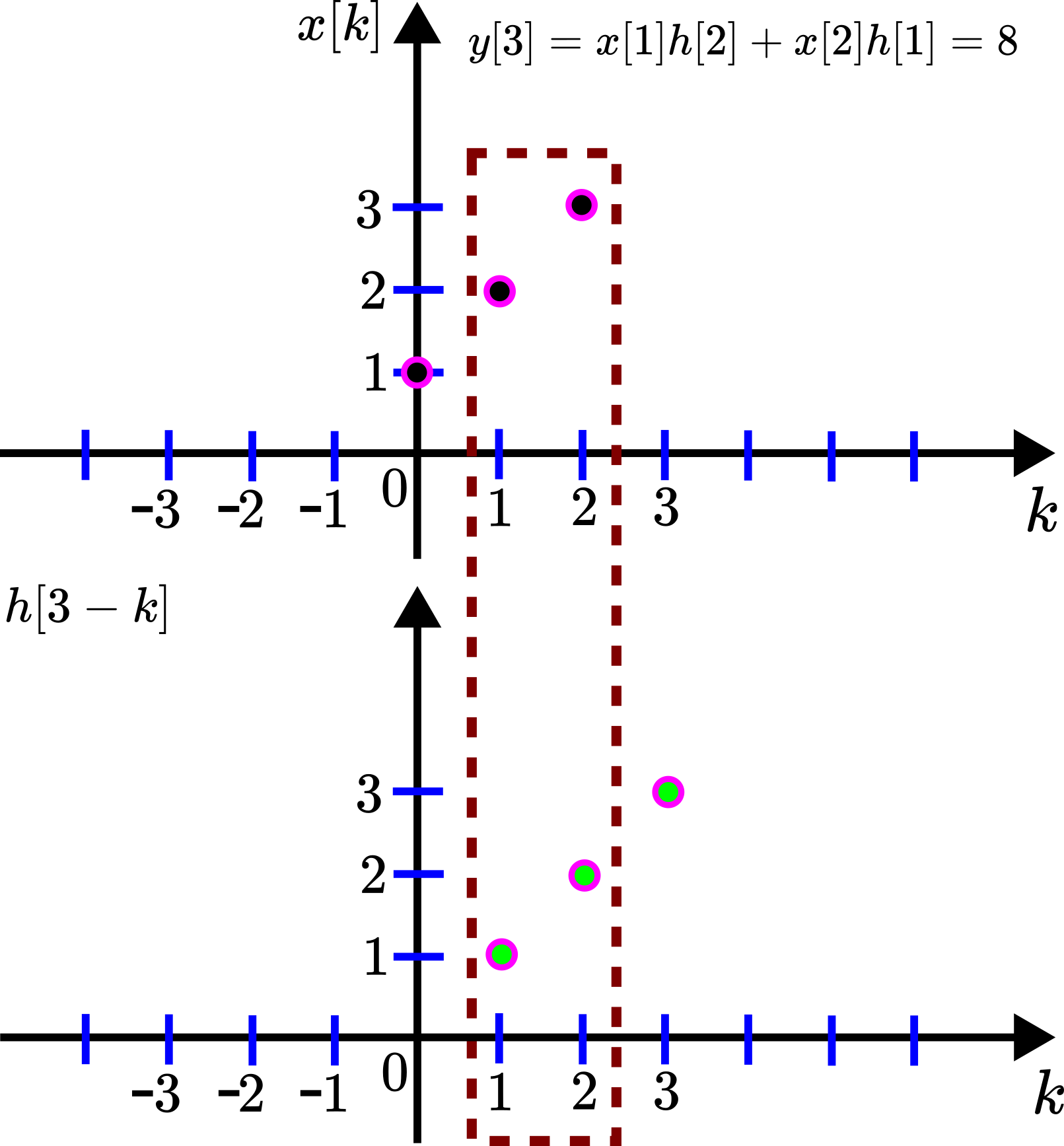
![Rendered by QuickLaTeX.com y[3]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-0fa142f298bea8e6a16d4376658755a1_l3.png) .
.We delay the sequence ![]() to obtain
to obtain ![]() , and we only multiply the terms of the sequences
, and we only multiply the terms of the sequences ![]() and
and ![]() that are in the dashed rectangle.
that are in the dashed rectangle.
For ![]() , we have
, we have
(24) ![]()
This sum has the graphical interpretation given in the figure below.
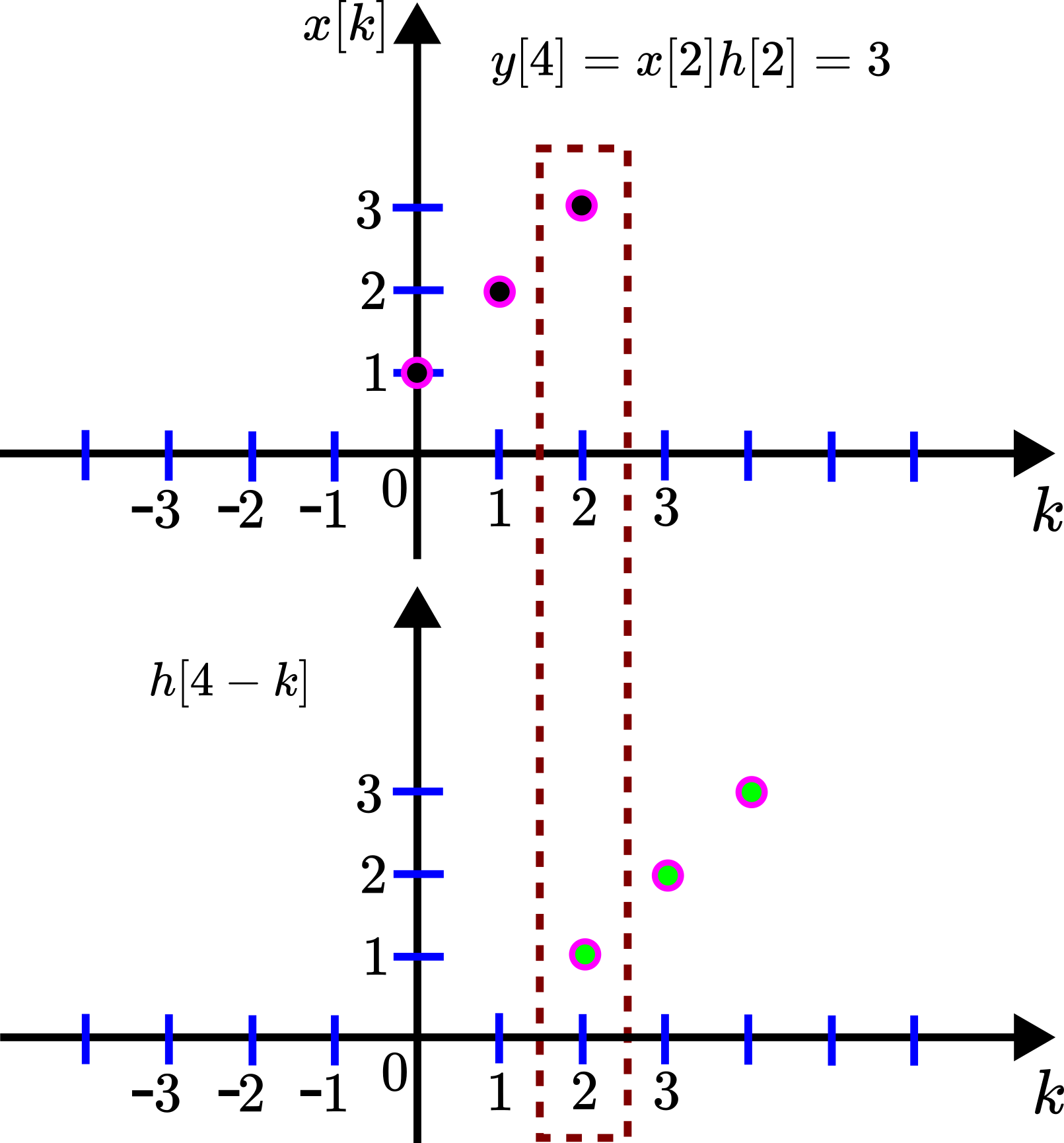
![Rendered by QuickLaTeX.com y[4]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-58cd652f501eca4f303f36c7dbcec9c3_l3.png) .
.We delay the sequence ![]() to obtain
to obtain ![]() , and we only multiply the terms of the sequences
, and we only multiply the terms of the sequences ![]() and
and ![]() that are in the dashed rectangle.
that are in the dashed rectangle.
Convolution in MATLAB
The following MATLAB script will compute convolution
x = [1 2 3];
h = [3 2 1];
y = conv(x,h,'full')The output is
y =
3 8 14 8 3We used the MATLAB function conv() to compute the convolution. The MATLAB script is self-explanatory.