In this control engineering and robotics tutorial, we explain the basics of position controllers for mobile robots. As a test case, we use a differential drive robot. Differential drive robots are also called differential wheeled robots. We design a simple proportional controller that will drive the robot center from the initial to the desired location. We use a kinematics robot model developed in our previous tutorial to simulate the robot’s motion. We explain how to generate a 2D Pygame animation that simulates the robot’s motion and control performance. Here, it should be kept in mind that we develop a controller that is based on the kinematics of the robot without taking into account the robot’s dynamics described by mass, moments of inertia, and dynamics equations. The Python scripts used to implement the control algorithm and to simulate robot motion are available here.
The YouTube tutorial accompanying this post is given below.
Differential Drive Robot Position Controller
Here, we first briefly summarize the kinematics diagram and the kinematics differential equation model of the robot. For details, see our previous tutorial given here. The robot kinematic diagram is shown below.
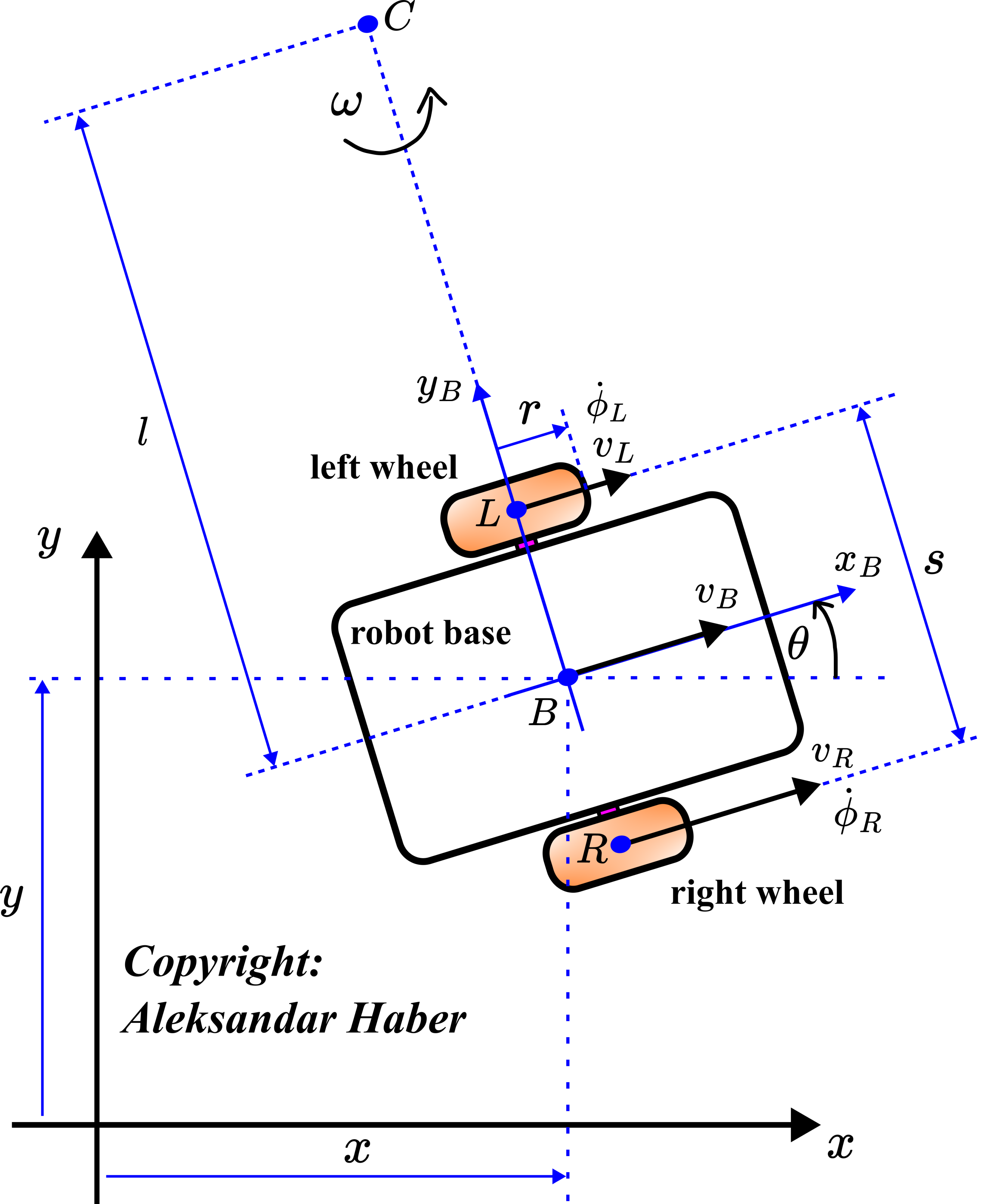
The symbols used in this figure are explained below.
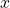 and
and 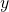 are the translation coordinates of the body frame attached to the point
are the translation coordinates of the body frame attached to the point  with respect to the inertial frame
with respect to the inertial frame 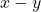 .
.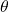 is the angle of rotation of the robot which is at the same time the angle between the body frame and the inertial frame.
is the angle of rotation of the robot which is at the same time the angle between the body frame and the inertial frame. 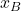 and
and 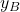 are the coordinates in the body frame and at the same time they denote the axes of the body frame.
are the coordinates in the body frame and at the same time they denote the axes of the body frame. 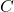 is the instantaneous center of rotation.
is the instantaneous center of rotation. is the instantaneous angular velocity of the robot body.
is the instantaneous angular velocity of the robot body. 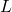 is the center point of the left wheel.
is the center point of the left wheel. 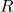 is the center point of the right wheel.
is the center point of the right wheel. is the middle point between the points
is the middle point between the points 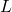 and
and 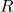 .
.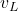 is the velocity of the center of the left wheel.
is the velocity of the center of the left wheel. 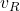 is the velocity of the center of the right wheel.
is the velocity of the center of the right wheel. 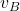 is the velocity of the point
is the velocity of the point  .
.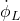 is the angular velocity of the left wheel.
is the angular velocity of the left wheel. 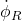 is the angular velocity of the right wheel.
is the angular velocity of the right wheel. 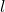 is the distance between the point
is the distance between the point  and the point
and the point 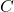 .
. is the radius of the wheels.
is the radius of the wheels. is the distance between the points
is the distance between the points 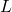 and
and 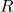 .
.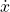 is the projection of the velocity
is the projection of the velocity 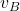 on the
on the 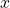 axis.
axis. 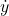 is the projection of the velocity
is the projection of the velocity 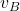 on the
on the 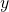 axis.
axis.
The kinematics system of differential equations describing the robot motion is given below (for more details, see our previous tutorial, given here):
(1) 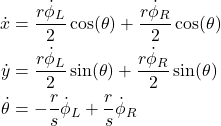
On the other hand, for the implementation of the control algorithm, we need another equation relating ![]() and
and ![]() with
with ![]() and
and ![]() . This equation is given below:
. This equation is given below:
(2) ![]()
The robot is controlled by controlling the left and right wheel angular velocities represented by ![]() and
and ![]() , respectively. For given values of
, respectively. For given values of ![]() and
and ![]() we can determine the robot position
we can determine the robot position ![]() and orientation
and orientation ![]() by integrating the system of equations (1).
by integrating the system of equations (1).
In this tutorial, we are mainly interested in driving the center of the robot ![]() to a desired (target or reference) location, without controlling the orientation
to a desired (target or reference) location, without controlling the orientation ![]() . That is, the robot can have an arbitrary orientation in the desired location. The control problem can be formally described as follows.
. That is, the robot can have an arbitrary orientation in the desired location. The control problem can be formally described as follows.
Control Problem Formulation: Let ![]() and
and ![]() be the
be the ![]() and
and ![]() coordinates of the desired (target or reference) location of the robot center
coordinates of the desired (target or reference) location of the robot center ![]() . Determine a sequence of wheel angular velocity control variables
. Determine a sequence of wheel angular velocity control variables ![]() and
and ![]() such that the current robot position
such that the current robot position ![]() is equal to the desired robot position
is equal to the desired robot position ![]() . Here, we assume that at any time instant, we can precisely measure the robot position
. Here, we assume that at any time instant, we can precisely measure the robot position ![]() and the robot orientation angle
and the robot orientation angle ![]() .
.
There are a number of approaches to solving this problem. Since this is an introductory tutorial, we will use a relatively simple approach based on a proportional controller. Here, the interested reader should keep in mind that this is NOT the most optimal controller that will optimize the travel distance, used energy, or a similar quantity.
The following diagram is instrumental in deriving the control algorithm
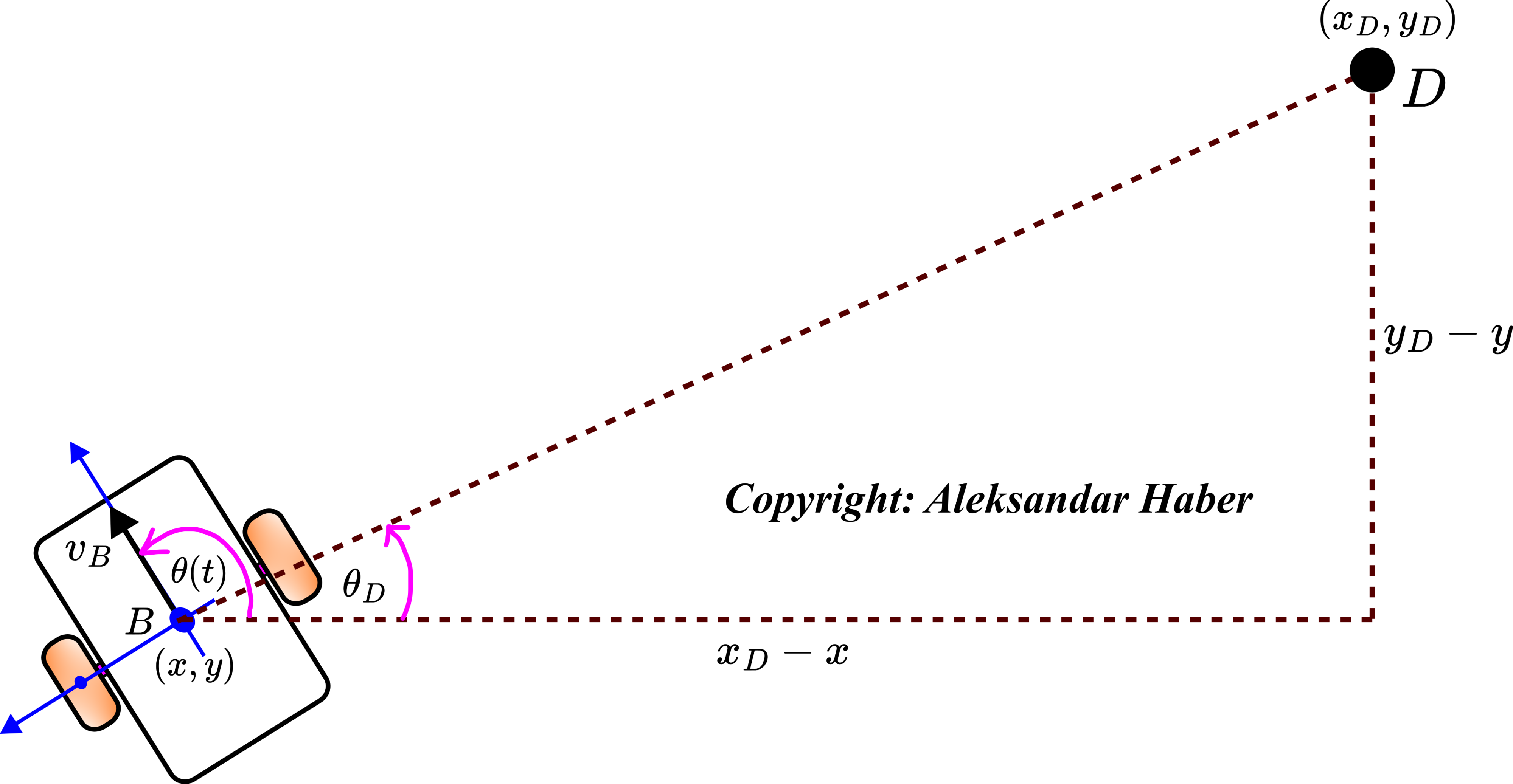
Let us suppose that at some time instant ![]() , the robot position is given by the coordinates
, the robot position is given by the coordinates ![]() and
and ![]() . Also, let us assume that at the time instant
. Also, let us assume that at the time instant ![]() , the orientation of the robot body is given by
, the orientation of the robot body is given by ![]() . Our goal is to steer the robot to the point
. Our goal is to steer the robot to the point ![]() with the coordinates
with the coordinates ![]() . We assume that the robot’s center has the velocity
. We assume that the robot’s center has the velocity ![]() .
.
Here, one important geometrical observation should be made. The velocity vector ![]() is tangent to the robot’s trajectory. Also, during a small time interval, this is the direction of the motion of the robot. To arrive at the target, we want to rotate this velocity vector such that it is in the direction of the line connecting the points
is tangent to the robot’s trajectory. Also, during a small time interval, this is the direction of the motion of the robot. To arrive at the target, we want to rotate this velocity vector such that it is in the direction of the line connecting the points ![]() and
and ![]() . That is, the angle
. That is, the angle ![]() should be equal to the angle
should be equal to the angle ![]() of the line connecting the points
of the line connecting the points ![]() and
and ![]() . By rotating the robot in this direction, we will achieve that the velocity is in the direction of the line connecting
. By rotating the robot in this direction, we will achieve that the velocity is in the direction of the line connecting ![]() and
and ![]() .
.
From the current robot’s position, we can calculate the desired orientation angle ![]() as follows
as follows
(3) ![]()
or
(4) ![]()
where the ![]() (or
(or ![]() ) is the modified
) is the modified ![]() or the 2-argument arctangent function that takes into account the signs of the arguments when computing the angles.
or the 2-argument arctangent function that takes into account the signs of the arguments when computing the angles.
The first controller is the controller that will change ![]() . We use the proportional controller that has the following form
. We use the proportional controller that has the following form
(5) ![]()
where ![]() is the current value of the orientation of the robot and
is the current value of the orientation of the robot and ![]() is the proportional control gain for orientation control.
is the proportional control gain for orientation control.
What is the physical meaning of the equation (5)? If the ![]() , then according to this equation
, then according to this equation ![]() and there is no change of
and there is no change of ![]() since we have achieved the desired robot orientation.
since we have achieved the desired robot orientation.
The orientation controller actually controls the angle of the velocity. However, we need a controller that will control the magnitude of the velocity. This controller will implicitly also control the position of the robot. The second controller has the following form
(6) ![]()
where ![]() is the proportional constant for controlling the robot’s velocity. This controller will change the intensity of the velocity. However, it will not change the direction of the velocity. The direction of the velocity vector is changed by the orientation controller (5). This controller penalizes the Euclidean distance between the point
is the proportional constant for controlling the robot’s velocity. This controller will change the intensity of the velocity. However, it will not change the direction of the velocity. The direction of the velocity vector is changed by the orientation controller (5). This controller penalizes the Euclidean distance between the point ![]() and the point
and the point ![]() . The larger the distance is, the larger the magnitude of the velocity
. The larger the distance is, the larger the magnitude of the velocity ![]() . As we get closer and closer to the desired location
. As we get closer and closer to the desired location ![]() , the intensity of the velocity
, the intensity of the velocity ![]() gradually decreases.
gradually decreases.
The controllers (5) and (6) determine the values of ![]() and
and ![]() . However, we need to control the angular velocities of the wheels
. However, we need to control the angular velocities of the wheels ![]() and
and ![]() . To control these angular velocities, we need to transform
. To control these angular velocities, we need to transform ![]() and
and ![]() into
into ![]() and
and ![]() . We can do that by inverting the system of equations (2). Namely, from this equation, we can express
. We can do that by inverting the system of equations (2). Namely, from this equation, we can express ![]() and
and ![]() as follows
as follows
(7) ![]()
That is, we invert the parameter matrix
(8) ![]()
Now, we are ready to summarize the control algorithm.
Summary of Control Algorithm for Differential Drive Robot
The control algorithm consists of the following steps.
- We observe the robot position
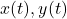 and the robot orientation
and the robot orientation 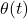
- We compute
(9)
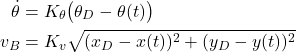
- We compute the desired angular wheel velocities
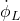 and
and 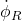 as follows
as follows(10)
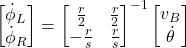
- Apply the computed values
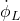 and
and 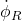 to the left and right wheel motor controllers that will generate the torques and move the wheels of the differential drive robot.
to the left and right wheel motor controllers that will generate the torques and move the wheels of the differential drive robot.
As mentioned at the beginning of this tutorial, we are not considering the dynamics of the robot. For us, the complete robot model is described by the kinematics equations (1). We are aware that this is an approximation, however, for robots with small masses and small moments of inertia this approximation can be sufficiently accurate to design the control inputs. Consequently, in our simulation, the model (1) serves as the “true” physical model of the robot. Over here, we write again these equations for clarity:
(11) 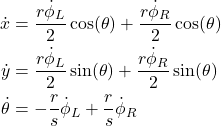
That is, in our simulations, once we compute ![]() and
and ![]() , we will use these quantities in the equation (11) as the known inputs. In our simulations, we integrate the system of equations (11) to compute the values of
, we will use these quantities in the equation (11) as the known inputs. In our simulations, we integrate the system of equations (11) to compute the values of ![]() and the robot orientation
and the robot orientation ![]() , and then we use these values in the step 1 of the control algorithm.
, and then we use these values in the step 1 of the control algorithm.
Python Simulation and Animation of Controller for Differential Drive Robot
We have developed Python codes for implementing the controller and for simulating the robot’s motion. We used Pygame to simulate the robot’s motion. The animations are shown in the video below. The Python scripts used to implement the control algorithm and to simulate robot motion are available here.