In this tutorial, we explain three must-know methods for computing Fibonacci sequences. By studying techniques for computing the Fibonacci sequences, you can learn the programming principles and way-of-thinking that can be applied to many different problems. The YouTube page accompanying this tutorial is given below. The code developed in this tutorial is also available on GitHub. Also, the code is summarized at the end of this post.
In this tutorial, we explain the following three approaches for computing Fibonacci sequences:
- The approach based on pure recursion (most inefficient approach).
- The approach based on vectors (more efficient approach).
- The approach based on memoization – combination of vectors and pure recursion.
Brief summary of the Fibonacci sequence
For a non-negative integer ![]() (including 0), the Fibonacci sequence is defined by
(including 0), the Fibonacci sequence is defined by
(1) ![]()
and
(2) ![]()
That is, the Fibonacci sequence can be computed by using a recursive formula (1), where the base cases are given by (2).
Computation of the Fibonacci Sequence by Using Recursion: Top-down Approach
Let us graphically analyze the Fibonacci recursion. The graphical representation of this recursion for ![]() is given in Fig. 1.
is given in Fig. 1.
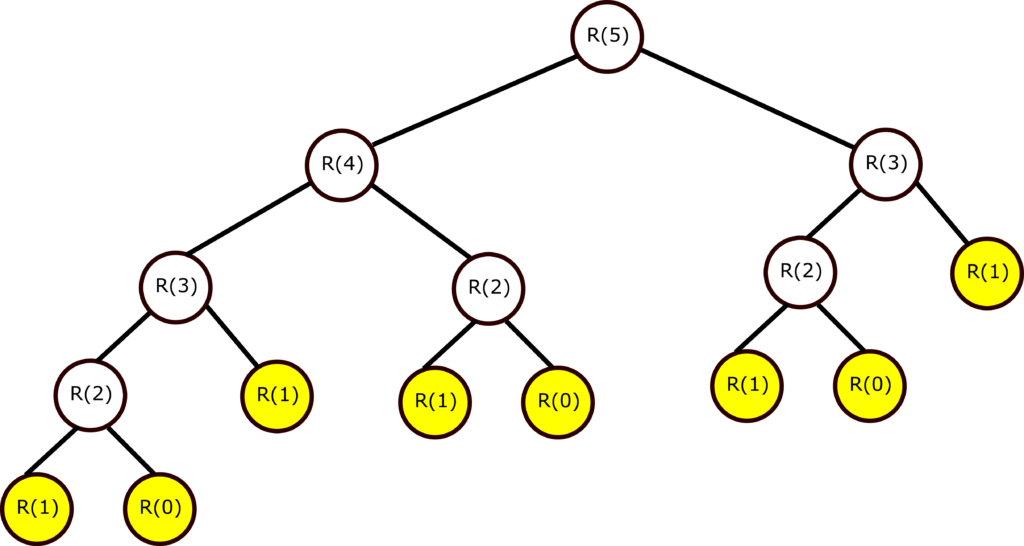
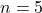 .
.We start from ![]() . We have to compute
. We have to compute
(3) ![]()
Then, we need to compute ![]() :
:
(4) ![]()
and ![]() :
:
(5) ![]()
We repeat this recursive procedure until we reach ![]() and
and ![]() . When we reach
. When we reach ![]() , we return 1, and when we reach
, we return 1, and when we reach ![]() , we return 0. In Fig. 1, the yellow circles represent the leaves of the tree at which we return values. These are the so-called base cases that are defined by (2).
, we return 0. In Fig. 1, the yellow circles represent the leaves of the tree at which we return values. These are the so-called base cases that are defined by (2).
The C++ code for computing the Fibonacci sequence by using the recursion is given below
#include<iostream>
using namespace std;
typedef unsigned long int uint;
// first approach - use pure recursion
uint fibonacciRecursion(uint n)
{
if (n<2)
{
return n;
}
return fibonacciRecursion(n-1)+fibonacciRecursion(n-2);
}
This code is not efficient (see the end of the post for the driver code that uses this function and that times it). There are more efficient approaches. The main reason for the code inefficiency is that we repeat computations of the same quantities many times recursively. For example, consider Fig. 1. The branch starting at node R(5) has three copies of R(2) and two copies of R(3). That is, we compute the same quantities many times and this increases the code inefficiency.
Computation of the Fibonacci Sequence by Using Vectors (Dynamic Arrays)
The second approach for computing the Fibonacci sequence does not rely upon recursion. Instead, it uses vectors (dynamic arrays), which are explained in our previous tutorial. This approach is more efficient than the second approach. The code is given below.
// second approach - use vectors
#include<vector>
#include<iostream>
using namespace std;
typedef unsigned long int uint;
uint fibonacciVector(uint n)
{
vector<uint> fibonacci;
fibonacci.push_back(0);
fibonacci.push_back(1);
for (uint i=2; i<=n; i++)
{
fibonacci.push_back(fibonacci[i-1]+fibonacci[i-2]);
}
return fibonacci.back();
}
However, this approach is still not the most efficient one. The next approach that combines vectors and recursion is more efficient.
Computation of the Fibonacci Sequence by Using Memoization: Combination of Recursion and Vectors
As explained previously, the recursive approach is not efficient since it computes many times copies of certain quantities. We can avoid this unnecessary computation by caching the values that are computed and checking in every iteration if a certain quantity was computed previously. This approach is called memoization (this is not a spelling error, this word is different from “memorization”).
#include<vector>
#include<iostream>
using namespace std;
typedef unsigned long int uint;
const int NOT_INCLUDED=-999;
const int DIM=10000;
vector<int> memoizationVector(DIM,NOT_INCLUDED);
uint fibonacciMemoization(uint n)
{
if (n<2)
{
return n;
}
if (memoizationVector[n]!=NOT_INCLUDED)
{
return memoizationVector[n];
}
else
{
unsigned int fibonacciVector_n=fibonacciMemoization(n-1)+fibonacciMemoization(n-2);
memoizationVector[n]=fibonacciVector_n;
return fibonacciVector_n;
}
}
First, we declare a vector “memoizationVector” in the global space that will track if a certain quantity was computed previously and that will store the previously computed entries. That is, if ![]() has been computed, then memoizationVector[i]=
has been computed, then memoizationVector[i]=![]() , and we will simply return the previously computed value, instead of recomputing it. If the quantity was not computed previously, then we compute this quantity and store it inside of memoizationVector. The integer that indicates that a quantity was not computed previously is “NOT_INCLUDED=-999”. When declaring the vector memoizationVector, we set all of its entries to -999, to ensure proper initialization.
, and we will simply return the previously computed value, instead of recomputing it. If the quantity was not computed previously, then we compute this quantity and store it inside of memoizationVector. The integer that indicates that a quantity was not computed previously is “NOT_INCLUDED=-999”. When declaring the vector memoizationVector, we set all of its entries to -999, to ensure proper initialization.
Driver code for three functions and timing
The driver code for testing these three approaches is given below. We also time the execution of all three functions.
// this code implements three approaches for computing the Fibonacci sequence
// Author: Aleksandar Haber
// date: December 2022
#include<iostream>
#include<vector>
// this library is necessary for timing the code
#include <chrono>
using namespace std;
typedef unsigned long int uint;
// first approach - use pure recursion
uint fibonacciRecursion(uint n)
{
if (n<2)
{
return n;
}
return fibonacciRecursion(n-1)+fibonacciRecursion(n-2);
}
// second approach - use vectors
uint fibonacciVector(uint n)
{
vector<uint> fibonacci;
fibonacci.push_back(0);
fibonacci.push_back(1);
for (uint i=2; i<=n; i++)
{
fibonacci.push_back(fibonacci[i-1]+fibonacci[i-2]);
}
return fibonacci.back();
}
// third approach - use vectors, recursion, and memoization to optimize the code
const int NOT_INCLUDED=-999;
const int DIM=10000;
vector<int> memoizationVector(DIM,NOT_INCLUDED);
uint fibonacciMemoization(uint n)
{
if (n<2)
{
return n;
}
if (memoizationVector[n]!=NOT_INCLUDED)
{
return memoizationVector[n];
}
else
{
unsigned int fibonacciVector_n=fibonacciMemoization(n-1)+fibonacciMemoization(n-2);
memoizationVector[n]=fibonacciVector_n;
return fibonacciVector_n;
}
}
int main()
{
uint n=30;
clock_t startTime, endTime;
// solution computed by using fibonacciRecursion(n)
uint fibonacciRecursionResult;
// solution computed by using fibonacciVector(n)
uint fibonacciVectorResult;
// solution computed by fibonacciMemoization(n)
uint fibonacciMemoizationResult;
// declare everything here in order not to include time for reserving the memory space for variables
auto start = chrono::steady_clock::now();
auto end = chrono::steady_clock::now();
auto fibonacciRecursionResultTime=chrono::duration_cast<chrono::nanoseconds> (end-start).count();
auto fibonacciVectorResultTime=chrono::duration_cast<chrono::nanoseconds> (end-start).count();
auto fibonacciMemoizationResultTime=chrono::duration_cast<chrono::nanoseconds> (end-start).count();
// compute the solution by using the fibonacciRecursion(n)
start = chrono::steady_clock::now();
fibonacciRecursionResult = fibonacciRecursion(n);
end = chrono::steady_clock::now();
fibonacciRecursionResultTime=chrono::duration_cast<chrono::nanoseconds> (end-start).count();
// compute the solution by using the fibonacciVector(n)
start = chrono::steady_clock::now();
fibonacciVectorResult = fibonacciVector(n);
end = chrono::steady_clock::now();
fibonacciVectorResultTime=chrono::duration_cast<chrono::nanoseconds> (end-start).count();
// compute the solution by using the fibonacciMemoization(n)
start = chrono::steady_clock::now();
fibonacciMemoizationResult = fibonacciMemoization(n);
end = chrono::steady_clock::now();
fibonacciMemoizationResultTime=chrono::duration_cast<chrono::nanoseconds> (end-start).count();
cout<<"Fibonacci sequence of n="<<n<< " by using recursion is: "<<fibonacciRecursionResult<< ". Time: " << fibonacciRecursionResultTime << " nanoseconds"<<endl;
cout<<"Fibonacci sequence of n="<<n<< " by using vectors (STL) is: "<<fibonacciVectorResult<< ". Time: " << fibonacciVectorResultTime << " nanoseconds"<<endl;
cout<<"Fibonacci sequence of n="<<n<< " by using memoization is: "<<fibonacciMemoizationResult<< ". Time: " << fibonacciMemoizationResultTime << " nanoseconds"<<endl;
/* cout<<"Memoization vector entries are: "<<endl;
vector<int>::iterator printIterator;
for(printIterator=memoizationVector.begin();printIterator!=memoizationVector.begin();printIterator++)
{
cout<<*printIterator<<endl;
}
*/
}
The timing results are given below
- The Fibonacci sequence of n=30 by using recursion is: 832040. Time: 7337800 nanoseconds.
- The Fibonacci sequence of n=30 by using vectors (STL) is: 832040. Time: 30400 nanoseconds.
- The Fibonacci sequence of n=30 by using memoization is: 832040. Time: 900 nanoseconds.