In this tutorial, you will learn how to solve optimization problems in C/C++ by using the NLopt library. The YouTube tutorial accompanying this page is given below.
NLopt is a free and open-source library for nonlinear optimization in C/C++. It is very simple to use and is relatively well documented. It supports both local and global optimization methods. It also contains algorithms that are derivative-free.
This tutorial assumes that you have already installed the NLopt library. The installation procedure can be found here. However, our experience shows that you should also consult this page in order to complete the installation.
Test Case and NLopt C code
To explain how to use the NLopt library, we consider the following optimization problem
(1) 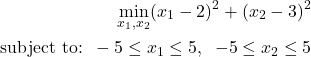
Obviously, this is a convex optimization problem with the global minimum located at ![]() . Let us now explain how to solve this problem by using the NLopt library.
. Let us now explain how to solve this problem by using the NLopt library.
The first step is to import the necessary libraries. We import
#include <math.h>
#include <nlopt.h>
#include <stdio.h>
The first library is the math library. The second file is the NLopt header file, and the third library is the standard C library.
The next step is to specify the cost function. The following function specifies the cost function
double costFunction(unsigned n, const double *x, double *grad, void *data)
{
// define the gradient vector
if(grad)
{
grad[0]=2*(x[0]-2);
grad[1]=2*(x[1]-3);
}
// return value is the value of the cost function
return ( (x[0]-2)*(x[0]-2)+ (x[1]-3)*(x[1]-3) );
}
The input arguments of this function are
- “unsigned n” – dimension of the optimization problem. In our case n will be equal to 2
- “const double *x” – this is a pointer to an array of optimization variables. In our case since we have two optimization variables, the array will contain two entries x[0] and x[1]
- “double *grad” – pointer to an array of objective function gradients. Our cost function will populate this array in every optimization step.
- “void *data” – pointer to a data structure that can be used to pass additional parameters to our objective function (for example constants). We do not use this pointer in the tutorial.
This function returns as output the value of the cost function at the current optimization array (vector) x. In the function body, we populate the gradient vector and compute/return the cost function value at x.
The next step is to define our main function and to define additional optimization variables in this function. The main function is given below.
int main()
{
double lb[2] = { -5.0, -5.0 }; //lower bounds
double ub[2] = {5.0 , 5.0 }; //upper bounds
// create the optimization problem
// opaque pointer type
nlopt_opt opt;
opt = nlopt_create(NLOPT_LD_MMA, 2);
nlopt_set_lower_bounds(opt,lb);
nlopt_set_upper_bounds(opt,ub);
nlopt_set_min_objective(opt, costFunction,NULL);
nlopt_set_xtol_rel(opt, 1e-4);
// initial guess
double x[2]={0.0,0.0};
double minf;
nlopt_result res=nlopt_optimize(opt, x,&minf);
if (res < 0) {
printf("nlopt failed!\n");
}
else {
printf("found minimum at f(%g,%g) = %0.10g\n", x[0], x[1], minf);
}
}
Next, we explain the above-summarized code. First, we define the lower and upper bounds as two arrays:
double lb[2] = { -5.0, -5.0 }; //lower bounds
double ub[2] = {5.0 , 5.0 }; //upper bounds
Next, we create the optimization problem. The library NLopt is centered around the object of type nlopt_opt. This is an opaque pointer type. We pass this pointer to subsequent functions to set the optimization parameters, such as, algorithm, dimensions, constraints, objective function, stopping tolerances, etc. We create this object by using the following code lines
nlopt_opt opt;
opt = nlopt_create(NLOPT_LD_MMA, 2);
The function “nlopt_create” returns a newly allocated “nlopt_opt” object and sets is parameters:
- “NLOPT_LD_MMA” – is the name of the optimization algorithm. NLOPT is a standard string, L-means that the optimization algorithm is local, D – means that the algorithm is based on derivatives, and MMA is the name of the algorithm: “Method of Moving Asymptotes”:
Krister Svanberg, “A class of globally convergent optimization methods based on conservative convex separable approximations,” SIAM J. Optim. 12 (2), p. 555-573 (2002). - 2 – is the dimension of the problem (number of optimization parameters), in our case n=2.
We set the lower and upper bounds by using the following two functions
nlopt_set_lower_bounds(opt,lb);
nlopt_set_upper_bounds(opt,ub);
Note that we pass to these functions the previously created “opt” object and the array pointers pointing to arrays storing the lower and upper bounds. Next, we add the previously defined objective function to our problem
nlopt_set_min_objective(opt, costFunction,NULL);
The first input argument is our “opt” object of type “nlopt_opt”, the second input argument is our previously defined cost function, and the third argument is “NULL”. This third argument is actually of the type “void* f_data” and it is the same pointer used in the definition of the objective function. The general form the function for adding the objective function is:
nlopt_result nlopt_set_min_objective(nlopt_opt opt, nlopt_func f, void* f_data);
We use the following code lines to define an initial guess for optimization, define the final value of the objective function, and to solve the optimization problem:
nlopt_set_xtol_rel(opt, 1e-4);
// initial guess
double x[2]={0.0,0.0};
double minf;
nlopt_result res=nlopt_optimize(opt, x,&minf);
Here, the initial guess of the solution is the vector of zeros. The function “nlopt_optimize” solves the optimization problem, and has the following general form
nlopt_result nlopt_optimize(nlopt_opt opt, double *x, double *opt_f);
The first input argument is the object of the type “nlopt_opt”, the second input argument is a pointer to an array storing initial guess. Note that after the optimization is completed, this array will also store the solution. The third argument stores the value of the objective function. If the optimization process is successful the function will return a positive value, otherwise it will return a negative value. For more information on return flags stored in “res” see this page.
Finally, we print the results by using the following code lines
if (res < 0) {
printf("nlopt failed!\n");
}
else {
printf("found minimum at f(%g,%g) = %0.10g\n", x[0], x[1], minf);
}
The complete code is given below.
#include <math.h>
#include <nlopt.h>
#include <stdio.h>
double costFunction(unsigned n, const double *x, double *grad, void *data)
{
// define the gradient vector
if(grad)
{
grad[0]=2*(x[0]-2);
grad[1]=2*(x[1]-3);
}
// return value is the value of the cost function
return ( (x[0]-2)*(x[0]-2)+ (x[1]-3)*(x[1]-3) );
}
int main()
{
double lb[2] = { -5.0, -5.0 }; //lower bounds
double ub[2] = {5.0 , 5.0 }; //upper bounds
// create the optimization problem
// opaque pointer type
nlopt_opt opt;
opt = nlopt_create(NLOPT_LD_MMA, 2);
nlopt_set_lower_bounds(opt,lb);
nlopt_set_upper_bounds(opt,ub);
nlopt_set_min_objective(opt, costFunction,NULL);
nlopt_set_xtol_rel(opt, 1e-4);
// initial guess
double x[2]={0.0,0.0};
double minf;
nlopt_result res=nlopt_optimize(opt, x,&minf);
if (res < 0) {
printf("nlopt failed!\n");
}
else {
printf("found minimum at f(%g,%g) = %0.10g\n", x[0], x[1], minf);
}
}
Save that code in the file called “optimizationTest.c”. Under the assumption that you are in the Linux/Unix environment, you can compile this file by typing in terminal
cc optimizationTest.c -lnlopt -lm -o optimizationTestFinal
This code line will compile the code and it will produce the output file “optimizationTestFinal”. You can execute that file by typing in the command line
./optimizationTestFinal
The result should look like this:
found minimum at f(2,3) = 3.790613212e-16