Policy Iteration Algorithm in Python and Tests with Frozen Lake OpenAI Gym Environment- Reinforcement Learning Tutorial – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In our previous tutorial, which can be found here, we introduced the iterative policy evaluation algorithm for computing the state-value function. We also explained how to implement this algorithm in Python, and we tested the algorithm on the Frozen Lake Open AI Gym environment introduced in this post. The GitHub page with the codes developed in this tutorial is given here.

In this tutorial, we introduce a policy iteration algorithm. We explain how to implement this algorithm in Python and we explain how to solve the Frozen Lake problem by using this algorithm. Before reading this post, you should get yourself familiar with the following topics (links provided below):

Motivation and Final Solution

Our goal is to solve the Frozen Lake problem. The Frozen Lake problem and its environment are explained in our previous post. This environment is illustrated in the figure below.

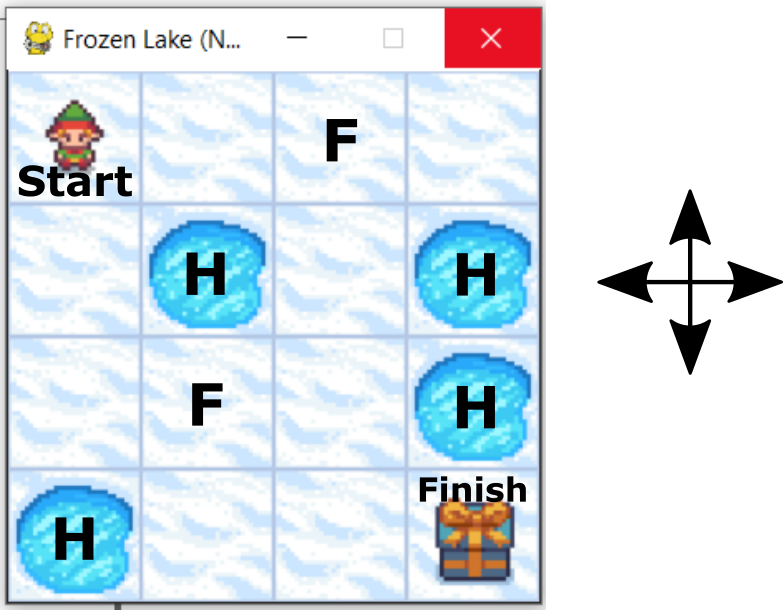
The goal is to reach “Finish” field starting from “Start” field. We can only perform the actions “UP”, “DOWN”, “LEFT”, and “RIGHT”. We have two types of fields: frozen field, denoted by “F”, and the hole field denoted by “H”. We can safely step on the frozen field. However, if we step on hole fields, we unsuccessfully end the game. The goal is to design a series of actions (“UP”,”DOWN”,”LEFT”, and “RIGHT”), such that we reach the finish the finish state by maximizing a reward function. In this post, we teach you how to solve this problem. The solution is shown in the figure below.

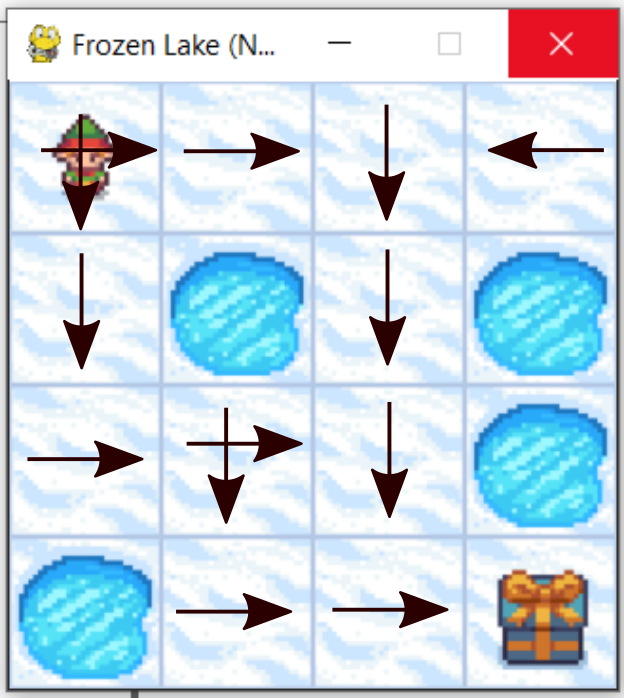
Figure 2: Solution of the Frozen Lake problem.

This solution is explained below.

Explanation of the Policy Iteration Algorithm

First, we need to introduce and explain the implementation of the policy iteration algorithm. The state value function is introduced and interpreted in our previous tutorial. The state value function has the following form, expressed by its Bellman equation:

(1) $\begin{align*}v_{\pi}(s) & =E_{\pi}[G_{t}|S_{t}=s] \\v_{\pi}(s) & = \sum_{a} \pi(a|s) \sum_{s'}\sum_{r}p(s',r|s,a)[r+\gamma v_{\pi}(s')]\end{align*}$

where

$E_{\pi}[\cdot]$ is the mathematical expectation assuming that the agent follows the policy $\pi$
$v_{\pi}(s)$ is the state value function
$t$ is the current time step
$s$ is the current state
$G_{t}$ is the return (weighted sum of rewards)
$a$ is the action
$r$ is the reward
$s'$ is one of the possible states at the next time instant $t+1$
$\pi(a|s)$ is the policy (probability of selecting a certain action $a$ at the state $s$ )
$p(s',r|s,a)$ is the dynamics (probability of reaching the state $s'$ at the next time instant $t+1$ and obtaining the reward $r$ if the agent is in the state $s$ at the time instant $t$ , and if the agent applied the action $a$ at the time instant $t$ )

In addition to the state value function (1), for the policy iteration algorithm, we also need an action-value function. The action value function is defined as follows:

(2) $\begin{align*}q_{\pi}(s) & =E_{\pi}[G_{t}|S_{t}=s,A_{t}=a] \end{align*}$

Here you should immediately notice the main difference between (1) and (2). The action value function is defined under the assumption that the agent takes an action $a$ in the state $s$ at the current time instant $t$ . That is, the action value function is the expected return from the state $s$ under the assumption that the agent took the action $a$ . On the other hand, the state value function (1) does not assume that the particular action $a$ is taken at the state $s$ . That is, the state value function is defined by assuming that a particular action is not being taken.

The Bellman equation for the action value function is

(3) $\begin{align*}q_{\pi}(s)= \sum_{s'}\sum_{r}p(s',r|s,a)[r+\gamma v_{\pi}(s')]\end{align*}$

In the sequel let us design an algorithm that will try to find an optimal policy that will maximize the state value function. That is, we want to find actions that will maximize the expected return from the state $s$ . The Bellman optimality equation for the state value function can provide us with a good direction for solving this problem. Before we introduce the Bellman optimality equation for the state value function, we introduce the optimal state-value function:

(4) $\begin{align*}v_{*}(s)=\max_{\pi} v_{\pi}(s)\end{align*}$

and we introduce the optimal action-value function

(5) $\begin{align*}q_{*}(s,a)=\max_{\pi} q_{\pi}(s,a)\end{align*}$

Let the optimal policy that solves (4) and (5), be denoted by $\pi_{*}$ . Let us for a moment stop and analyze (4) and (5). The optimal state-value and action-value functions are obtained by finding the optimal policy $\pi_{*}$ that will produce the highest value of the expected return under the two scenarios used to define the state-value and action-value functions.

Next, we have that

(6) $\begin{align*}v_{*}(s)=\max_{a} q_{\pi_{*}} (s,a)\end{align*}$

From the last equation, and by using a similar strategy to the strategy used to derive (3), we obtain the Bellman optimality equation for the state value function:

(7) $\begin{align*}v_{*}(s)=\max_{a} \sum_{s'}\sum_{r}p(s',r|s,a)[r+\gamma v_{*}(s')]\end{align*}$

The equations (3), (6), and (7) can give us a clue on how to determine an optimal policy. Let us say that we start our search for an optimal policy, with a certain policy $\pi_{0}(s)$ that is suboptimal or even completely random. That is, we can randomly select this policy. In the notation, $\pi_{0}(s)$ , the subscript $0$ denotes an iteration of finding the optimal policy. This policy is defined for every state $s$ . For such a fixed and known policy, we can compute the state value function $v_{\pi_{0}}(s)$ for every state $s$ by using the iterative policy evaluation algorithm, which is explained in our previous post. Then, once we have $v_{\pi_{0}}(s)$ , we can determine a new improved policy by maximizing with respect to actions $a$ the action value function at that state. That is,

(8) $\begin{align*}\text{action to take in state s} & =\underset{a}{\text{argmax}} \;\;\; q_{\pi_{0}}(s,a) \end{align*}$

From (3) and (8), we have

(9) $\begin{align*}\text{action to take in state s} & = \underset{a}{\text{argmax}} \;\;\; \underbrace{\sum_{s'}\sum_{r}p(s',r|s,a)[r+\gamma v_{\pi_{0}}(s')]}_{q_{\pi_{0}}(s,a)}\end{align*}$

The solution of (9) actually defines an improved policy $\pi_{1}$ . Note here that if there is only a single solution to this problem, then the computed policy $\pi_{1}$ is completely deterministic. That is, if the solution is denoted by $\hat{a}$ , then $\pi_{1}(\hat{a}|s)=1$ . That is, we always select $\hat{a}$ . On the other hand, if there are multiple solutions that produce the same maximal value, then we can assign an equal probability to each of these solutions, and in this way obtain the policy $\pi_{1}$ . In practice, we can solve the problem (9), by evaluating the action value functions

(10) $\begin{align*} q_{\pi_{0}}(s,a) =\sum_{s'}\sum_{r}p(s',r|s,a)[r+\gamma v_{\pi_{0}}(s')] \end{align*}$

for all possible actions $a$ starting from the fixed state $s$ . Then, we can choose the action that produces the maximum action-value function, and this action (or actions if there are multiple actions that produce the same maximum) define the policy $\pi_{1}$ .

Next, for the newly computed policy $\pi_{1}$ , we compute the state value function $v_{\pi_{1}}(s)$ by using the iterative policy evaluation algorithm. Then, we compute the new actions and policy by solving:

(11) $\begin{align*}\text{action to take in state s} & = \underbrace{\underset{a}{\text{argmax}} \;\;\; \sum_{s'}\sum_{r}p(s',r|s,a)[r+\gamma v_{\pi_{1}}(s')]}_{ q_{\pi_{1}}(s,a)}\end{align*}$

The solution of (11) defines a new policy $\pi_{2}$ . These two steps are repeated iteratively until convergence. This is the main idea of the policy iteration algorithm that is summarized below.

POLICY ITERATION ALGORITHM:

Perform these two steps iteratively until convergence of the computed policy $\pi_{k}$

Policy evaluation: For the policy $\pi_{k}$ compute the state-value function $v_{\pi_{k}}(s)$ by using the iterative policy evaluation algorithm for every state s.
Policy improvement: For the computed state-value function $v_{\pi_{k}}(s)$ , for every state s, compute the action to be taken in state s by solving
(12) $\begin{align*}& \text{action to take in state s} = \underset{a}{\text{argmax}} \;\;\; q_{\pi_{k}}(s,a) \\ & q_{\pi_{k}}(s,a)=\sum_{s'}\sum_{r}p(s',r|s,a)[r+\gamma v_{\pi_{k}}(s')] \end{align*}$

The solution of (12) defines an improved policy $\pi_{k+1}$ in the state $s$ . After this step is finished increment $k$ and go to step 1.

As mentioned previously this algorithm can be initialized with a complete random policy or with a policy obtained on the basis of some a priori knowledge about the environment.

Python Implementation

The GitHub page with the codes developed in this tutorial is given here. To test the policy iteration algorithm, we use the Frozen Lake environment explained in this tutorial. Here, we only provide a photo of the Frozen Lake environment, for more details see the tutorial. The Frozen Lake environment is shown in Fig. 3. below.

The states $s_{1},s_{2},\ldots, s_{16}$ together with the corresponding state value functions $v_{\pi}(s_{1}),v_{\pi}(s_{2}),\ldots , v_{\pi}(s_{16})$ are shown in Fig. 4. below.

Figure 4: States and state-value functions.

The first step is to define two functions. The first function will be used to implement the step 1 of the policy iteration algorithm. That is, this function will evaluate the policy or better to say, this function will compute the state-value function for a given policy. This function is actually developed in our previous tutorial, and here for brevity, we will not explain this function again. We will only briefly explain its inputs and outputs, and the general purpose. The function is given below.

##################
# this function computes the state value function by using the iterative policy evaluation algorithm
##################
# inputs: 
##################
# env - environment 
# valueFunctionVector - initial state value function vector
# policy - policy to be evaluated - this is a matrix with the dimensions (number of states)x(number of actions)
#        - p,q entry of this matrix is the probability of selection action q in state p
# discountRate - discount rate 
# maxNumberOfIterations - max number of iterations of the iterative policy evaluation algorithm
# convergenceTolerance - convergence tolerance of the iterative policy evaluation algorithm
##################
# outputs:
##################
# valueFunctionVector - final value of the state value function vector 

##################
def evaluatePolicy(env,valueFunctionVector,policy,discountRate,maxNumberOfIterations,convergenceTolerance):
    import numpy as np
    convergenceTrack=[]
    for iterations in range(maxNumberOfIterations):
        convergenceTrack.append(np.linalg.norm(valueFunctionVector,2))
        valueFunctionVectorNextIteration=np.zeros(env.observation_space.n)
        for state in env.P:
            outerSum=0
            for action in env.P[state]:
                innerSum=0
                for probability, nextState, reward, isTerminalState in env.P[state][action]:
                    #print(probability, nextState, reward, isTerminalState)
                    innerSum=innerSum+ probability*(reward+discountRate*valueFunctionVector[nextState])
                outerSum=outerSum+policy[state,action]*innerSum
            valueFunctionVectorNextIteration[state]=outerSum
        if(np.max(np.abs(valueFunctionVectorNextIteration-valueFunctionVector))<convergenceTolerance):
            valueFunctionVector=valueFunctionVectorNextIteration
            print('Iterative policy evaluation algorithm converged!')
            break
        valueFunctionVector=valueFunctionVectorNextIteration       
    return valueFunctionVector

The first argument of this function, called “env” is the OpenAI Gym Frozen Lake environment. The second argument, called “valueFunctionVector” is the value function vector. It represents an initial value of the state-value function vector. This vector is iteratively updated by this function, and its value is returned. For the Frozen Lake environment, this vector has the following form

(13) $\begin{align*}\text{valueFunctionVector}=\begin{bmatrix}v_{\pi}(s_{1}) \\ v_{\pi}(s_{2}) \\ \vdots \\ v_{\pi}(s_{16}) \end{bmatrix}\end{align*}$

The third argument, denoted by “policy” is a matrix defining the policy that needs to be evaluated. This matrix has this form

(14) $\begin{align*}\text{policy} = \begin{bmatrix} \pi(a_{1}|s_{1}) & \pi(a_{2}|s_{1}) & \pi(a_{3}|s_{1}) & \pi(a_{4}|s_{1}) \\ \pi(a_{1}|s_{2}) & \pi(a_{2}|s_{2}) & \pi(a_{3}|s_{2}) & \pi(a_{4}|s_{2}) \\ \vdots & \vdots & \vdots & \vdots \\ \pi(a_{1}|s_{16}) & \pi(a_{2}|s_{16}) & \pi(a_{3}|s_{16}) & \pi(a_{4}|s_{16}) \end{bmatrix}\end{align*}$

where $\pi(a_{p}|s_{q})$ is the probability of selecting the action $a_{p}$ in the state $q$ . The last three arguments are the discount rate $\gamma$ , max number of iterations, and convergence tolerance. These values are explained in the previous tutorial on the iterative policy evaluation.

The second function implements the step 2 of the policy iteration algorithm. That is, this function is used to improve the policy. The function is given below.

##################
# this function computes an improved policy 
##################
# inputs: 
# env - environment 
# valueFunctionVector - state value function vector that is previously computed
# numberActions - number of actions 
# numberStates - number of states 
# discountRate - discount rate

# outputs:
# improvedPolicy - improved policy
# qvaluesMatrix  - matrix containing computed action-value functions 
#                - (p,q) entry of this matrix is the action value function computed at the state p and for the action q
# Note: qvaluesMatrix is just used for double check - it is actually not used lated on    
    
    
##################

def improvePolicy(env,valueFunctionVector,numberActions,numberStates,discountRate):
    import numpy as np
    # this matrix will store the q-values (action value functions) for every state
    # this matrix is returned by the function 
    qvaluesMatrix=np.zeros((numberStates,numberActions))
    # this is the improved policy
    # this matrix is returned by the function
    improvedPolicy=np.zeros((numberStates,numberActions))
    
    for stateIndex in range(numberStates):
        # computes a row of the qvaluesMatrix[stateIndex,:] for fixed stateIndex, 
        # this loop iterates over the actions
        for actionIndex in range(numberActions):
            # computes the Bellman equation for the action value function
            for probability, nextState, reward, isTerminalState in env.P[stateIndex][actionIndex]:
                qvaluesMatrix[stateIndex,actionIndex]=qvaluesMatrix[stateIndex,actionIndex]+probability*(reward+discountRate*valueFunctionVector[nextState])
            
        # find the action indices that produce the highest values of action value functions
        bestActionIndex=np.where(qvaluesMatrix[stateIndex,:]==np.max(qvaluesMatrix[stateIndex,:]))

        # form the improved policy        
        improvedPolicy[stateIndex,bestActionIndex]=1/np.size(bestActionIndex)
    return improvedPolicy,qvaluesMatrix

Let us explain this function. The first argument is “env” which is previously explained. The second argument is “valueFunctionVector” that is the state-value function vector defined in (13). The remaining 3 input arguments are self-explanatory. This function returns the matrix called “improvedPolicy”, This matrix has the form shown in Eq.(14). The second output argument, called “qvaluesMatrix” has the following form

(15) $\begin{align*}\text{qvaluesMatrix}=\begin{bmatrix} q_{\pi}(s_{1},a_{1}) & q_{\pi}(s_{1},a_{2}) & q_{\pi}(s_{1},a_{3}) & q_{\pi}(s_{1}, a_{4}) \\ q_{\pi}(s_{2},a_{1}) & q_{\pi}(s_{2},a_{2}) & q_{\pi}(s_{2},a_{3}) & q_{\pi}(s_{2},a_{4}) \\ \vdots & \vdots & \vdots & \vdots \\ q_{\pi}(s_{16},a_{1}) & q_{\pi}(s_{16},a_{2}) & q_{\pi}(s_{16},a_{3}) & q_{\pi}(s_{16},a_{4}) \end{bmatrix}\end{align*}$

where $q_{\pi}(s_{p},a_{q})$ is the action-value function at the state $s_{p}$ and by applying the action $a_{q}$ . This matrix is only used to diagnose the accuracy of the algorithms. The code lines 29-35 are used to evaluate the equation for $q_{\pi_{k}}(s,a)$ and the code line 38 is used to solve the optimization problem (12). The code line 41 is used to compute every row of the matrix (14). That is to compute the probabilities. If for example, the value of “bestActionIndex” is 3 in the state $s_{1}$ , this means that we need to select $a_{4}$ in the state $s_{1}$ . In this case, the first row of the matrix is

(16) $\begin{align*}\text{qvaluesMatrix}[0,:]=\begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}\end{align*}$

On the other hand, it may happen that two values of $q(s,a)$ have the same value. For example, in the state $s_{1}$ , we might have bestActionIndex=[1,2]. That is, both actions $a_{2}$ and $a_{3}$ are optimal in the state $s_{1}$ . This means that

(17) $\begin{align*}\text{qvaluesMatrix}[0,:]=\begin{bmatrix} 0 & 0.5 & 0.5 & 0 \end{bmatrix}\end{align*}$

This means that we have a 50 $\%$ of a chance of selecting the actions $a_{2}$ and $a_{3}$ in the state $s_{1}$ . The driver code for these two functions is:

import gym
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from functions import evaluatePolicy
from functions import improvePolicy

# create the environment 
# this is a completely deterministic environment
env=gym.make('FrozenLake-v1', desc=None, map_name="4x4", is_slippery=False,render_mode="human")
# this is a completely stochastic environment - the algorithm will not work properly since the transition probabilities are equal -too much!
#env=gym.make("FrozenLake-v1", render_mode="human") 
env.reset()
# render the environment
# uncomment this if you want to render the environment
env.render()
#
env.close()

# investigate the environment
# observation space - states 
env.observation_space

env.action_space
# actions:
#0: LEFT
#1: DOWN
#2: RIGHT
#3: UP

##########################################################################
#           general parameters for the policy iteration
##########################################################################
# select the discount rate
discountRate=0.9
# number of states - determined by the Frozen Lake environment
stateNumber=16
# number of possible actions in every state - determined by the Frozen Lake environment
actionNumber=4
# maximal number of iterations of the policy iteration algorithm 
maxNumberOfIterationsOfPolicyIteration=1000

# select an initial policy
# initial policy starts with a completely random policy
# that is, in every state, there is an equal probability of choosing a particular action
initialPolicy=(1/actionNumber)*np.ones((stateNumber,actionNumber))
##########################################################################
#           parameters of the iterative policy evaluation algorithm
##########################################################################
# initialize the value function vector
valueFunctionVectorInitial=np.zeros(env.observation_space.n)
# maximum number of iterations of the iterative policy evaluation algorithm
maxNumberOfIterationsOfIterativePolicyEvaluation=1000
# convergence tolerance 
convergenceToleranceIterativePolicyEvaluation=10**(-6)
###########################################################################
###########################################################################

for iteration in range(maxNumberOfIterationsOfPolicyIteration):
    print("Iteration - {} - of policy iteration algorithm".format(iteration))
    if (iteration == 0):
        currentPolicy=initialPolicy
    valueFunctionVectorComputed =evaluatePolicy(env,valueFunctionVectorInitial,currentPolicy,discountRate,maxNumberOfIterationsOfIterativePolicyEvaluation,convergenceToleranceIterativePolicyEvaluation)
    improvedPolicy,qvaluesMatrix=improvePolicy(env,valueFunctionVectorComputed,actionNumber,stateNumber,discountRate)
    # if two policies are equal up to a certain "small" tolerance
    # then break the loop - our algorithm converged
    if np.allclose(currentPolicy,improvedPolicy):
        currentPolicy=improvedPolicy
        print("Policy iteration algorithm converged!")
        break
    currentPolicy=improvedPolicy

In the sequel, we only comment code lines that are not self-obvious. The code line 10 is used to is used to import the Frozen lake environment. Here it is very important to set the flag “is_slippery=False” . It is important to specify this flag to false since we want to ensure that the environment is deterministic. This means that the transition probabilities are 1. That is, $p(s'|s,a)=1$ . Otherwise, we will have a completely stochastic environment, and it is difficult to solve the reinforcement learning problem. On the code line 46, we specify the initial policy matrix (??). Every element of this matrix is 0.25. This means that every action in a fixed state is equally possible. The code lines 59 to 71 implement the policy iteration algorithm. We iteratively call evaluatePolicy and improvePolicy functions. The algorithm converges only after several iterations. The resulting policy is given below.

currentPolicy=
array([[0.  , 0.5 , 0.5 , 0.  ],
       [0.  , 0.  , 1.  , 0.  ],
       [0.  , 1.  , 0.  , 0.  ],
       [1.  , 0.  , 0.  , 0.  ],
       [0.  , 1.  , 0.  , 0.  ],
       [0.25, 0.25, 0.25, 0.25],
       [0.  , 1.  , 0.  , 0.  ],
       [0.25, 0.25, 0.25, 0.25],
       [0.  , 0.  , 1.  , 0.  ],
       [0.  , 0.5 , 0.5 , 0.  ],
       [0.  , 1.  , 0.  , 0.  ],
       [0.25, 0.25, 0.25, 0.25],
       [0.25, 0.25, 0.25, 0.25],
       [0.  , 0.  , 1.  , 0.  ],
       [0.  , 0.  , 1.  , 0.  ],
       [0.25, 0.25, 0.25, 0.25]])

Taking into account that actions are encoded as follows:

#0: LEFT
#1: DOWN
#2: RIGHT
#3: UP

These actions are the columns of the matrix “currentPolicy”. This solution can graphically represented in the figure shown below. Consider the first row of the matrix currentPolicy. The first row of this matrix represents the actions we should take in the initial state $s_{1}$ . When we are in the initial state 1 – we can either select down or right actions. That is, the probability of these actions is 0.5 each. Consider the second row. This row corresponds to the actions we should take in state $s_{2}$ . Since $1$ is located at the entry (2,3), we select with probability 1 action right. By using this interpretation method, we can select proper actions in every state. The result is shown in the figure below.

Motivation and Final Solution

Explanation of the Policy Iteration Algorithm

Python Implementation

admin

You might also like

Test 2

Convert State-Space Models into Transfer Functions with MATLAB Codes

Starting with FPGA coding – Learn how to turn on LEDs and implement simple digital logic