In this fluid mechanics tutorial, we explain how to derive an expression for the discharge velocity of a flow through a small opening (such as an orifice, outlet, nozzle, short pipe, or short tube) of a large tank. To derive this important expression, we use Bernoulli’s equation and the continuity equation (mass conservation principle). The derived expression is called as Torricelli’s law or Torricelli’s theorem. The YouTube video accompanying this webpage is given below.
Problem Formulation
Problem formulation: Consider a large tank filled with water and with a small opening (hole, outlet, short pipe, or nozzle) shown in the figure below. The water flows out of the tank through the small opening in the atmosphere.
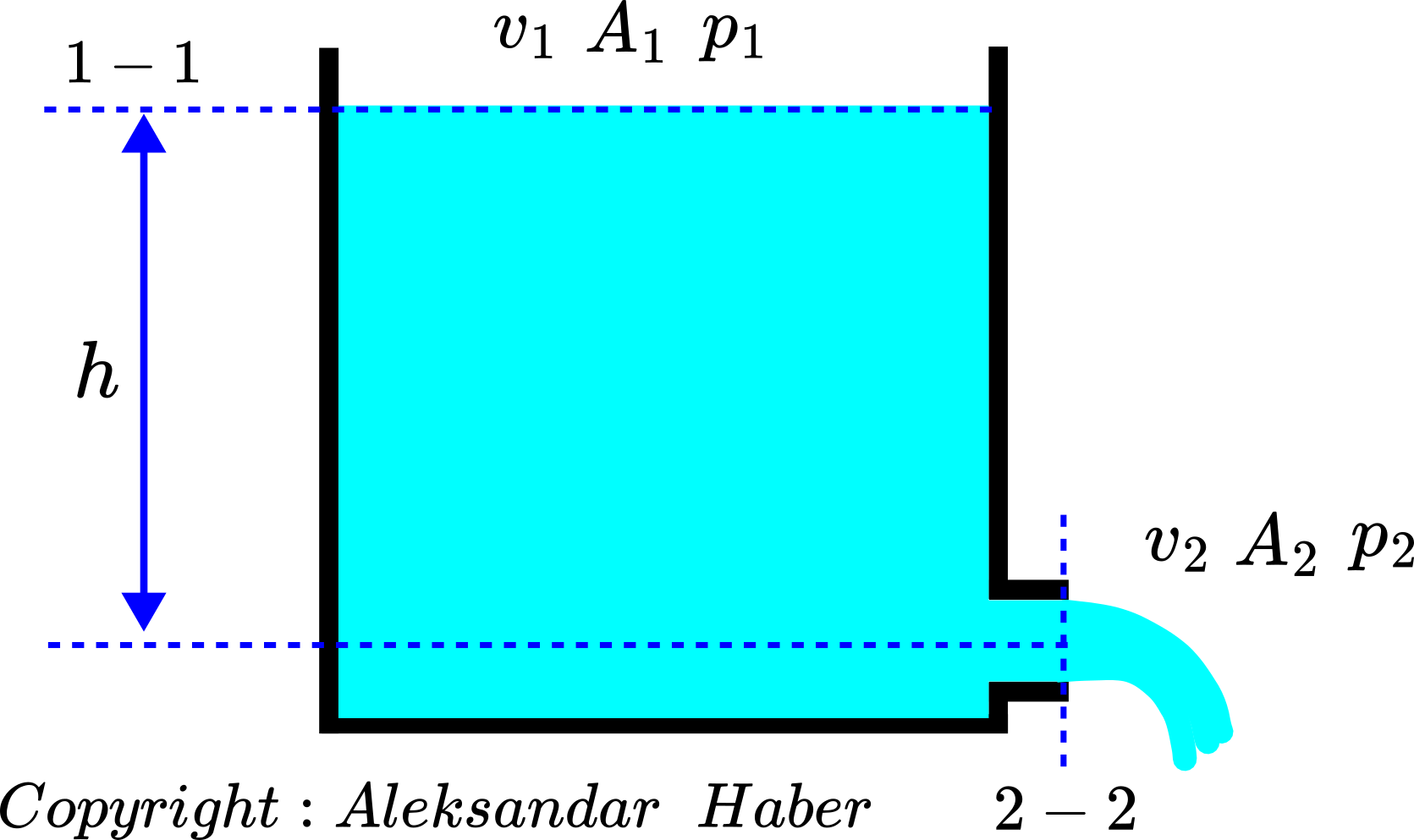
Consider the two cross-sections, denoted by 1-1 and 2-2. 1-1 denotes the cross-section of the tank and 2-2 denotes the cross-section of the hole. For simplicity, we assume that the cross-section areas of the tank and the hole are constant. The cross-section area of the tank is ![]() . The velocity of the top water level at the cross-section 1-1 is
. The velocity of the top water level at the cross-section 1-1 is ![]() . The pressure at the cross-section 1-1 is
. The pressure at the cross-section 1-1 is ![]() . The area of the cross section 2-2 is
. The area of the cross section 2-2 is ![]() . The velocity of the water through the cross-section 2-2 is
. The velocity of the water through the cross-section 2-2 is ![]() , and the pressure is
, and the pressure is ![]() . The height difference between the middle plane of the hole and the top water level is
. The height difference between the middle plane of the hole and the top water level is ![]() .
.
Assume that:
- The flow is steady, incompressible, and frictionless.
- There is no fluid-mechanical energy inserted in the system (no shaft work) and there is no heat transfer.
- Pressure
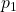 is equal to the pressure
is equal to the pressure 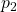 and equal to the atmospheric pressure.
and equal to the atmospheric pressure.
Under the assumption that ![]() ,
, ![]() ,
, ![]() , and gravitational acceleration constant
, and gravitational acceleration constant ![]() are given, calculate the discharge velocity
are given, calculate the discharge velocity ![]() .
.
Solution
We solve the problem by using Bernoulli’s equation and the continuity equation. The assumptions stated in the problem formulation satisfy the main assumptions necessary to apply Bernoulli’s equation. Consider the figure shown below.
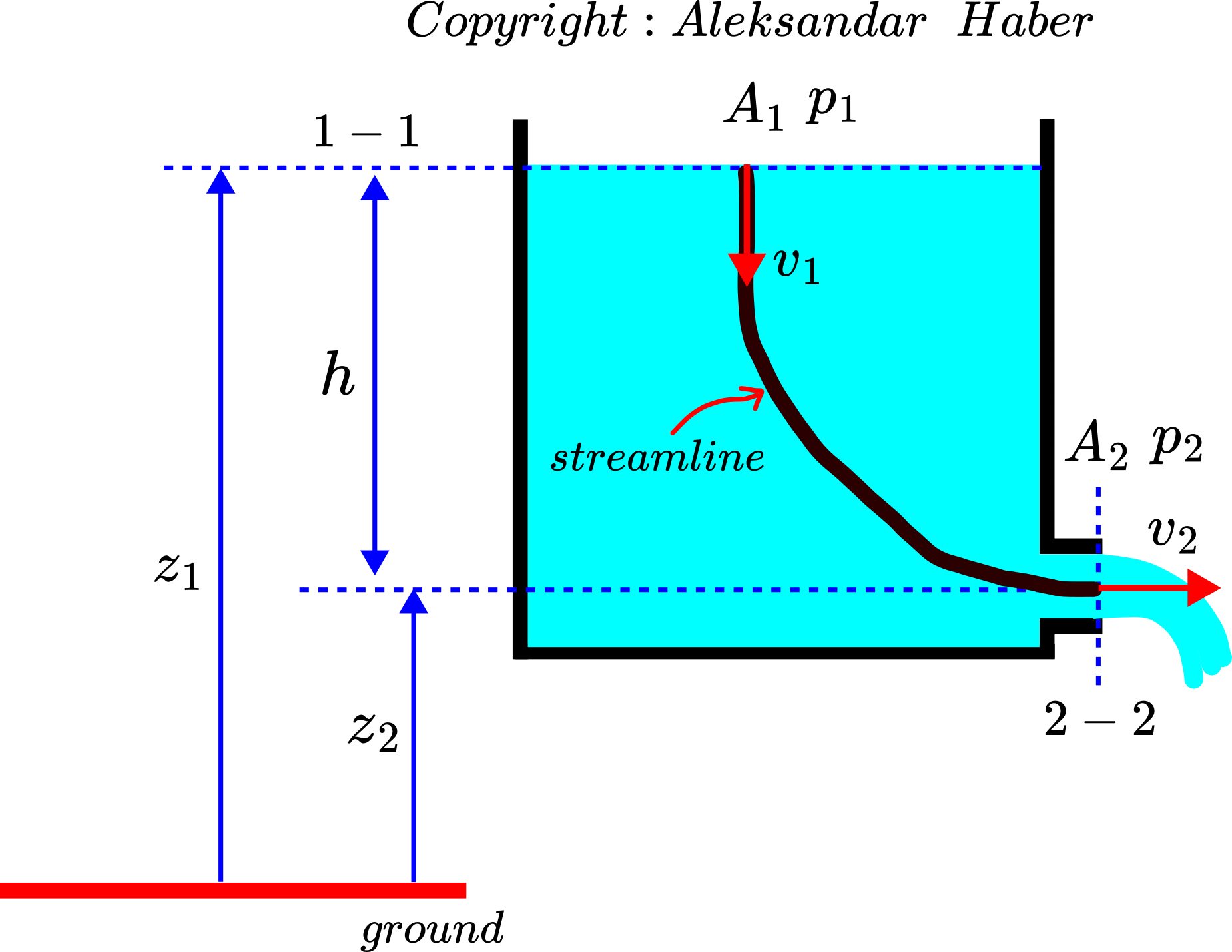
To apply Bernoulli’s equation, we first need to identify a streamline. The streamline is represented by a black line in the figure above. Then, Bernoulli’s equation has the following form
(1) ![]()
where ![]() is the fluid density. Since
is the fluid density. Since ![]() , where
, where ![]() is the atmospheric pressure, from (1), we have
is the atmospheric pressure, from (1), we have
(2) ![]()
From the last equation, we need to eliminate ![]() . We can eliminate
. We can eliminate ![]() by using the continuity equation
by using the continuity equation
(3) ![]()
This equation means that the flow is continuous. From the last equation, we obtain
(4) ![]()
By substituting (4) in (2), we obtain
(5) ![]()
From the last equation (5), we obtain
(6) 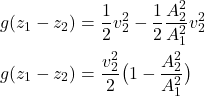
Since ![]() , from the last equation, we have
, from the last equation, we have
(7) ![]()
From the last equation, we have
(8) 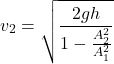
This is the final expression for the velocity discharge from the tank.
If ![]() is much larger than
is much larger than ![]() , then we have
, then we have
(9) ![]()
and the last expression becomes
(10) ![]()
The last equation represents the mathematical formulation of Torricelli’s law or Torricelli’s theorem.
Here, it should be noted that the discharge velocity equation (10) is derived under the ideal assumptions stated in the problem formulation. In practice, the flow through the opening is not one-dimensional and is not uniform. Also, the friction, turbulence, and viscosity effects produce a non-uniform velocity profile across the opening. To take all these effects into account, we can adjust the equation (10) as follows
(11) ![]()
where ![]() is the average velocity of the fluid flowing through the outlet and
is the average velocity of the fluid flowing through the outlet and ![]() is the discharge coefficient that usually varies from 0.6 to 1.0 and is a function of dimensionless flow conditions and opening shape (nozzle, orifice, or simple hole). For a round hole and low-viscosity fluids (such as water), the discharge coefficient is around 0.65. For a round tube or a hose, the discharge coefficient is around 0.9.
is the discharge coefficient that usually varies from 0.6 to 1.0 and is a function of dimensionless flow conditions and opening shape (nozzle, orifice, or simple hole). For a round hole and low-viscosity fluids (such as water), the discharge coefficient is around 0.65. For a round tube or a hose, the discharge coefficient is around 0.9.