In this post, we explain how to solve an inverse kinematics problem of a robot with two degrees of freedom. In this relatively simple case, it is possible to solve the inverse kinematics problem analytically (that is, to compute the closed-form solution). The purpose of this example is to introduce the inverse kinematics problem. The YouTube video accompanying this post can be found here
Consider a manipulator with two rotational degrees of freedom ![]() and
and ![]() shown in the figure below.
shown in the figure below.
The inverse kinematics problem can be formulated as follows:
Given the coordinates x and y of the end-effector point C (world coordinates), compute the angles ![]() and
and ![]() (local joint coordinates).
(local joint coordinates).
In the statement of the inverse kinematics problem, it is assumed that the lengths of the robotic segments ![]() and
and ![]() are given.
are given.
From Figure 1, we have
(1) ![]()
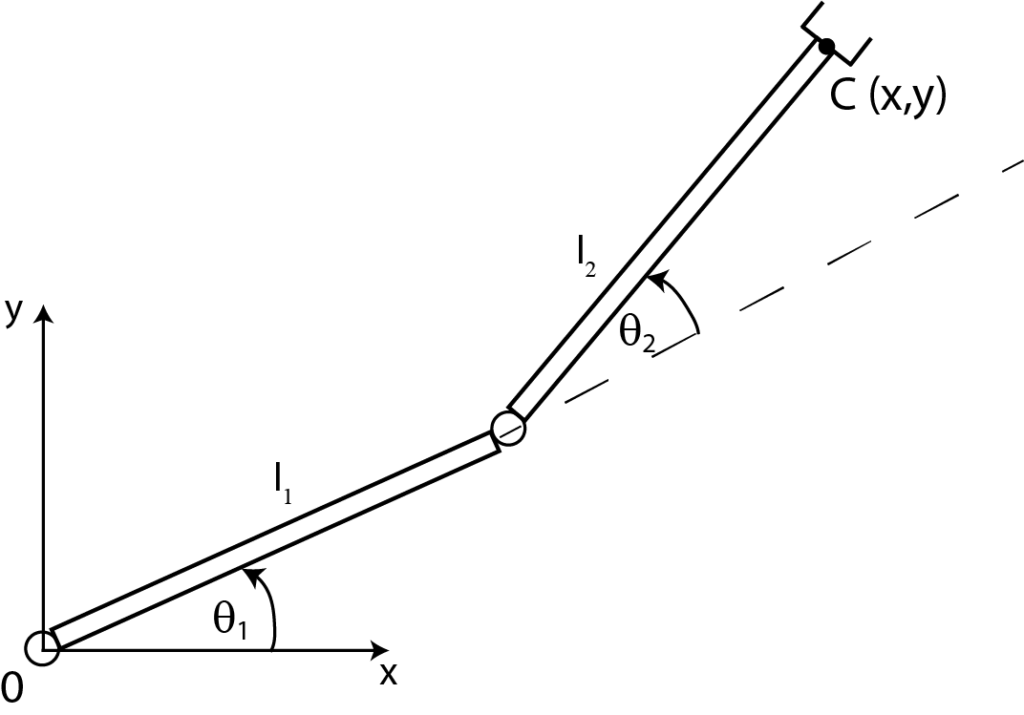
By squaring the last two equations and adding them together, we obtain
(2) ![]()
Next, we use the following trigonometric formula
(3) ![]()
By using this formula with ![]() and
and ![]() , from (2), we have
, from (2), we have
(4) 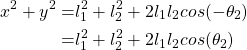
where we have used the identity ![]() (cosine function is an even function). From the last equation, we have
(cosine function is an even function). From the last equation, we have
(5) ![]()
The last equation enables us to compute the angle ![]() as a function of
as a function of ![]() and
and ![]() .
.
Here, an important observation should be made. Let us assume that the right-hand of the equation (5) is equal to ![]() . To compute
. To compute ![]() , we need to solve this equation
, we need to solve this equation
(6) ![]()
This equation has an infinite number of solutions, however, there are only two solutions that are physically unique and physically realistic, these solutions are
(7) ![]()
The figure below illustrates a similar scenario. We can observe that there are two possibilities for reaching point C (red and black manipulator positions).
This is a common situation when solving the inverse kinematics problem.
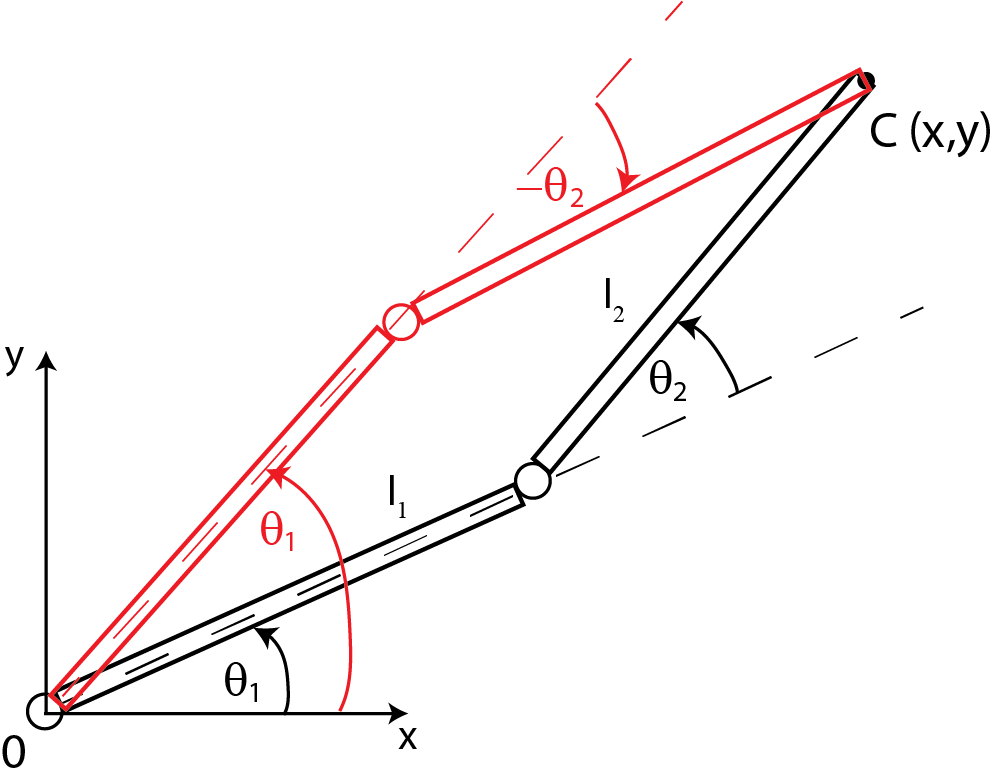
We will determine the angle ![]() by analyzing the figure shown below.
by analyzing the figure shown below.
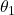 .
.From the figure 3, we have
(8) ![]()
where ![]() and
and ![]() are angles shown in the figure below. We will find
are angles shown in the figure below. We will find ![]() by using the tan() function. From (8), we have
by using the tan() function. From (8), we have
(9) ![]()
Next, we will use the following formula
(10) ![]()
From Fig. 3, we have
(11) ![]()
on the other hand, from triangles OMC and CMS, we have
(12) ![]()
Here, it should be noted that ![]() is only a function of
is only a function of ![]() , so once
, so once ![]() is determined from (5), we can find
is determined from (5), we can find ![]() from (12).
from (12).
By substituting (11) and (12) in (10), we obtain the final result for ![]()
(13) ![]()