In this post, we explain how to implement the perceptron neural network for classification tasks from scratch.
To motivate the need for perceptron, let us consider the following problem. Suppose that we are given two sets of points in the X_{1}-X_{2} planes:
(1) 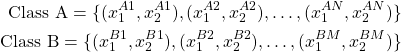
where
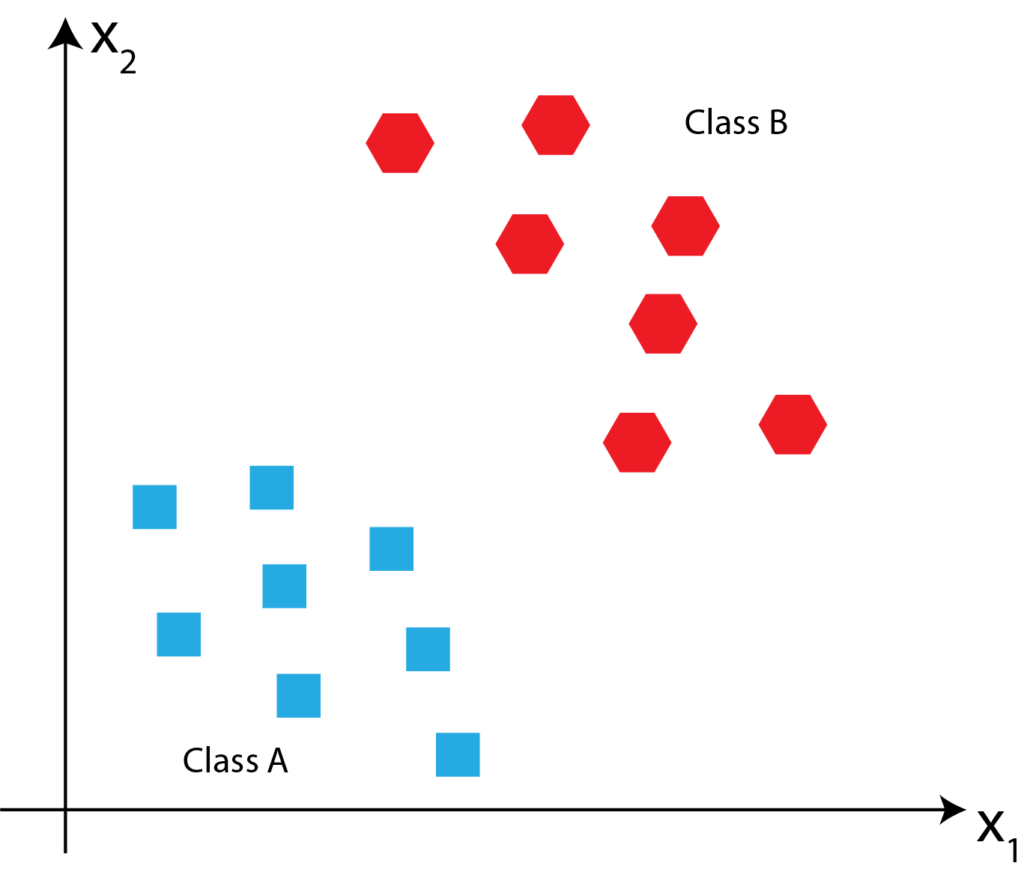
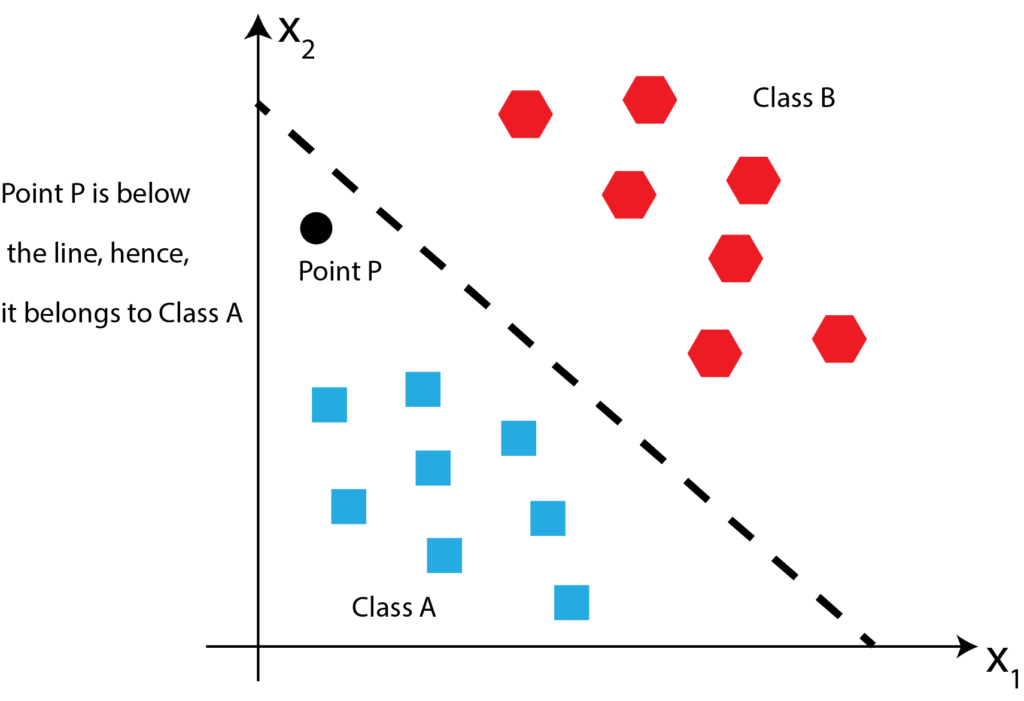
Now, suppose that we are given a new point P: ![]() . Our task is to determine if this point belongs to Class A or Class B? Point P is illustrated in the figure below.
. Our task is to determine if this point belongs to Class A or Class B? Point P is illustrated in the figure below.
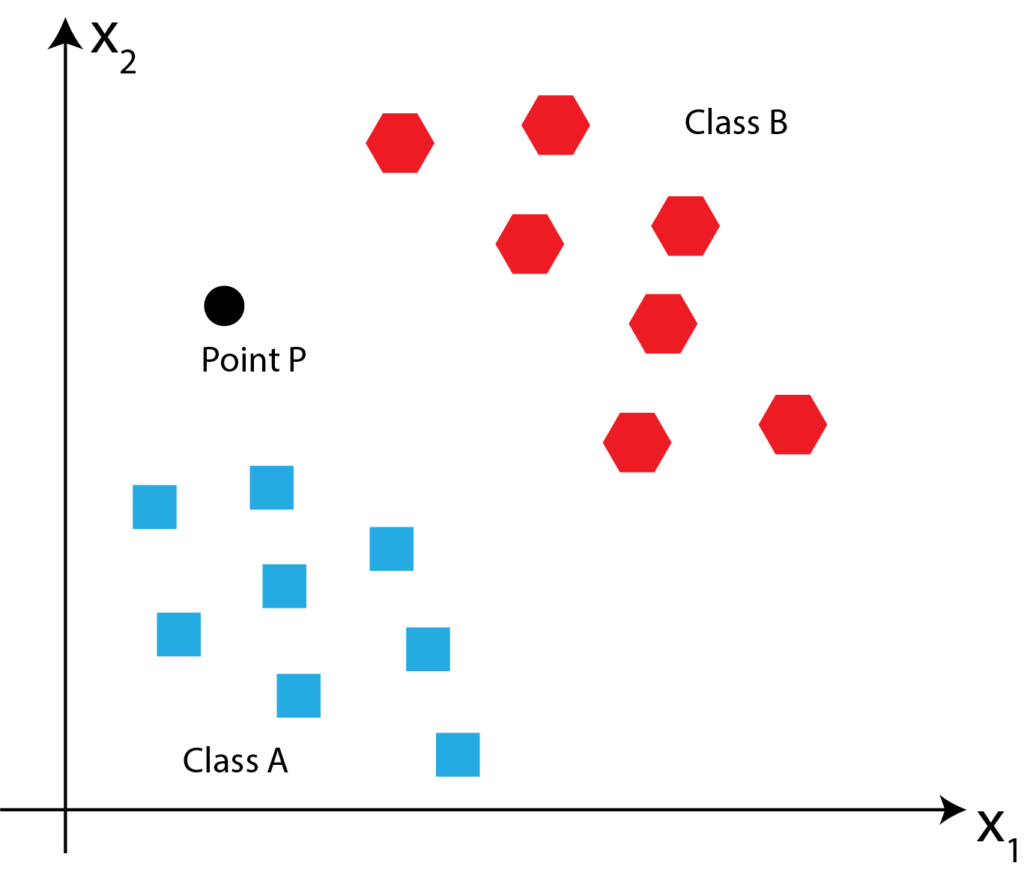
One way to solve this problem is to first fit the line that will separate these two classes, then once this line is fitted, we can easily determine where the point P belongs by investigating if the point P is above or below the fitted line. The fitted line is shown in the figure below.
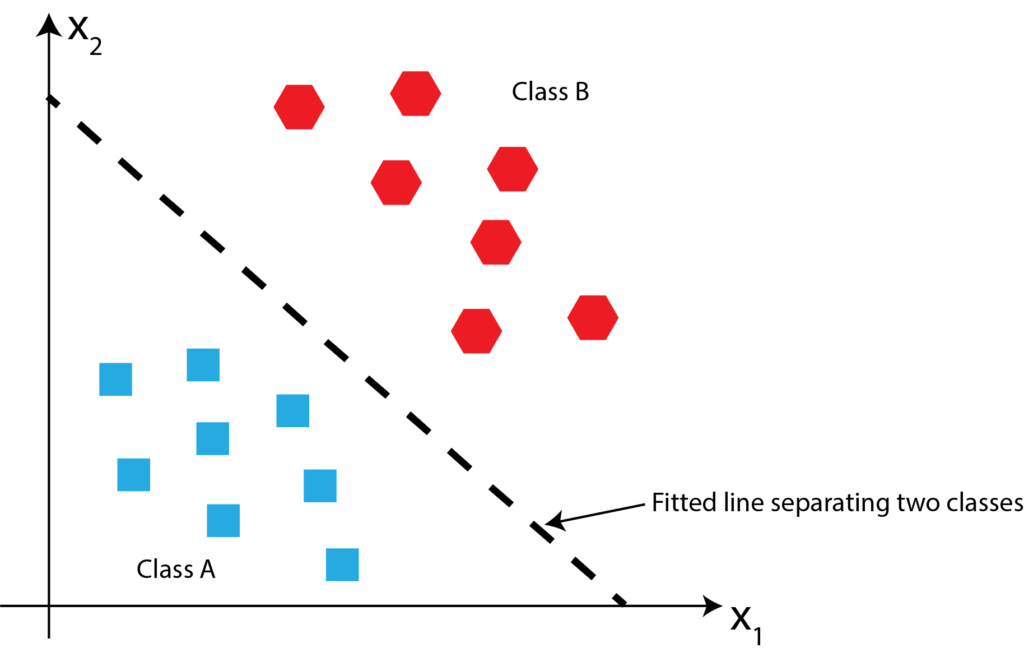
Since point P is below the fitted line, it belongs to class P. This is shown in the figure below.
Let us mathematically formulate this problem and explain how to solve it. First, let us define the line. In the general case, the line will have the following canonical form
(2) ![]()
where
With the line (2), we associate the net input function
(3) ![]()
This function can also be written in the vector form
(4) ![]()
where
(5) 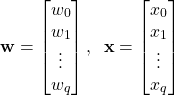
![]() is the vector of weights, and
is the vector of weights, and ![]() is the vector of features.
is the vector of features.
Now, for every point that is above the line, we have that ![]() . Similarly, for every point above the line, we have that
. Similarly, for every point above the line, we have that ![]() . To distinguish the two classes, we introduce the decision function
. To distinguish the two classes, we introduce the decision function ![]()
(6) 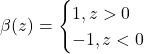
With every training sample ![]() , consisting of features
, consisting of features ![]() , we can associate the value
, we can associate the value ![]() that is equal to -1 if the point
that is equal to -1 if the point ![]() belongs to class A, or 1 if the point belongs to class B. Let us suppose that we have a total of
belongs to class A, or 1 if the point belongs to class B. Let us suppose that we have a total of ![]() samples of input features
samples of input features ![]() and output targets
and output targets ![]() ,
, ![]() .
.
Consequently, we can define the matrix of features and the vector of output targets as follows:
(7) 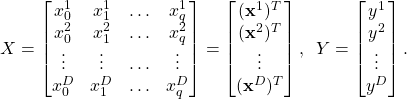
The algorithm for training the perceptron network, can be summarized as follows. First, we select the number of training epochs. Let this number be denoted by ![]() . Then, we select the inital values of the entries of the weight vector
. Then, we select the inital values of the entries of the weight vector ![]() . These values are either selected as zeros or as small random numbers. Also, we select the learning rate
. These values are either selected as zeros or as small random numbers. Also, we select the learning rate ![]() as a real number in the interval (0,1). Then, we repeat the following steps
as a real number in the interval (0,1). Then, we repeat the following steps ![]() times (that is we repeat them in every training epoch):
times (that is we repeat them in every training epoch):
For ![]() , (
, (![]() is the number of training samples), compute the following value
is the number of training samples), compute the following value
(8) ![]()
and update the weights
(9) ![]()
The value of ![]() represents the predicted class value computed on the basis on the current computed weights
represents the predicted class value computed on the basis on the current computed weights ![]() .
.
So the algorithm consists of two nested loops. The first outer loop is iterated over the training epoch ![]() , and the second inner loop is iterated over
, and the second inner loop is iterated over ![]() (training sample number), where in every inner loop we compute (8) and (9).
(training sample number), where in every inner loop we compute (8) and (9).