Forward Robot Kinematics Using Homogeneous Transform – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In our previous post, given here, we have explained how to define homogenous transforms to describe the rotation and translation of one coordinate system with respect to another. Homogeneous transform is actually a matrix that describes the translation and rotation of one coordinate system with respect to another one. In this post, we explain how to use homogeneous transform to solve a forward kinematics problem.

Consider a robotic manipulator with two degrees of freedom shown in the figure below

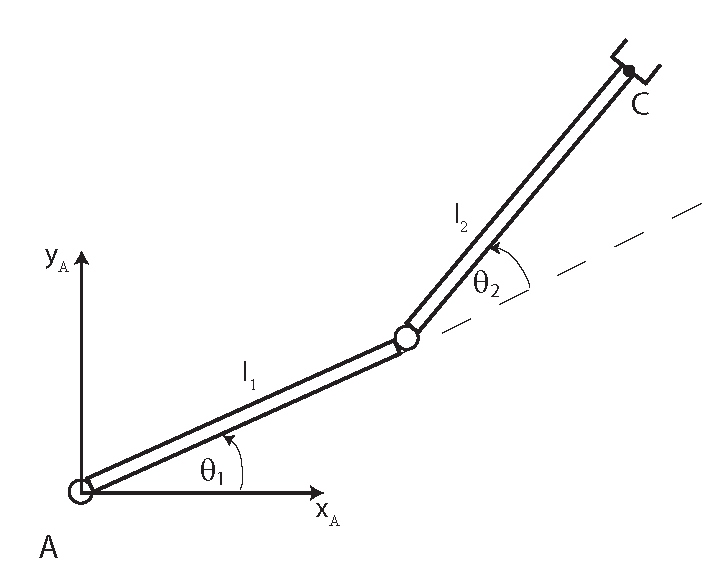
Figure 1: Two degrees of freedom robotic manipulator for illustrating the forward kinematics problem.

The forward kinematics problem can be postulated as follows:

Consider the robotic manipulator shown in Fig. 1. Given the joint coordinates $\theta_{1}$ and $\theta_{2}$ , and the link lengths $l_{1}$ and $l_{2}$ , compute the coordinates of the point $C$ (end-effector point) in the world coordinate system A.

Solution 1 (without using homogeneous transform):

We have:

(1) $\begin{align*}C_{x_{A}} =l_{1} cos(\theta_{1})+l_{2} cos(\theta_{1}+\theta_{2}) \\ C_{y_{A}} =l_{1} sin(\theta_{1})+l_{2} sin(\theta_{1}+\theta_{2}) \end{align*}$

where $C_{x_{A}}$ and $C_{y_{A}}$ are the x and y coordinates of the point $C$ in the world coordinate system $A$ . Now, let us recall basic trigonometric formulas:

(2) $\begin{align*} cos(\theta_{1}+\theta_{2}) =cos( \theta_{1} ) cos( \theta_{2} ) - sin( \theta_{1} ) sin( \theta_{2} ) \\ sin(\theta_{1}+\theta_{2}) =sin( \theta_{1} ) cos( \theta_{2} ) + cos( \theta_{1} ) sin( \theta_{2} ) \end{align*}$

By substituting these formulas in (3), we obtain

(3) $\begin{align*} C_{x_{A}} =l_{1} cos(\theta_{1})+l_{2} \Big( cos( \theta_{1} ) cos( \theta_{2} ) - sin( \theta_{1} ) sin( \theta_{2} ) \Big) \\ C_{y_{A}} =l_{1} sin(\theta_{1})+l_{2} \Big( sin( \theta_{1} ) cos( \theta_{2} ) + cos( \theta_{1} ) sin( \theta_{2} ) \Big) \end{align*}$

Solution 2 (by using homogeneous transform):

First, we assign coordinate systems. We assign a coordinate system to every axis (joint). The coordinate systems are shown in the figure below

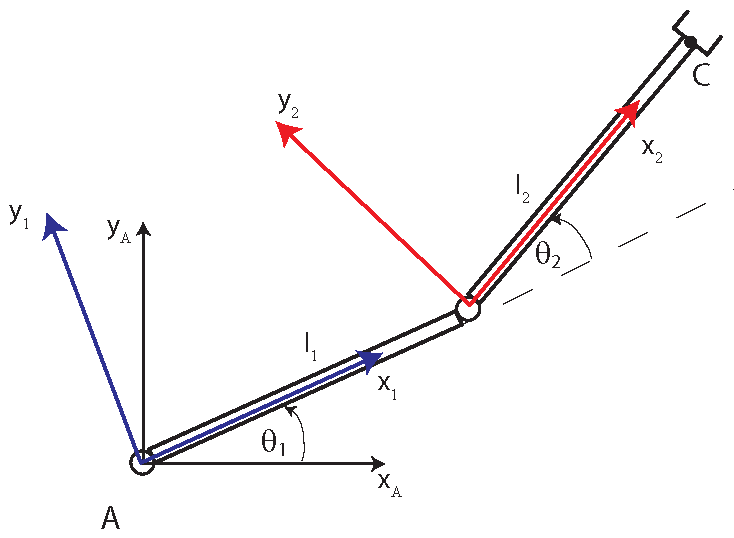
The point $C$ in the coordinate system $2$ has the following coordinates

(4) $\begin{align*} \leftindex^{2} \mathbf{C} =\begin{bmatrix} l_{2} \\ 0 \end{bmatrix}\end{align*}$

As we have explained in our previous post, the notation $\leftindex^{2} \mathbf{C}$ means that the coordinates of the vector $\mathbf{C}$ are represented in the coordinate system $2$ . On the other hand, we can assign homogeneous transformation, to represent the vector $\leftindex^{2}{C}$ in the coordinate system $1$ :

(5) $\begin{align*}\begin{bmatrix} \leftindex^{1}{\mathbf{C}} \\ 1\end{bmatrix} =\begin{bmatrix} \leftindex^{1}_{2}{R} & \leftindex^{1} {\mathbf{l}_{1}} \\ \mathbf{0}_{1\times 2} & 1 \end{bmatrix}\begin{bmatrix} \leftindex^{2}{\mathbf{C}} \\ 1 \end{bmatrix}\end{align*}$

where $\leftindex^{1} {\mathbf{l}_{1}}$ is the representation of the vector $\mathbf{l}_{1}$ in the coordinate system $1$

(6) $\begin{align*} \mathbf{l}_{1} =\begin{bmatrix} l_{1} \\ 0 \end{bmatrix}\end{align*}$

and the rotation matrix $\leftindex^{1}_{2}{R}$ is given by

(7) $\begin{align*} \leftindex^{1}_{2}{R} =\begin{bmatrix} cos(\theta_{2}) & -sin(\theta_{2}) \\ sin(\theta_{2}) & cos(\theta_{2}) \end{bmatrix}\end{align*}$

The notation $\leftindex^{1}_{2}{R}$ means that the rotation matrix represents transformation from the coordinate system $2$ to coordinate system $1$ (lower index means “from”, and the upper index means “to”). On the other hand, the representation of the vector $\leftindex^{1}{\mathbf{C}}$ in the coordinate system $A$ is given by another homogeneous transformation

(8) $\begin{align*} \begin{bmatrix} \leftindex^{A}{\mathbf{C}} \\ 1\end{bmatrix} =\begin{bmatrix} \leftindex^{A}_{1}{R} & \mathbf{0}_{2\times 1}\\ \mathbf{0}_{1\times 2} & 1 \end{bmatrix}\begin{bmatrix} \leftindex^{1}{\mathbf{C}} \\ 1 \end{bmatrix}\end{align*}$

where

(9) $\begin{align*} \leftindex^{A}_{1}{R} =\begin{bmatrix} cos(\theta_{1}) & -sin(\theta_{1}) \\ sin(\theta_{1}) & cos(\theta_{1}) \end{bmatrix}\end{align*}$

and the vector $\mathbf{0}_{2\times 1}$ is 2 times 1 vector of zeros, since the coordinate systems $A$ and $1$ are located at the same point, and consequently, there is no translation of coordinate systems. By combining (5) and (8), we obtain

(10) $\begin{align*}& \begin{bmatrix} \leftindex^{A}{\mathbf{C}} \\ 1 \end{bmatrix} = \begin{bmatrix} C_{x_{A}} \\ C_{y_{A}} \\ 1 \end{bmatrix} \\& =\begin{bmatrix} \leftindex^{A}_{1}{R} & \mathbf{0}_{2\times 1}\\ \mathbf{0}_{1\times 2} & 1 \end{bmatrix} \begin{bmatrix} \leftindex^{1}_{2}{R} & \leftindex^{1} {\mathbf{l}_{1}} \\ \mathbf{0}_{1\times 2} & 1 \end{bmatrix}\begin{bmatrix} \leftindex^{2}{\mathbf{C}} \\ 1 \end{bmatrix} = \begin{bmatrix} \leftindex^{A}_{1}{R} & \mathbf{0}_{2\times 1}\\ \mathbf{0}_{1\times 2} & 1 \end{bmatrix} \begin{bmatrix} \leftindex^{1}_{2}{R} & \leftindex^{1} {\mathbf{l}_{1}} \\ \mathbf{0}_{1\times 2} & 1 \end{bmatrix}\begin{bmatrix} l_{2} \\ 0 \\ 1 \end{bmatrix} \end{align*}$

That is

(11) $\begin{align*} & \begin{bmatrix} \leftindex^{A}{\mathbf{C}} \\ 1 \end{bmatrix} = \begin{bmatrix} C_{x_{A}} \\ C_{y_{A}} \\ 1 \end{bmatrix} \\ & = \begin{bmatrix} cos(\theta_{1}) & -sin(\theta_{1}) & 0 \\ sin(\theta_{1}) & cos(\theta_{1}) & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} cos(\theta_{2}) & -sin(\theta_{2}) & l_{1} \\ sin(\theta_{2}) & cos(\theta_{2}) & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} l_{2} \\ 0 \\ 1 \end{bmatrix} \\& = \begin{bmatrix} cos(\theta_{1}) & -sin(\theta_{1}) & 0 \\ sin(\theta_{1}) & cos(\theta_{1}) & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}l_{2}cos(\theta_{2}) +l_{1} \\ l_{2}sin(\theta_{2}) \\1 \end{bmatrix} \\ & = \begin{bmatrix} l_{2}cos(\theta_{1}) cos(\theta_{2}) +l_{1}cos(\theta_{1}) -l_{2}sin(\theta_{1}) sin(\theta_{2}) \\ l_{2}sin(\theta_{1}) cos(\theta_{2}) +l_{1}sin(\theta_{1}) +l_{2}cos(\theta_{1}) sin(\theta_{2}) \\ 1 \end{bmatrix}\end{align*}$

This result is identical to (3).

admin

You might also like

Backward Euler Discretization of State-Space Models in MATLAB

ENS459 Third Lab Assignment

Intuitive Understanding of Lyapunov’s Stability Analysis – 1D Example