In this control engineering and control theory tutorial, we explain how to easily solve the Lyapunov equation by using the Kronecker product. We provide a detailed explanation with Python codes.
The YouTube video tutorial accompanying this page is given here. All the codes are posted on our GitHub page given here.
Background on Lyapunov Equation and Kronecker Product
The Lyapunov equation for continuous-time systems has the following form:
(1) ![]()
where ![]() and
and ![]() are known matrices, and
are known matrices, and ![]() is the matrix that we want to determine. That is, we want to solve this system with respect to
is the matrix that we want to determine. That is, we want to solve this system with respect to ![]() . Often, it is assumed that the matrix
. Often, it is assumed that the matrix ![]() is positive definite, and often the matrix
is positive definite, and often the matrix ![]() is a system matrix of a linear dynamical system, such as the one described below
is a system matrix of a linear dynamical system, such as the one described below
(2) ![]()
where ![]() is the state vector. The Lyapunov equation and its solution
is the state vector. The Lyapunov equation and its solution ![]() are extensively used in control theory and control engineering practive. For example, the Lyapunov equation is important for stability analysis of dynamical systems, control system design, and for optimal control. It is important to emphasize that the solution of the Riccati matrix equation can be obtained by solving a series of Lyapunov equations. Consequently, the Lyapunov equation is very important for designing optimal controllers and for evaluating their stability. Here is the problem we want to solve:
are extensively used in control theory and control engineering practive. For example, the Lyapunov equation is important for stability analysis of dynamical systems, control system design, and for optimal control. It is important to emphasize that the solution of the Riccati matrix equation can be obtained by solving a series of Lyapunov equations. Consequently, the Lyapunov equation is very important for designing optimal controllers and for evaluating their stability. Here is the problem we want to solve:
Problem: Given the matrices ![]() and Q, determine the solution
and Q, determine the solution ![]() of the Lyapunov equation (1).
of the Lyapunov equation (1).
In a number of scenarios, we are not only seaching for any solution of the Lyapunov equation. Often, we are searching for a symmetric positive definite matrix ![]() . However, since this an introductory tutorial, we will not add this additional layer of complexity to the above problem. In fact, the solution found by the method presented in the sequel will actually be a symmetric and positive definite matrix. This is mainly because the particular Lyapunov equation that we will consider will have a unique solution and this unique solutin is a postive definite symmetric matrix.
. However, since this an introductory tutorial, we will not add this additional layer of complexity to the above problem. In fact, the solution found by the method presented in the sequel will actually be a symmetric and positive definite matrix. This is mainly because the particular Lyapunov equation that we will consider will have a unique solution and this unique solutin is a postive definite symmetric matrix.
Now, let us focus on the Kronecker product. Let ![]() and
and ![]() arbitrary matrices (
arbitrary matrices (![]() matrix in the following equation is not related to
matrix in the following equation is not related to ![]() matrix in the Lyapunov equation):
matrix in the Lyapunov equation):
(3) ![]()
Then, the Kronecker product is defined by following matrix
(4) 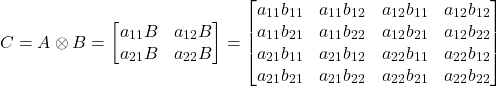
where ![]() is the symbol for the Kronecker product. The definition of the Kronecker product that is shown below is for 2 by 2 matrices. However, we can easily generalize the definition to matrices of arbitrary dimensions. Next, we need to introduce the vectorization operator. The vectorization operator creates a vector out of a matrix by stacking its column on top of each other. More precisely, let
is the symbol for the Kronecker product. The definition of the Kronecker product that is shown below is for 2 by 2 matrices. However, we can easily generalize the definition to matrices of arbitrary dimensions. Next, we need to introduce the vectorization operator. The vectorization operator creates a vector out of a matrix by stacking its column on top of each other. More precisely, let ![]() be the notation for the vectorization operator. Then, we have
be the notation for the vectorization operator. Then, we have
(5) 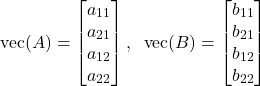
The vectorization operator and Kronecker product are related to each other. Namely, let us consider the following matrix equation
(6) ![]()
Let us apply the vectorization operator to both left-hand and right-hand sides of this equation:
(7) ![]()
Now, it can be shown that the following formula is valid
(8) ![]()
This formula is very important since if we want to solve the matrix equation (6) for the matrix ![]() , we can do that by solving the standard system of nonlinear equations given by the equation (8), where
, we can do that by solving the standard system of nonlinear equations given by the equation (8), where ![]() is now a vector.
is now a vector.
Solve the Lyapunov Equation by Using Kronecker Product
here, we will apply everything we learned in the previous section to the problem of solving the Lyapunog equation. Let us first apply the vectorization operator to our Lyapunov equation (1)
(9) ![]()
Since the vectorization operator is a linear operator, we have
(10) ![]()
Next, by using the formula (8), we have
(11) 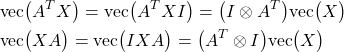
where ![]() is an identity matrix. By substituting these two formulas in (10), we obtain
is an identity matrix. By substituting these two formulas in (10), we obtain
(12) ![]()
Let us introduce the matrix ![]() as follows
as follows
(13) ![]()
Then, the last system can be writen as
(14) ![]()
Under the assumption that the matrix ![]() is invertible, the solution of this system is given by
is invertible, the solution of this system is given by
(15) ![]()
The solution (15) is the solution of our Lyapunov equation. Once we determine this solution we can de-vectorize ![]() and form the matrix
and form the matrix ![]() . Next, we explain the Python codes for solving the Lyapunov equation.
. Next, we explain the Python codes for solving the Lyapunov equation.
Python Codes for Solving the Lyapunov Equation
First, we explain how to compute the Kronecker product in Python, and how to perform the vectorization and de-vectorization. The following code lines are self-explanatory and they explain how to compute the Kronecker product, as well as how to vectorize and de-vecotorize matrices and vectors.
import numpy as np
import control as ct
# test of the Kronecker product in Python
Atest=np.array([[1,2],[3,4]])
Btest=np.array([[2,1],[3,4]])
Cmatrix=np.kron(Atest,Btest)
# test of vectorization
AtestVectorized=Atest.flatten('F').reshape(4,1)
np.matmul(Cmatrix,AtestVectorized)
# test of de-vectorization
Atest1=AtestVectorized.reshape(2,2,order='F')
Here, we need to mention that we are using the NumPy library for matrix computations, and we are using the Python control systems library in order to construct the matrix ![]() of a stable system. We import the control systems library as ct. You can install the control system library from a terminal or from an Anaconda terminal by typing “pip install control“.
of a stable system. We import the control systems library as ct. You can install the control system library from a terminal or from an Anaconda terminal by typing “pip install control“.
The following Python code lines are used to construct a stable transfer function, and then to transform this transfer function into a state-space model, and then to extract the matrix ![]() from this state-space model. This matrix
from this state-space model. This matrix ![]() is used in the Lyapunov equation as the coefficient matrix. To construct the stable transfer funtion, we using the function “ct.zpk()”. This function will construct a transfer function with specified zeros, poles, and gain (“zpk”- zero, pole, and gain).
is used in the Lyapunov equation as the coefficient matrix. To construct the stable transfer funtion, we using the function “ct.zpk()”. This function will construct a transfer function with specified zeros, poles, and gain (“zpk”- zero, pole, and gain).
# now test the Lyapunov Equation solution
# define a stable transfer function
tfTest = ct.zpk([1], [-1,-2,-3], gain=1)
print(tfTest)
# create a state-space model
ssTest=ct.tf2ss(tfTest)
print(ssTest)
# extract the A matrix
A=ssTest.A
The following piece of code will first verify that the matrix ![]() is stable by computing its eigenvalues. Them, the code will construct a positive definite matrix
is stable by computing its eigenvalues. Them, the code will construct a positive definite matrix ![]() that is the right-hand side of the Lyapunov equation. Then, the code will vectorize the Lyapunov equation and compute its vectorized solution (15). Then, this solution will be de-vectorized to obtain the final matrix
that is the right-hand side of the Lyapunov equation. Then, the code will vectorize the Lyapunov equation and compute its vectorized solution (15). Then, this solution will be de-vectorized to obtain the final matrix ![]() . Then, the code will verify the accuracy of the solution by computing
. Then, the code will verify the accuracy of the solution by computing
(16) ![]()
This complete expression should be equal to zero or very close to zero if the solution ![]() is accurately computed. In that way, we can quantify how accurate is the solution
is accurately computed. In that way, we can quantify how accurate is the solution ![]() .
.
# check the eigenvalues of A
np.linalg.eig(A)
# create the matrix Q that is positive definite
Q=np.array([[10, -0.2, -0.1],[-0.2, 20, -0.2],[-0.1, -0.2, 3]])
# Lyapunov equation A'*X+X*A=-Q
Qvectorized=Q.flatten('F').reshape(9,1)
S=np.kron(np.eye(3,3),A.T)+np.kron(A.T,np.eye(3,3))
Xvectorized=-np.matmul(np.linalg.inv(S),Qvectorized)
X=Xvectorized.reshape(3,3,order='F')
# check the eigenvalues
np.linalg.eig(X)
# confirm that the solution actually satisfies
# Lyapunov equation A'*X+X*A=-Q
# LHS=A'*X+X*A
# LHS+Q=0 -> equivalent form
# the Lyapunov equation
LHS=np.matmul(A.T,X)+np.matmul(X,A)
# this should be zero or close to zero if X is the
# correct solution
LHS+Q