This is the second part of the tutorial series on particle filters. In this tutorial part, we derive the particle filter algorithm from scratch. Here are all the tutorials in this series (click on the link to access the tutorial webpage):
PART 2: You are currently reading Part 2. In Part 2 we derive the particle filter algorithm from scratch.
PART 3: In part 3, we explain how to implement the particle filter algorithm in Python from scratch.
In this tutorial part, first, we briefly revise the big picture of particle filters. Then, we briefly revise the main results from probability and statistics that a student needs to know in order to understand the derivation of particle filters. Then, we derive the particle filter algorithm. Finally, we concisely summarize the particle filter algorithm. Before reading this tutorial part, it is suggested to go over the first tutorial part.
The YouTube tutorial accompanying this webpage is given below.
Big Picture of Particle Filters – Approximation of Posterior Probability Density Function of State Estimate
As explained in the first tutorial part, for presentation clarity and not to blur the main ideas of particle filters with too many control theory details, we develop a particle filter for the linear state-space model given by the following two equations:
(1) ![]()
where ![]() is the state vector at the discrete time step
is the state vector at the discrete time step ![]() ,
, ![]() is the control input vector at the time step
is the control input vector at the time step ![]() ,
, ![]() is the process disturbance vector (process noise vector) at the time step
is the process disturbance vector (process noise vector) at the time step ![]() ,
, ![]() is the observed output vector at the time step
is the observed output vector at the time step ![]() ,
, ![]() is the measurement noise vector at the discrete time step
is the measurement noise vector at the discrete time step ![]() , and
, and ![]() ,
, ![]() , and
, and ![]() are system matrices.
are system matrices.
In the first tutorial part, we explained that the main goal of particle filters is to recursively approximate the state posterior probability density function, denoted by
(2) ![]()
where ![]() and
and ![]() denote the sets of inputs and outputs
denote the sets of inputs and outputs
(3) ![]()
In the particle filter and robotics literature, the posterior density is also called the filtering density (filtering distribution) or the marginal density (marginal distribution). Some researchers call the density ![]() as the posterior density (this density will be formally introduced later on in this tutorial), and they refer to the density
as the posterior density (this density will be formally introduced later on in this tutorial), and they refer to the density ![]() as the filtering density or as the marginal density. However, we will not follow this naming convention. We refer to
as the filtering density or as the marginal density. However, we will not follow this naming convention. We refer to ![]() as the posterior density, and we refer to the density
as the posterior density, and we refer to the density ![]() as the smoothing density. This is mainly because the density
as the smoothing density. This is mainly because the density ![]() takes the complete state sequence into account, and this fact means that estimates are smoothed.
takes the complete state sequence into account, and this fact means that estimates are smoothed.
At the time instant ![]() , the particle filter computes the set of particles
, the particle filter computes the set of particles
(4) ![]()
A particle with the index of ![]() consists of the tuple
consists of the tuple ![]() , where
, where ![]() is the state sample, and
is the state sample, and ![]() is the importance weight. The set of particles approximates the posterior distribution as follows
is the importance weight. The set of particles approximates the posterior distribution as follows
(5) 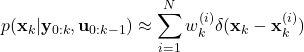
where ![]() is the Dirac delta function that is shifted and centered at
is the Dirac delta function that is shifted and centered at ![]() .
.
The particle filter design problem is to design an update rule (update functions) for particles that will update the particles from the time step ![]() to the time step
to the time step ![]() :
:
(6) 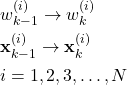
where the update rule should incorporate the observed output ![]() , control input
, control input ![]() , state-space model (1), state transition probability, and measurement probability (see the first tutorial part for the precise definitions of these probabilities).
, state-space model (1), state transition probability, and measurement probability (see the first tutorial part for the precise definitions of these probabilities).
Once we have the approximation of the posterior distribution (5), we can approximate the mean and variance of the estimate, as well as any statistics, such as higher-order moments or confidence intervals.
Basic Results from Statistics and Probability Necessary to Know For Deriving the Particle Filter
To develop the particle filter algorithm, it is important to know the basic rules of probability and the Bayes’ theorem. Here, we briefly revise the main results from the probability theory you need to know in order to understand the derivation of the particle filter algorithm. Let ![]() be an arbitrary conditional probability density function, and let
be an arbitrary conditional probability density function, and let ![]() , and
, and ![]() be two vectors. Then, we have
be two vectors. Then, we have
(7) ![]()
or
(8) ![]()
On the other hand, we also have
(9) ![]()
By combining (8) and (9), we have
(10) ![]()
From the last equation, we obtain
(11) ![]()
The equation represents the mathematical formulation of Bayes’ theorem or Bayes’ rule. Although it looks simple, this is one of the most important and fundamental results in statistics and probability.
In the context of the Bayesian estimation, we want to infer statistics or an estimate of ![]() from the observation
from the observation ![]() . The density
. The density ![]() is called the posterior and we want to compute this density. The density
is called the posterior and we want to compute this density. The density ![]() is called the likelihood. The density
is called the likelihood. The density ![]() is called the prior density, and the density
is called the prior density, and the density ![]() is called the marginal density. Usually, the marginal density is not important and it serves as a normalizing factor. Consequently, the Bayes’ rule can be written as
is called the marginal density. Usually, the marginal density is not important and it serves as a normalizing factor. Consequently, the Bayes’ rule can be written as
(12) ![]()
where ![]() is the normalizing constant. The Bayes rule can be also expanded to the cases of three or more vectors. For example, if we would have three vectors
is the normalizing constant. The Bayes rule can be also expanded to the cases of three or more vectors. For example, if we would have three vectors ![]() ,
, ![]() , and
, and ![]() , the Bayes’ rule takes this form
, the Bayes’ rule takes this form
(13) ![]()
or in the normalized form
(14) ![]()
Derivation of Particle Filter Algorithm
After revising the basics of the Bayes’ rule, let us now go back to the derivation of the particle filter. We start from the probability density function that takes into account all the states starting from ![]() and ending at
and ending at ![]() :
:
(15) ![]()
where ![]() ,
, ![]() , and
, and ![]() are sets defined as follows
are sets defined as follows
(16) 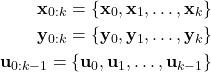
This density takes into account the complete state-sequence ![]() . That is, the complete state sequence is
. That is, the complete state sequence is ![]() is seen as a random “variable” or “augmented random vector” that we want to estimate. By knowing the mathematical form of this density, we can easily derive the posterior distribution (5). The density (15) is often called the smoothing posterior density. The particle filter is derived by first considering the expectation involving the smoothing density
is seen as a random “variable” or “augmented random vector” that we want to estimate. By knowing the mathematical form of this density, we can easily derive the posterior distribution (5). The density (15) is often called the smoothing posterior density. The particle filter is derived by first considering the expectation involving the smoothing density
(17) ![]()
where ![]() is a nonlinear function of the state sequence,
is a nonlinear function of the state sequence, ![]() is the expectation operator, and
is the expectation operator, and ![]() is the state support (domain) of the smoothed posterior density.
is the state support (domain) of the smoothed posterior density.
This equation is the expectation of the (vector) function of the state sequence ![]() computed under the assumption that the state sequence is distributed according to the posterior smoothed density
computed under the assumption that the state sequence is distributed according to the posterior smoothed density ![]() . Note here that
. Note here that ![]() is defined as a set in (16). However, we are also using
is defined as a set in (16). However, we are also using ![]() as a variable. This is a slight abuse of notation that is necessary in order to ease the notation complexity in this tutorial and to make the tutorial as clear as possible. You can think of
as a variable. This is a slight abuse of notation that is necessary in order to ease the notation complexity in this tutorial and to make the tutorial as clear as possible. You can think of ![]() as a vector that is formed by stacking (augmenting) the states
as a vector that is formed by stacking (augmenting) the states ![]() on top of each other.
on top of each other.
The equation (17) is the most important equation for us. The main purpose of the estimation process is to compute an approximation of the smoothed posterior density that will enable us to compute this integral. Namely, if we would know the smoothed posterior density, then we would be able at least in theory (keep in mind that solving an expectation integral can sometimes be a very difficult task) to approximate any statistics of the smoothed posterior state estimate. For example, if we want to compute the mean of the estimated state sequence ![]() , then
, then ![]() .
.
However, we do not know the smoothed posterior density ![]() , and we cannot compute or approximate this expectation integral.
, and we cannot compute or approximate this expectation integral.
Here comes the first remedy for this problem (we will need several remedies). The remedy is to use the importance sampling method. In our previous tutorial, given here, we explained the basics of the importance sampling method. The main idea of the importance sampling is to select a new density or a function denoted by ![]() (called as the proposal density), and to approximate the integral (17) as follows
(called as the proposal density), and to approximate the integral (17) as follows
(18) ![Rendered by QuickLaTeX.com \begin{align*}E[\boldsymbol{\beta}(\mathbf{x}_{0:k})|\mathbf{y}_{0:k},\mathbf{u}_{0:k-1}] \approx \sum_{i=1}^{N}\tilde{w}_{k}^{(i)} \boldsymbol{\beta}(\mathbf{x}_{0:k}^{(i)}) \end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-c613a5eb6f8d8772f8ccbe0561a50c5c_l3.png)
where ![]() is a sample of the state sequence
is a sample of the state sequence ![]() sampled from the smoothed proposal (importance) density
sampled from the smoothed proposal (importance) density ![]() , and the weight is defined by
, and the weight is defined by
(19) 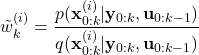
the general form of the weight is
(20) ![]()
What did we achieve with this strategy? First of all, notice that we did not use the unknown smoothed posterior distribution to generate the state sequence samples ![]() . We generated the state sequence samples
. We generated the state sequence samples ![]() from the smoothed proposal distribution with the density of
from the smoothed proposal distribution with the density of ![]() . We can generate these samples since we have complete freedom to select the proposal density. So one part of the issue is resolved.
. We can generate these samples since we have complete freedom to select the proposal density. So one part of the issue is resolved.
However, the unknown smoothed posterior is used to compute the weights ![]() . If we can somehow compute the weights without explicitly using the smoothed posterior distribution
. If we can somehow compute the weights without explicitly using the smoothed posterior distribution ![]() , then, we can approximate the original expectation without using the smoothed posterior distribution. From this fact, we conclude that the key to the computation of the expectation is to compute the weight
, then, we can approximate the original expectation without using the smoothed posterior distribution. From this fact, we conclude that the key to the computation of the expectation is to compute the weight ![]() without explicit knowledge of the smoothed posterior density. In the sequel, we show that this is indeed possible.
without explicit knowledge of the smoothed posterior density. In the sequel, we show that this is indeed possible.
To summarize: the main idea of the particle filter derivation is to derive the recursive equation for the weight ![]() . From the recursive equation for the weight
. From the recursive equation for the weight ![]() of the smoothed posterior density, we will be able to derive the recursive equation for the importance weight
of the smoothed posterior density, we will be able to derive the recursive equation for the importance weight ![]() of the original posterior density
of the original posterior density ![]() .
.
Let us now start with the derivation of the recursive relation for ![]() . We can formally write the smoothing density as follows
. We can formally write the smoothing density as follows
(21) ![]()
Then, by using Bayes’ rule, we have
(22) ![]()
where ![]() is the normalization factor explained previously. Next, since the state-space model is a Markov state-space model, we have
is the normalization factor explained previously. Next, since the state-space model is a Markov state-space model, we have
(23) ![]()
This is the direct consequence of the form of the output equation of the state-space model (1). The distribution of the output only depends on the state and measurement noise at the time step ![]() . The density
. The density ![]() is the measurement probability density function explained in the first tutorial part.
is the measurement probability density function explained in the first tutorial part.
By substituting (23) in (22), we obtain
(24) ![]()
Next, we can write
(25) ![]()
Next, we can use (8) to write the density ![]() as follows
as follows
(26) ![]()
Next, since the state-space model is Markov, the probability density ![]() is
is
(27) ![]()
This is because of the structure of the state equation of (1). The probability density function of the state at the time instant ![]() depends only on the state and input at the time step
depends only on the state and input at the time step ![]() . The density
. The density ![]() in (27) is the state transition density of the state-space model introduced in the first tutorial part.
in (27) is the state transition density of the state-space model introduced in the first tutorial part.
On the other hand, the density ![]() should not depend on the input
should not depend on the input ![]() . This is because from the state equation of (1) it follows that the state at the time instant
. This is because from the state equation of (1) it follows that the state at the time instant ![]() depends on
depends on ![]() and not on
and not on ![]() . That is, we have
. That is, we have
(28) ![]()
By substituting (27) and (28) in (26), we obtain
(29) ![]()
By substituting (29) in (25), we obtain
(30) ![]()
The expression (30) is important since it establishes a recursive relation for the probability density ![]() . Namely, we can observe that the density
. Namely, we can observe that the density ![]() , depends on its previous value at the time step
, depends on its previous value at the time step ![]() , measurement density, and the state transition density. This recursive relation is very important for deriving the recursive expression for the importance weight
, measurement density, and the state transition density. This recursive relation is very important for deriving the recursive expression for the importance weight ![]() .
.
Next, we need to derive a recursive equation for the smoothed proposal density (also known as smoothed importance density). Again, we start from the general form of the proposal density that takes into account the complete state sequence ![]() :
:
(31) ![]()
This density can be written as
(32) ![]()
Next, by using (8), we have
(33) ![]()
Since the proposal density is not strictly related to our dynamical system, the Markov property does not hold by default. However, we can always make an assumption that similar to the Markov property. Consequently, we assume
(34) ![]()
Also, the conditional density ![]() does not depend on the future output
does not depend on the future output ![]() . Also, this density does not depend on the input
. Also, this density does not depend on the input ![]() . This is because from the state equation of the model (1) it follows that the last state in the sequence
. This is because from the state equation of the model (1) it follows that the last state in the sequence ![]() , that is the state
, that is the state ![]() , does not depend on
, does not depend on ![]() . Instead, the state
. Instead, the state ![]() depends on
depends on ![]() . Consequently, we have that the conditional density has the following form
. Consequently, we have that the conditional density has the following form
(35) ![]()
By substituting (34) and (35) in (33), we obtain the final equation for the batch importance density:
(36) ![]()
We see that the smoothed proposal density ![]() depends on its value at the time step
depends on its value at the time step ![]() and
and ![]() . This important conclusion and derivation enables us to develop a recursive relation for the weight
. This important conclusion and derivation enables us to develop a recursive relation for the weight ![]() , and consequently, for the weight
, and consequently, for the weight ![]() .
.
Now, we can substitute the recursive relations given by (30) and (36) into the equation for the importance weight (20) of the smoothed posterior density
(37) 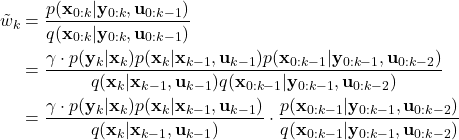
The last term in the last equation is actually the value of the weight of the smoothed posterior density at the time step ![]() :
:
(38) ![]()
Consequently, we can write (37) as follows
(39) ![]()
Here, it is important to observe the following:
We can compute the weight ![]() without knowing the full state trajectory
without knowing the full state trajectory ![]() or the previous input trajectory
or the previous input trajectory ![]() . The information that is necessary to compute the weight is stored in
. The information that is necessary to compute the weight is stored in ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Due to this, from (39), it follows that the importance weight
. Due to this, from (39), it follows that the importance weight ![]() of the posterior density
of the posterior density ![]() satisfies the following equation
satisfies the following equation
(40) ![]()
where ![]() is the proportionality symbol that is often used in probability and statistics to denote that one distribution or a quantity is proportional to another one. Here, we used the proportionality symbol instead of equality. This is done since we need to introduce a normalization factor that will ensure that all the weights
is the proportionality symbol that is often used in probability and statistics to denote that one distribution or a quantity is proportional to another one. Here, we used the proportionality symbol instead of equality. This is done since we need to introduce a normalization factor that will ensure that all the weights ![]() ,
, ![]() sum up to
sum up to ![]() . In practice, we first compute the right-hand side (40)
. In practice, we first compute the right-hand side (40)
(41) 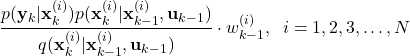
and we normalize these computed quantities to obtain ![]() . This will be explained in more detail in the sequel.
. This will be explained in more detail in the sequel.
Now that we know how the weights should be computed in the recursive manner, we need to address the following problem.
We can observe that in order to compute the weight (40), we need to know the density (function) ![]() . How to select this function?
. How to select this function?
The idea is to select this function such that
- We can easily draw samples from the distribution corresponding to this density.
- The expression for the weights (40) simplifies.
One of the simplest possible particle filters, called the bootstrap particle filter or the Sequential Importance Resampling (SIR) filter selects this function as the state transition density
(42) ![]()
By substituting (42) in (40), we obtain
(43) ![]()
This implies that for the sample ![]() , the weight
, the weight ![]() is computed as follows
is computed as follows
(44) ![]()
That is, the weight is computed by using the previous value of the weight and the value of the measurement density at the sample ![]() (also, the weight should be normalized). Here, it should be kept in mind that samples
(also, the weight should be normalized). Here, it should be kept in mind that samples ![]() should be sampled from the distribution with the density
should be sampled from the distribution with the density ![]() . That is, the samples are selected from the state transition probability (state transition distribution). The computed weights are used to approximate the posterior distribution given by the equation (5).
. That is, the samples are selected from the state transition probability (state transition distribution). The computed weights are used to approximate the posterior distribution given by the equation (5).
Now, we are ready to formulate the particle filter algorithm.
Particle Filter Algorithm
First, we state the algorithm, and then, we provide detailed comments about every step of the algorithm.
STATMENT OF THE SIR (BOOTSTRAP) PARTICLE FILTER ALGORITHM: For the initial set of particles
(45) ![]()
Perform the following steps for ![]()
- STEP 1: Using the state samples
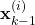 ,
, 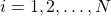 , computed at the previous step
, computed at the previous step 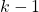 , at the time step
, at the time step  generate
generate 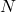 state samples
state samples 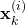 ,
, 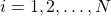 , from the state transition probability with the density of
, from the state transition probability with the density of 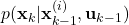 . That is,
. That is, (46)
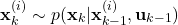
- STEP 2: By using the observed output
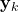 , and the weight
, and the weight 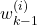 computed at the previous time step
computed at the previous time step 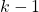 , calculate the intermediate weight update, denoted by
, calculate the intermediate weight update, denoted by 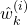 , by using the density function of the measurement probability
, by using the density function of the measurement probability(47)
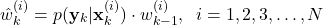
After all the intermediate weights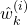 ,
, 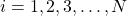 are computed, compute the normalized weights
are computed, compute the normalized weights 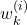 as follows
as follows(48)
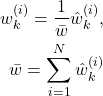
After STEP 1 and STEP 2, we computed the set of particles for the time step
(49)
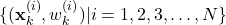
- STEP 3 (RESAMPLING): This is a resampling step that is performed only if the condition given below is satisfied. Calculate the constant
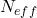
(50)
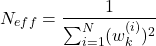
If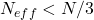 , then generate a new set of
, then generate a new set of 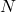 particles from the computed set of particles
particles from the computed set of particles(51)
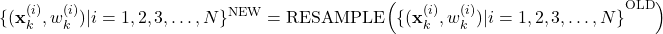
by using a resampling method (see the comments below). In (51), the “OLD” set of particles is the set of particles computed after STEP 1 and STEP 2, that is, the set given in (49).
Algorithm Explanation: We initialize the algorithm with an initial set of particles. This set of particles can be obtained by generating initial state samples from some distribution that covers the expected range of initial states and computing the weights. For example, we can assume a uniform distribution and we can assign equal weights to all the points generated from a uniform distribution.
In step 1 of the algorithm, for the given value of the state sample ![]() that is computed at the previous time
that is computed at the previous time ![]() step of the algorithm, and for the given input value
step of the algorithm, and for the given input value ![]() , we generate a state sample
, we generate a state sample ![]() from the state transition distribution. As explained in our previous tutorial, this step consists of generating a sample of a process noise vector in (1), and by computing
from the state transition distribution. As explained in our previous tutorial, this step consists of generating a sample of a process noise vector in (1), and by computing ![]() by using the state equation of the model (1).
by using the state equation of the model (1).
In step 2 of the algorithm, we first compute intermediate (not-normalized) weights ![]() . To do that, we use the weights
. To do that, we use the weights ![]() from the previous time step
from the previous time step ![]() of the algorithm, and the value of the measurement density that is computed for the current output measurement
of the algorithm, and the value of the measurement density that is computed for the current output measurement ![]() and the state sample
and the state sample ![]() computed at step 1 of the algorithm. After we compute all the intermediate weights, we simply normalize them to compute the weights
computed at step 1 of the algorithm. After we compute all the intermediate weights, we simply normalize them to compute the weights ![]() .
.
Step 3 of the algorithm is performed only if the condition stated above is satisfied. If the condition is satisfied, we need to resample our particles. Here is the reason for resampling. It often happens that after several iterations of the particle filter algorithm, we will have one or only a few particles with non-negligible weights. This means that most of the weights of particles will have a very small value. Effectively, this means that the weights of these particles are equal to zero. This is the so-called degeneracy problem in particle filtering. Since the time propagation of every particle consumes computational resources, we waste computational resources by propagating particles with very small weights. One of the most effective approaches to deal with the degeneracy problem is to resample particles. This means that we generate a new set of ![]() particles from the original set of particles. We will thoroughly explain two resampling approaches in the third part of this tutorial. One of the approaches for selecting particles from the original particle set (called “OLD” in the algorithm) is based on selecting
particles from the original set of particles. We will thoroughly explain two resampling approaches in the third part of this tutorial. One of the approaches for selecting particles from the original particle set (called “OLD” in the algorithm) is based on selecting ![]() state samples with replacements from the original set. The probability of selecting the sample
state samples with replacements from the original set. The probability of selecting the sample ![]() is proportional to its weight
is proportional to its weight ![]() in the “OLD” particle set. That is, we draw samples from the probability whose density is actually an approximation of the posterior density (5) at the time step
in the “OLD” particle set. That is, we draw samples from the probability whose density is actually an approximation of the posterior density (5) at the time step ![]() . After, we draw samples, we set their weights to
. After, we draw samples, we set their weights to ![]() . That is, we reset the weights. Since this type of resampling can have multiple instances of the same state sample in the new set, when we add their weights, we can actually obtain the final weight of the given state sample for the approximation of the posterior distribution. However, this is only done after all the time steps (time iterations) of the particle filter are completed, and when we finally want to extract an approximation of the posterior distribution. More about this in the third tutorial part.
. That is, we reset the weights. Since this type of resampling can have multiple instances of the same state sample in the new set, when we add their weights, we can actually obtain the final weight of the given state sample for the approximation of the posterior distribution. However, this is only done after all the time steps (time iterations) of the particle filter are completed, and when we finally want to extract an approximation of the posterior distribution. More about this in the third tutorial part.