In this optimization, scientific computing, and Python programming tutorial you will learn
- How to automatically compute gradients of multivariable functions in Python by using Python’s symbolic computation library called SymPy.
- How to automatically generate Python functions and how to automatically generate Python scripts that will return the gradients for given input vectors.
The programming techniques that you will learn in this tutorial are very important for the development of optimization, control, and signal processing algorithms. For example, you can use the techniques presented in this video tutorial to implement advanced optimization methods and to automatically define and implement the cost functions and gradients. The YouTube video accompanying this tutorial is given below.
Brief Summary of Gradients of Functions
Before we explain how to compute the gradients in Python, it is first important to briefly summarize and revise the concept of gradients of multivariable functions.
First, let us consider the following function
(1) ![]()
where ![]() and
and ![]() are independent variables, and
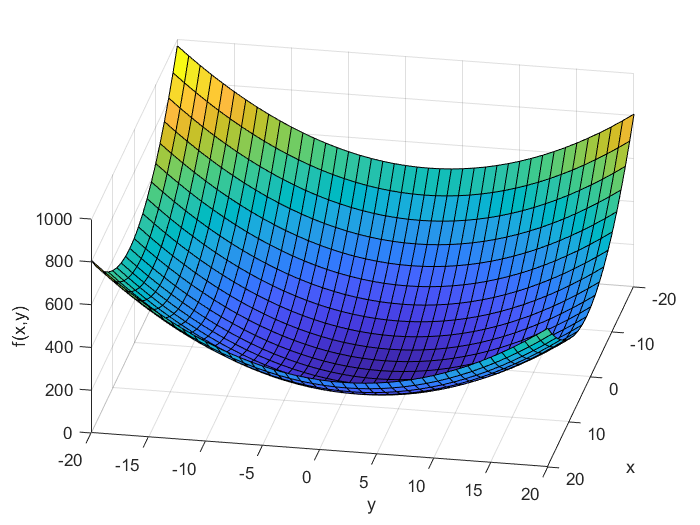
are independent variables, and ![]() is the function value. This function is shown in the figure below.
is the function value. This function is shown in the figure below.
In the general case, the gradient of a function of two variables is a vector defined by
(2) 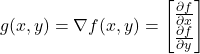
where
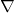 (nabla) is a mathematical symbol for the gradient.
(nabla) is a mathematical symbol for the gradient.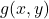 is the notation for the gradient vector.
is the notation for the gradient vector.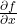 and
and 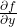 are the partial derivatives of
are the partial derivatives of 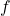 with respect to
with respect to 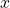 and
and 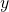 .
.
Next, let us compute the gradient of (1). The gradient is given by
(3) 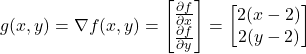
Next, let us compute the gradient at the point ![]() . The gradient at this point is equal to
. The gradient at this point is equal to
(4) ![]()
This gradient vector is shown in the figure below (red arrow).
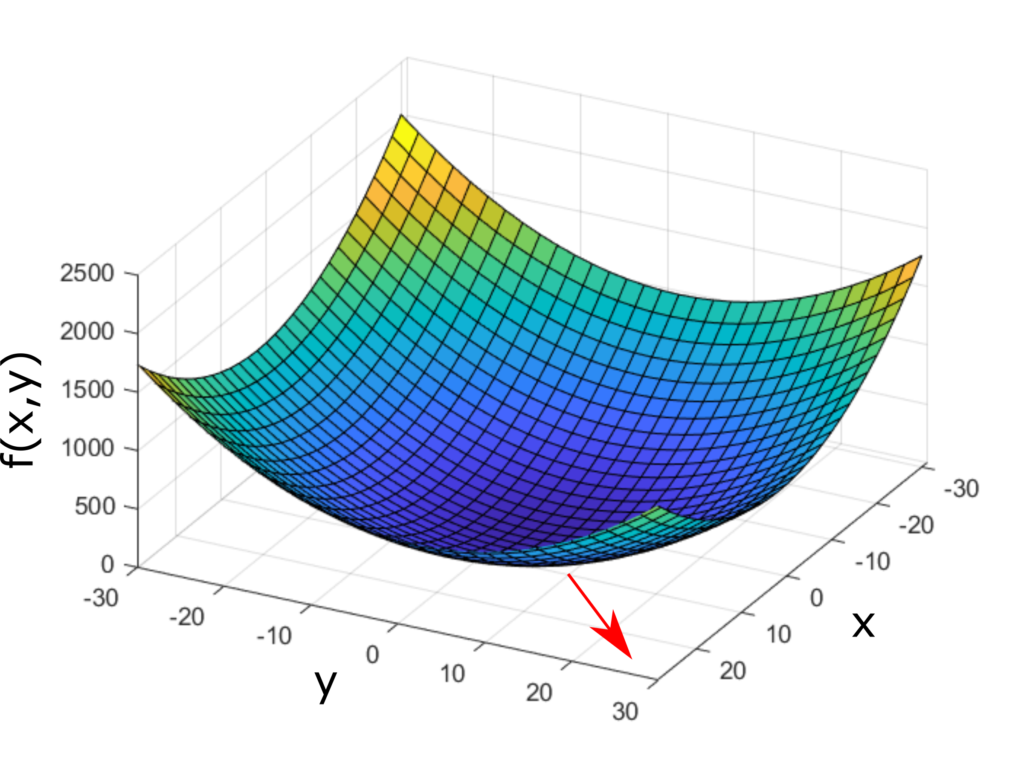
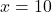 and
and 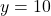 . The gradient is illustrated by the red arrow.
. The gradient is illustrated by the red arrow.Next, let us generalize the gradient definition. In the general case, the function ![]() depends on the
depends on the ![]() variables:
variables: ![]() ,
, ![]() , …,
, …, ![]() :
:
(5) ![]()
The gradient of the function ![]() is the
is the ![]() -dimensional vector
-dimensional vector
(6) 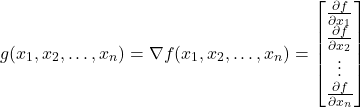
Automatic Computation of Gradients in Python
To compute the gradients, we use Python’s symbolic computation library called SymPy. First, let us explain how to compute the gradients of the function
(7) ![]()
The gradients are given by
(8) ![]()
The gradients in Python are computed as follows
# -*- coding: utf-8 -*-
"""
Computation of Symbolic Gradients in Python and
Automatic Generation of Python Functions for Gradients
"""
import numpy as np
from sympy import *
init_printing()
# symbolic state vector
x = MatrixSymbol('x',2,1)
# nonlinear function
f=Matrix([(x[0]-2)**2+(x[1]-2)**2])
# compute the gradient
g=f.jacobian(x)
# compute the transpose
g=g.transpose()First, we import the necessary functions and libraries. Then, we define the symbolic vector “x”. The entries of this vector are symbolic versions of ![]() and
and ![]() . Then, we define the nonlinear function “f”. To compute the gradient, we use the function “jacobian()”. The input of this function is the symbolic variable (vector) for computing the Jacobian matrix. The Jacobian of a scalar function is the gradient vector. The function “jacobian()” returns a row vector. That is why we need to transpose the result to obtain the gradient vector.
. Then, we define the nonlinear function “f”. To compute the gradient, we use the function “jacobian()”. The input of this function is the symbolic variable (vector) for computing the Jacobian matrix. The Jacobian of a scalar function is the gradient vector. The function “jacobian()” returns a row vector. That is why we need to transpose the result to obtain the gradient vector.
Next, we create a Python function that will return the numerical value of the gradient for the given numerical value of the symbolic vector “x”. The following Python script is used to achieve this task
gradientFunction=lambdify(x,g)
xValue=np.array([[10],[10]])
gradientNumericalValue=gradientFunction(xValue)The function “lambidfy()” is used to convert symbolic expressions into Python functions. The first input argument is the symbolic variable (vector) and the second input argument is the symbolic expression. The “lambdify” function returns the Python function that can be used for computing the numerical value of the symbolic expression. We call this function by passing the numerical value of the symbolic vector.
Next, let us consider the second test case. Consider the following function
(9) ![]()
The gradient is given by
(10) 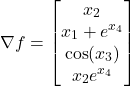
The following Python script is used to compute the gradient of the function (9).
# -*- coding: utf-8 -*-
"""
Computation of Symbolic Gradients in Python and
Automatic Generation of Python Functions for Gradients
"""
import numpy as np
from sympy import *
init_printing()
# symbolic state vector
x = MatrixSymbol('x',4,1)
# nonlinear function
f=Matrix([x[0]*x[1]+sin(x[2])+x[1]*E**(x[3])])
# compute the gradient
g=f.jacobian(x)
# compute the transpose
g=g.transpose()
gradientFunction=lambdify(x,g)
xValue=np.array([[1],[1],[2],[3]])
gradientNumericalValue=gradientFunction(xValue)