In this reinforcement learning tutorial, we explain the basics of the Monte Carlo method for learning state-value functions. Particularly, we explain the first visit method. We provide a Python implementation of the Monte Carlo method and we use the Frozen Lake OpanAI Gym environment to test the methods. The GitHub page with all the codes is given here.
The YouTube page accompanying this tutorial is given below.
Before reading this tutorial, it is a good idea to go over these tutorials:
- Introduction to State Transition Probabilities, Actions, Episodes, and Rewards with OpenAI Gym Python Library- Reinforcement Learning Tutorial
- Installation and Getting Started with OpenAI Gym and Frozen Lake Environment – Reinforcement Learning Tutorial
- Clear Explanation of the Value Function and Its Bellman Equation – Reinforcement Learning Tutorial
Monte Carlo is a model-free method for learning the state-value function. Under the term “model-free method”, we understand a method that does not require a priori information about the state transition probabilities.
First of all, we need to recall the definition of the state value function:
(1) ![]()
where ![]() is the state,
is the state, ![]() is a state at the time step
is a state at the time step ![]() ,
, ![]() is the weighted return defined as follows
is the weighted return defined as follows
(2) ![]()
where
We can clearly observe that the state value function is a mathematical expectation. Roughly speaking, the expected value can be seen as a value obtained by repeating a random experiment an infinite number of times and calculating an average value of the values observed during each random experiment. That is an average of random variables converge to the expectation as the number of experiment increases.
Motivated by this, the main idea of the Monte Carlo method is to simply run many episodes and observe the corresponding state trajectories and obtained rewards. Then, on the basis of this information, the Monte Carlo method approximates the state value function as an average return (weighted sum of rewards) of the returns observed in random episodes.
Let us illustrate this idea graphically. Consider the Frozen Lake environment shown in Fig. 1 below.
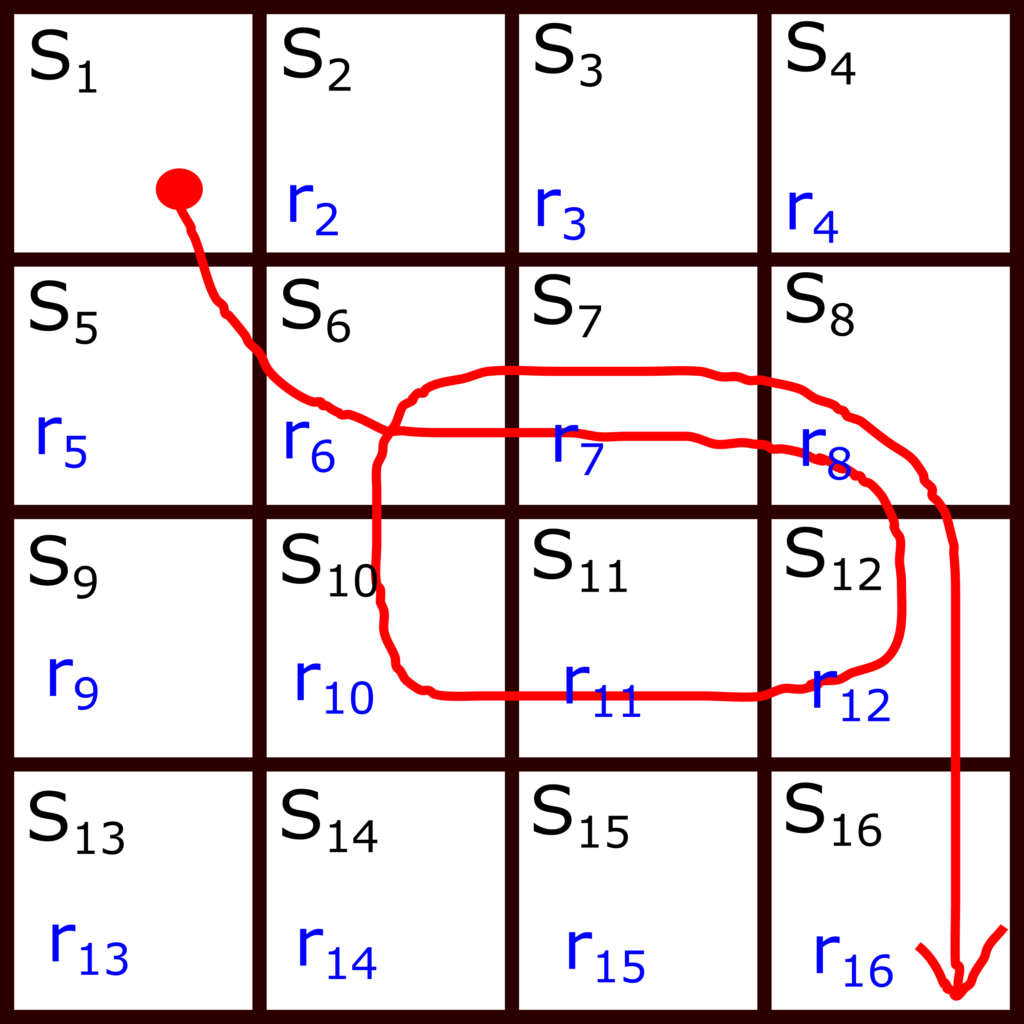
The red line represents states visited during an episode. The start state is ![]() (note that particular states are denoted by the lower case letters). Then end state is the state
(note that particular states are denoted by the lower case letters). Then end state is the state ![]() . This is a terminal state The state trajectory can be represented as
. This is a terminal state The state trajectory can be represented as
(3) ![]()
Note here that with capital letters ![]() , we denote states in a time sequence, where the index
, we denote states in a time sequence, where the index ![]() is the time step.
is the time step.
Each occurrence of the state ![]() in an episode is called a visit. The obtained rewards in the sequence are
in an episode is called a visit. The obtained rewards in the sequence are
(4) ![]()
Let us for a moment assume that the discount rate is ![]() . Since we only have a single episode, the average return for every state will be equal to the return obtained at this single episode. For example, on the basis of only this single episode, we obtain the following estimates of the state value functions by using the Monte Carlo method. The state
. Since we only have a single episode, the average return for every state will be equal to the return obtained at this single episode. For example, on the basis of only this single episode, we obtain the following estimates of the state value functions by using the Monte Carlo method. The state ![]() is the state at the position
is the state at the position ![]() in the time sequence. Consequencely, we have
in the time sequence. Consequencely, we have
(5) ![]()
On the other hand, let us focus on the state ![]() and let us estimate its state value function. This state is visited twice in the sequence, at the time step
and let us estimate its state value function. This state is visited twice in the sequence, at the time step ![]() , that is
, that is ![]() , and at the time step
, and at the time step ![]() , that is
, that is ![]() . The main question is what time instant or what visit of
. The main question is what time instant or what visit of ![]() should be taken into account when computing the return? In the first visit Monte Carlo method, we compute the return starting from the first visit of the state in the sequence. That is, we count the return starting from the time step
should be taken into account when computing the return? In the first visit Monte Carlo method, we compute the return starting from the first visit of the state in the sequence. That is, we count the return starting from the time step ![]() . When we reach
. When we reach ![]() again later in the sequence (at the time instant
again later in the sequence (at the time instant ![]() ), we also count again the reward obtained by visiting the state
), we also count again the reward obtained by visiting the state ![]() for the second time. That is the main idea of the first visit method. Consequently, the state value function at
for the second time. That is the main idea of the first visit method. Consequently, the state value function at ![]() is
is
(6) ![]()
Note here that ![]() is not included in the sum, due to the definition of the state value function (2). That is, for the state at the time step
is not included in the sum, due to the definition of the state value function (2). That is, for the state at the time step ![]() , the sum of rewards starts at
, the sum of rewards starts at ![]() .
.
In the second episode, we observe the rewards and compute the return from every state in the sequence by using a similar strategy. We also count the number of first visits to the particular state. Then, we add these returns to the corresponding returns from the first episode and divide the result by two if the state is visited in this episode. We repeat this process. Generally speaking, if we have N episodes, for every state, we sum the returns in every episode and obtain a total sum of returns. Then we divide this sum of returns by the number of times a particular state was visited for the first time during these N episodes. The result will give us an estimate of the state value function for the particular state. Consider the three episodes shown in the figure below.
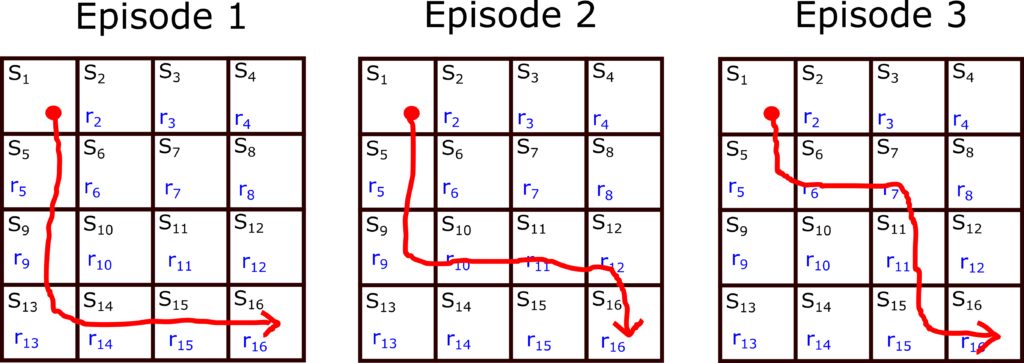
Let us first estimate the value function at the state ![]() . The returns from the state
. The returns from the state ![]() for these three episodes is
for these three episodes is
(7) 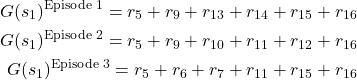
Since the state ![]() is visited 3 times, we have
is visited 3 times, we have
(8) ![]()
Next, let us estimate the state value function at the state ![]() . The state
. The state ![]() is visited in Episode 1 and Episode 2. However, it is not visited in Episode 3. Consequently, since the state
is visited in Episode 1 and Episode 2. However, it is not visited in Episode 3. Consequently, since the state ![]() is visited two times, we have
is visited two times, we have
(9) 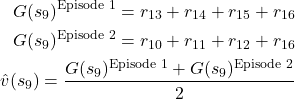
The structure of the Python code should roughly be like this
- Create a for loop that will in every loop simulate an episode. Create vectors that store total returns and the total number of visits for every state during simulated episodes.
- In every episode simulation, that is every iteration of the loop, compute the return from every visited state.
- In every iteration of the loop, update the vectors that store the total return and the total number of visits for every particular state.
- After the loop is completed, divide every entry of the vector storing total returns by the number of visits of a particular state.
The GitHub page with all the codes is given here.
The function that implements the first visit Monte Carlo method is given below.
def MonteCarloLearnStateValueFunction(env,stateNumber,numberOfEpisodes,discountRate):
import numpy as np
# sum of returns for every state
sumReturnForEveryState=np.zeros(stateNumber)
# number of visits of every state
numberVisitsForEveryState=np.zeros(stateNumber)
# estimate of the state value function vector
valueFunctionEstimate=np.zeros(stateNumber)
###########################################################################
# START - episode simulation
###########################################################################
for indexEpisode in range(numberOfEpisodes):
# this list stores visited states in the current episode
visitedStatesInEpisode=[]
# this list stores the return in every visited state in the current episode
rewardInVisitedState=[]
(currentState,prob)=env.reset()
visitedStatesInEpisode.append(currentState)
print("Simulating episode {}".format(indexEpisode))
###########################################################################
# START - single episode simulation
###########################################################################
# here we randomly generate actions and step according to these actions
# when the terminal state is reached, this loop breaks
while True:
# select a random action
randomAction= env.action_space.sample()
# explanation of "env.action_space.sample()"
# Accepts an action and returns either a tuple (observation, reward, terminated, truncated, info)
# https://www.gymlibrary.dev/api/core/#gym.Env.step
# format of returnValue is (observation,reward, terminated, truncated, info)
# observation (object) - observed state
# reward (float) - reward that is the result of taking the action
# terminated (bool) - is it a terminal state
# truncated (bool) - it is not important in our case
# info (dictionary) - in our case transition probability
# env.render()
# here we step and return the state, reward, and boolean denoting if the state is a terminal state
(currentState, currentReward, terminalState,_,_) = env.step(randomAction)
# append the reward
rewardInVisitedState.append(currentReward)
# if the current state is NOT terminal state
if not terminalState:
visitedStatesInEpisode.append(currentState)
# if the current state IS terminal state
else:
break
# explanation of IF-ELSE:
# let us say that a state sequence is
# s0, s4, s8, s9, s10, s14, s15
# the vector visitedStatesInEpisode is then
# visitedStatesInEpisode=[0,4,8,10,14]
# note that s15 is the terminal state and this state is not included in the list
# the return vector is then
# rewardInVisitedState=[R4,R8,R10,R14,R15]
# R4 is the first entry, meaning that this is the reward going
# from state s0 to s4. That is, the rewards correspond to the reward
# obtained in the destination state
###########################################################################
# END - single episode simulation
###########################################################################
# how many states we visited in an episode
numberOfVisitedStates=len(visitedStatesInEpisode)
# this is Gt=R_{t+1}+\gamma R_{t+2} + \gamma^2 R_{t+3} + ...
Gt=0
# we compute this quantity by using a reverse "range"
# below, "range" starts from len-1 until second argument +1, that is until 0
# with the step that is equal to the third argument, that is, equal to -1
# here we do everything backwards since it is easier and faster
# if we go in the forward direction, we would have to
# compute the total return for every state, and this will be less efficient
for indexCurrentState in range(numberOfVisitedStates-1,-1,-1):
stateTmp=visitedStatesInEpisode[indexCurrentState]
returnTmp=rewardInVisitedState[indexCurrentState]
# this is an elegant way of summing the returns backwards
Gt=discountRate*Gt+returnTmp
# below is the first visit implementation
# here we say that if visitedStatesInEpisode[indexCurrentState] is
# visited for the first time, then we only count that visit
# here also note that the notation a[0:3], includes a[0],a[1],a[2] and it does NOT include a[3]
if stateTmp not in visitedStatesInEpisode[0:indexCurrentState]:
# note that this state is visited in the episode
numberVisitsForEveryState[stateTmp]=numberVisitsForEveryState[stateTmp]+1
# add the sum for that state to the total sum for that state
sumReturnForEveryState[stateTmp]=sumReturnForEveryState[stateTmp]+Gt
###########################################################################
# END - episode simulation
###########################################################################
# finally we need to compute the final estimate of the state value function vector
for indexSum in range(stateNumber):
if numberVisitsForEveryState[indexSum] !=0:
valueFunctionEstimate[indexSum]=sumReturnForEveryState[indexSum]/numberVisitsForEveryState[indexSum]
return valueFunctionEstimate
In the sequel, we explain this code. The following two vectors
# sum of returns for every state
sumReturnForEveryState=np.zeros(stateNumber)
# number of visits of every state
numberVisitsForEveryState=np.zeros(stateNumber)
Are used to store the sum of episode returns for every state, and the sum of first visits of every state. These vectors are updated after every episode is simulated. The code lines 31 to 59 are used to simulate an episode. We generate a random action (code line 34), and we observe the destination state and the reward obtained by stepping to this state (code line 48). Note that the function on the code line 48 also returns a boolean variable denoting if the destination state is terminal or not (variable “terminalState”). The code line 51 is used to append the obtained reward. The code lines 54-58 are used to append the state sequence (stored in the vector “currentState”). At the end of this section we will have two lists/vectors. The vector “visitedStatesInEpisode” will contain a sequence of visited states and the vector “rewardInVisitedState” will consist of obtained rewards. For example, let us say that the visited state sequence is ![]() (note that OpenAI Gym counts the states starting from 0). Then, visitedStatesInEpisode=[0,4,8,10,14]. Note that the terminal state
(note that OpenAI Gym counts the states starting from 0). Then, visitedStatesInEpisode=[0,4,8,10,14]. Note that the terminal state ![]() is not included in the list.
is not included in the list.
The code lines 78 to 106 are used to compute the return and to count the number of visits. The for loop in the code line 89 iterates through the entries of visitedStatesInEpisode backwards. This is done in order to simplify the computation of the return for every state in this sequence. Namely, we can represent the return as follows:
(10) ![]()
We can represent this summation backward as follows
(11) 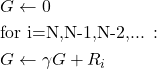
where ![]() is the obtained reward at the time step
is the obtained reward at the time step ![]() . This is actually implemented in the code line 96. The rest of the code is self-explanatory.
. This is actually implemented in the code line 96. The rest of the code is self-explanatory.
When developing a new method it is always a good idea to compare the method with the existing approaches. In this way we can evaluate the method’s accuracy and performance. We compare the first visit Monte Carlo method, with an iterative policy evaluation method for computing the state value function. The function below that implements the iterative policy evaluation algorithm is explained in this post, and for completeness of this tutorial is given below.
##################
# this function computes the state value function by using the iterative policy evaluation algorithm
##################
# inputs:
##################
# env - environment
# valueFunctionVector - initial state value function vector
# policy - policy to be evaluated - this is a matrix with the dimensions (number of states)x(number of actions)
# - p,q entry of this matrix is the probability of selection action q in state p
# discountRate - discount rate
# maxNumberOfIterations - max number of iterations of the iterative policy evaluation algorithm
# convergenceTolerance - convergence tolerance of the iterative policy evaluation algorithm
##################
# outputs:
##################
# valueFunctionVector - final value of the state value function vector
##################
def evaluatePolicy(env,valueFunctionVector,policy,discountRate,maxNumberOfIterations,convergenceTolerance):
import numpy as np
convergenceTrack=[]
for iterations in range(maxNumberOfIterations):
convergenceTrack.append(np.linalg.norm(valueFunctionVector,2))
valueFunctionVectorNextIteration=np.zeros(env.observation_space.n)
for state in env.P:
outerSum=0
for action in env.P[state]:
innerSum=0
for probability, nextState, reward, isTerminalState in env.P[state][action]:
#print(probability, nextState, reward, isTerminalState)
innerSum=innerSum+ probability*(reward+discountRate*valueFunctionVector[nextState])
outerSum=outerSum+policy[state,action]*innerSum
valueFunctionVectorNextIteration[state]=outerSum
if(np.max(np.abs(valueFunctionVectorNextIteration-valueFunctionVector))<convergenceTolerance):
valueFunctionVector=valueFunctionVectorNextIteration
print('Iterative policy evaluation algorithm converged!')
break
valueFunctionVector=valueFunctionVectorNextIteration
return valueFunctionVector
##################
Also, we will need the code below that is used to visualize the results.
##################
# this function visualizes and saves the state value function
##################
# inputs:
##################
# valueFunction - state value function vector to plot
# reshapeDim - reshape dimension
# fileNameToSave - file name to save the figure
def grid_print(valueFunction,reshapeDim,fileNameToSave):
import seaborn as sns
import matplotlib.pyplot as plt
ax = sns.heatmap(valueFunction.reshape(reshapeDim,reshapeDim),
annot=True, square=True,
cbar=False, cmap='Blues',
xticklabels=False, yticklabels=False)
plt.savefig(fileNameToSave,dpi=600)
plt.show()
##################
Below is the driver code that demonstrates how to use the developed functions:
# -*- coding: utf-8 -*-
"""
Reinforcement Learning Tutorial:
First Visit Monte Carlo Method for Learning the state value function
for a given policy
Tested on the Frozen Lake OpenAI Gym environment.
Author: Aleksandar Haber
Date: December 2022
This is the driver code that coles functions from "functions.py"
"""
import gym
import numpy as np
from functions import MonteCarloLearnStateValueFunction
from functions import evaluatePolicy
from functions import grid_print
# create an environment
# note here that we create only a single hole to makes sure that we do not need
# a large number of simulations
# generate a custom Frozen Lake environment
desc=["SFFF", "FFFF", "FFFF", "HFFG"]
# here we render the environment- use this only for illustration purposes
# env=gym.make('FrozenLake-v1', desc=desc, map_name="4x4", is_slippery=True,render_mode="human")
# uncomment this and comment the previous line in the case of a large number of simulations
env=gym.make('FrozenLake-v1', desc=desc, map_name="4x4", is_slippery=True)
# number of states in the environment
stateNumber=env.observation_space.n
# number of simulation episodes
numberOfEpisodes=10000
# discount rate
discountRate=1
# estimate the state value function by using the Monte Carlo method
estimatedValuesMonteCarlo=MonteCarloLearnStateValueFunction(env,stateNumber=stateNumber,numberOfEpisodes=numberOfEpisodes,discountRate=discountRate)
# for comparison compute the state value function vector by using the iterative policy
# evaluation algorithm
# select an initial policy
# initial policy starts with a completely random policy
# that is, in every state, there is an equal probability of choosing a particular action
initialPolicy=(1/4)*np.ones((16,4))
# initialize the value function vector
valueFunctionVectorInitial=np.zeros(env.observation_space.n)
# maximum number of iterations of the iterative policy evaluation algorithm
maxNumberOfIterationsOfIterativePolicyEvaluation=1000
# convergence tolerance
convergenceToleranceIterativePolicyEvaluation=10**(-6)
# the iterative policy evaluation algorithm
valueFunctionIterativePolicyEvaluation=evaluatePolicy(env,valueFunctionVectorInitial,initialPolicy,1,maxNumberOfIterationsOfIterativePolicyEvaluation,convergenceToleranceIterativePolicyEvaluation)
# plot the result
grid_print(valueFunctionIterativePolicyEvaluation,reshapeDim=4,fileNameToSave='iterativePolicyEvaluationEstimated.png')
# plot the result
grid_print(estimatedValuesMonteCarlo,reshapeDim=4,fileNameToSave='monteCarloEstimated.png')
First, we import the necessary libraries and the developed functions. Then we create a custom Frozen Lake environment with only a single hole. This is done in order to have a relatively small number of necessary episodes to evaluate the state value functions. If we have too many holes, then most of the times we will never reach the goal terminal state since we will stuck in the holes most of the times. Then, on the code line 45 we compute the state value function vector by using the Monte Carlo method. Then, for comparison we use the iterative policy evaluation algorithm to compute the state value function vector. We select a random policy in the code line 54, and on the code line 64 we call the function that computes the state value function. Finally, we plot the results on the grids that are shown below.

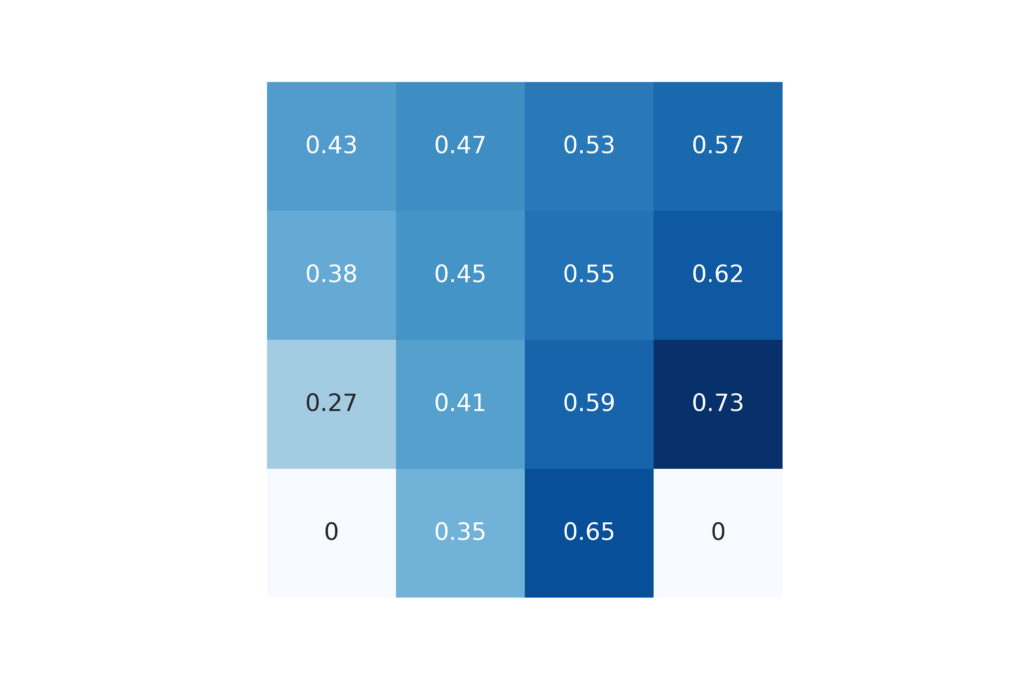
We can see that the results present in the figures 2 and 3 are identical up to 2 decimal spaces. This implies that we have accurately designed and implemented the Monte Carlo method for approximating the state value functions.