1. Introduction
In this post and in the accompanying YouTube tutorial, we provide explanations of transient response specifications: peak time, settling time, rise time, overshoot, and percent overshoot. The YouTube video accompanying this post is given below.
The values of peak time, settling time, rise time, and percent overshoot are very important for control design. We often specify the desired system behavior in terms of the values of these parameters of the transient response. Then, on the basis of the desired values of these parameters, we design the control system. Also, for second-order systems, we can relate damping ratio, natural frequency, bandwidth, and some other properties of the dynamical systems with the values of peak time, settling time, rise time, and percent overshoot.
In this post, we formally define the peak time, settling time, rise time, and percent overshoot and we provide graphical explanations of these important parameters.
How to Cite This Document:
“Transient Response Specifications: Peak time, Settling time, Rise Time, Overshoot, and Percent Overshoot”. Technical Report, Number 4, Aleksandar Haber, (2023), Publisher: www.aleksandarhaber.com, Link: https://aleksandarhaber.com/transient-response-specifications-peak-time-settling-time-rise-time-and-percent-overshoot/
Copyright Notices and NOT to Be Used for AI Notice
COPYRIGHT NOTICE: THE TEXT, PHOTOS, AND CODES POSTED ON THIS WEBSITE AND ON THIS WEBPAGE ARE THE OWNERSHIP, INTELLECTUAL PROPERTY, AND COPYRIGHTED BY THE AUTHOR: ALEKSANDAR HABER. THE TEXT AND THE CONTENT OF THIS PAGE SHOULD NOT BE PHYSICALLY COPIED, SHOULD NOT BE COPIED ON OTHER WEBSITES, SHOULD NOT BE REPRINTED, SHOULD NOT BE REPOSTED ON OTHER WEBSITES, SHOULD NOT BE USED AS A LECTURE MATERIAL IN UNIVERSITY COURSES, SHOULD NOT BE USED AS LECTURE MATERIAL IN COURSES ORGANIZED BY AND HOSTED ON ONLINE LEARNING PLATFORMS (such as Udemy, Coursera, etc), AND SHOULD NOT BE USED IN COMMERCIAL SETTING. THE TEXT, PHOTOS, AND CODE PRESENTED ON THIS WEBSITE AND WEBPAGE SHOULD NOT BE INCLUDED IN REPORTS, STUDENT PAPERS, SCIENTIFIC PAPERS, OR IN ANY OTHER PRINTED OR A DIGITAL FORM OR A DOCUMENT WITHOUT WRITTEN CONSENT OF THE AUTHOR. A MONEY FEE MIGHT BE REQUIRED TO REPRINT THE MATERIAL POSTED ON THIS WEBSITE: CONTACT THE AUTHOR: ml.mecheng@gmail.com
CODE COPYRIGHT NOTICE AND LICENSE: THE CODE FILES POSTED ON THIS WEBSITE ARE NOT FREE SOFTWARE AND CODE. IF YOU WANT TO USE THIS CODE IN THE COMMERCIAL SETTING OR ACADEMIC SETTING, THAT IS, IF YOU WORK FOR A COMPANY OR IF YOU ARE AN INDEPENDENT CONSULTANT AND IF YOU WANT TO USE THIS CODE OR IF YOU ARE ACADEMIC RESEARCHER OR STUDENT, THEN WITHOUT MY PERMISSION AND WITHOUT PAYING THE PROPER FEE, YOU ARE NOT ALLOWED TO USE THIS CODE. YOU CAN CONTACT ME AT
ml.mecheng@gmail.com
TO INFORM YOURSELF ABOUT THE LICENSE OPTIONS AND FEES FOR USING THIS CODE. ALSO, IT IS NOT ALLOWED TO (1) MODIFY THIS CODE IN ANY WAY WITHOUT MY PERMISSION. (2) INTEGRATE THIS CODE IN OTHER PROJECTS WITHOUT MY PERMISSION. (3) POST THIS CODE ON ANY PRIVATE OR PUBLIC WEBSITES OR CODE REPOSITORIES. DELIBERATE OR INDELIBERATE VIOLATIONS OF THIS LICENSE WILL INDUCE LEGAL ACTIONS AND LAWSUITS.
NOT TO BE USED FOR AI COPYRIGHT NOTICE: The code and text, as well as all other material on this webpage and the YouTube page, should NOT be used to train an AI algorithm or a large language model, or any type of AI or machine learning algorithm used to recognize, interpret, and draw conclusions from text. Also, it is forbidden to crawl this webpage and to extract information for training an AI algorithm of any sort on the basis of the material presented on this webpage.
Compute the Transient Response in MATLAB
The step response that is shown in the figures below is computed for the following system
(1) ![]()
The step response is computed by using the following MATLAB code
zeta=0.4
wn=2
transferFunction= tf([wn^2],[1 2*zeta*wn wn^2])
[y,time1]=step(transferFunction)
plot(time1,y)
2. Settling time
Settling time, denoted by ![]() is graphically explained in Fig. 1. below. The final or steady-state value of the system response is denoted by
is graphically explained in Fig. 1. below. The final or steady-state value of the system response is denoted by ![]() .
.
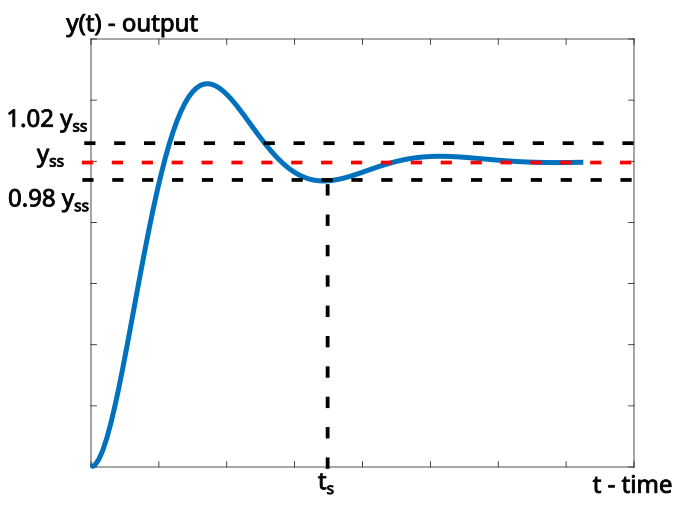
Definition of ![]() settling time: The settling time
settling time: The settling time ![]() is defined as the time required for the transient response to enter and stay within
is defined as the time required for the transient response to enter and stay within ![]() of the steady-state or final value.
of the steady-state or final value.
Here are a few important comments about the settling time. First of all, in a similar manner and spirit to the above definition, we can also define ![]() settling time. Then, obviously, the definition of the settling time implicitly assumes that the system reaches a finite steady state. This implicitly implies that the underlying system is asymptotically stable. As is demonstrated in Fig. 1, we can construct the settling time by first drawing a horizontal line starting from the steady-state value of the response. Then, we offset this line
settling time. Then, obviously, the definition of the settling time implicitly assumes that the system reaches a finite steady state. This implicitly implies that the underlying system is asymptotically stable. As is demonstrated in Fig. 1, we can construct the settling time by first drawing a horizontal line starting from the steady-state value of the response. Then, we offset this line ![]() to obtain an interval or a tunnel. Then we search for an intersection of the system response with the
to obtain an interval or a tunnel. Then we search for an intersection of the system response with the ![]() horizontal line such that the response enters and never leaves the tunnel after the intersection point. The time corresponding to the intersection point is our settling time.
horizontal line such that the response enters and never leaves the tunnel after the intersection point. The time corresponding to the intersection point is our settling time.
Finally, the settling time, as well as other transient response parameters defined in this post can also be defined for not only second-order systems but for systems of arbitrary orders.
3. Peak Time
The peak time is another important characteristic of the transient system response. It is usually defined as follows:
Definition of the peak time: The peak time, denoted by ![]() is defined as the time required for the system to reach the maximum overshoot.
is defined as the time required for the system to reach the maximum overshoot.
The peak time is illustrated in Fig. 2. below.
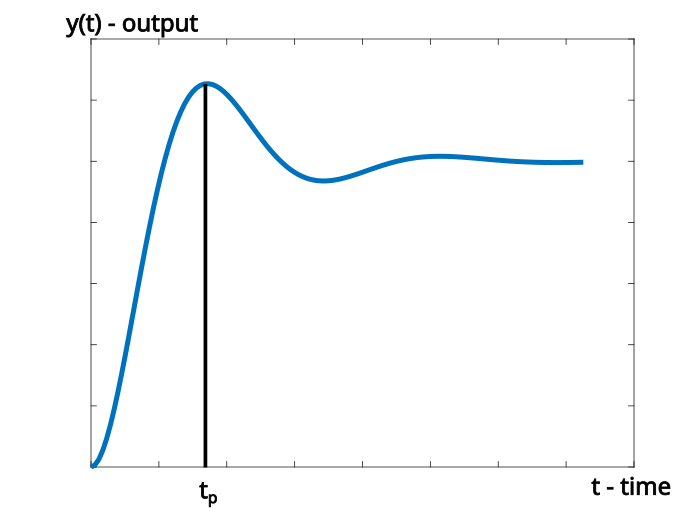
Figure 2: Graphical explanation of the peak time of the transient response.
4. Rise Time
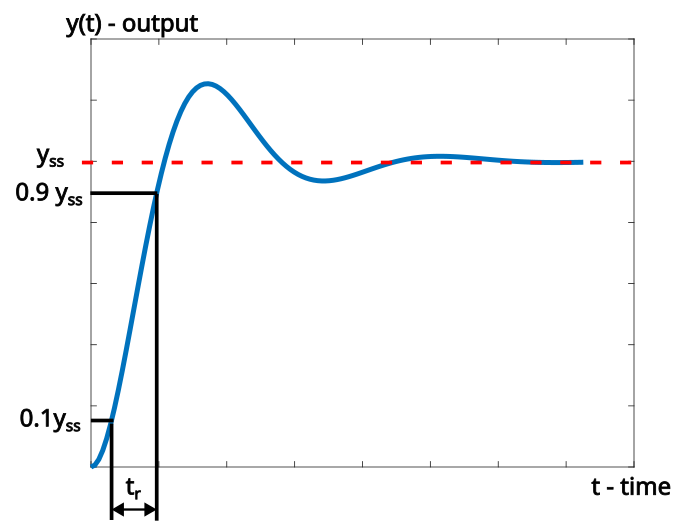
Definition of the rise time: The rise time is the time required for the system response to go from ![]() to
to ![]() of its final or steady-state value.
of its final or steady-state value.
The rise time is explained in Fig. 3 below. The final or steady-state value of the system response is denoted by ![]() .
. ![]() and
and ![]() of the final values are denoted by
of the final values are denoted by ![]() and
and ![]() , respectively.
, respectively.
5. Overshoot and percentage overshoot
The maximum overshoot can be defined as follows:
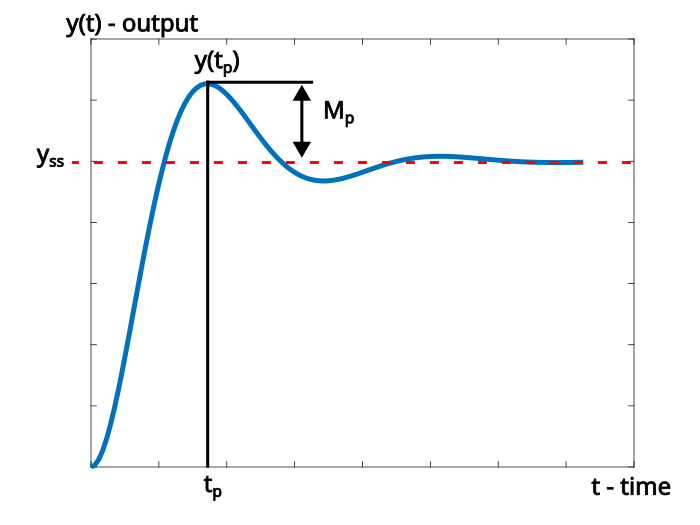
Definition of the (maximum) overshoot: The (maximum) overshoot, denoted by ![]() is defined by
is defined by
(2) ![]()
where ![]() is the peak time for which the step response achieves a maximum value, and
is the peak time for which the step response achieves a maximum value, and ![]() is the final or the steady value of the step response. The (maximum) overshoot is illustrated in Fig. 4 below.
is the final or the steady value of the step response. The (maximum) overshoot is illustrated in Fig. 4 below.
Definition of the (maximum) percentage overshoot: The (maximum) percentage overshoot, denoted by ![]() is defined by
is defined by
(3) ![]()