Torsion – Design Problems – Fusion of Engineering, Control, Coding, Machine Learning, and Science

Problem 1. Consider a circular shaft with a diameter of $d$ made of steel (A53 Seamless and Welded Standard Steel Pipe – Grade B). This shaft has to transfer torque of $T=10^{5}$ $[Nm]$ . Design the shaft diameter such that the shaft can safely withstand this load.

Solution: To solve this problem, we first need to read the value of the critical stress for the given material. In a table given here, we see that the yield strength is $\sigma_{Y}=241 [MPa]$ . However, this is the critical value of normal stress. We have learned that when a circular shaft is subject to external torques, shear stresses will appear in the cross-section normal to the shaft’s axis. Consequently, we need the value of the shear yield stress. An engineering rule of thumb is to approximate this value by $\tau_{Y}\in [0.5\sigma_{Y}, 0.75\sigma_{Y}]$ , see, for example, this page and this page.

In this example, we will approximate the shear yield stress by

(1) $\begin{align*}\tau_{Y}=0.75\sigma_{Y}\end{align*}$

The next step, is to use the design equation:

(2) $\begin{align*}\tau_{\text{max}}=\frac{\tau_{Y}}{S}\end{align*}$

where $S > 1$ is the factor of safety that we need to select, and $\tau_{ \text{max} }$ is the maximal shear stress. The design equation (2) states that the maximal stress created by the external torque should be smaller than the critical value of the stress that causes plastic deformations. That is, we need to select the shaft diameter such that the maximal stress is smaller than the shear yield strength. Usually, the factor of safety is in the interval $S\in [2,5]$ , and it is a user choice.

The shear stress distribution created by external torsional forces is shown in the figure below.

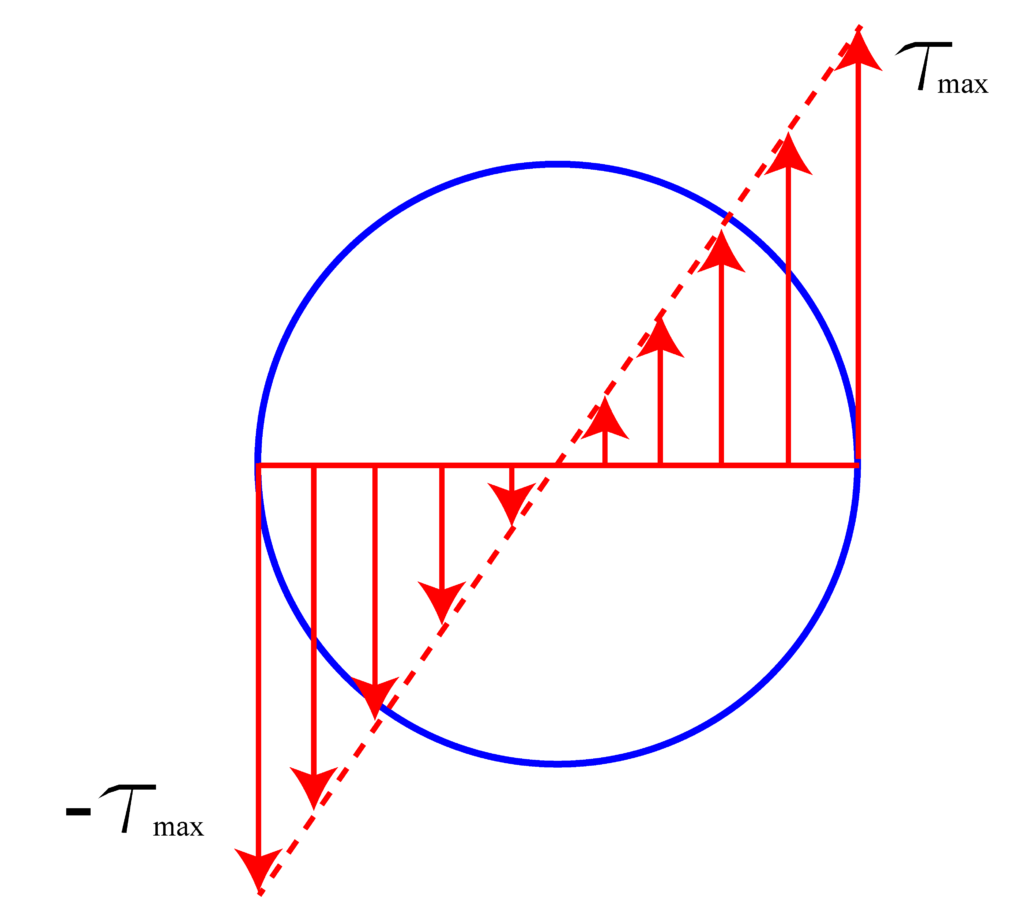
Figure 1: Shear stress distribution caused by external torsional forces.

We have learned that maximal stress value is determined by

(3) $\begin{align*}\tau_{\text{max}}=\frac{T}{\frac{J}{c}}\end{align*}$

where $J$ is the polar moment of inertia and $c$ is the maximal distance of the cross-section points from the center. For the circular cross-section, we have

(4) $\begin{align*}J=\frac{1}{2}\pi R^{4}, \;\;\; c=R\end{align*}$

We have $R=\frac{d}{2}$ , and by using this value, we have

(5) $\begin{align*}\frac{J}{c}= \frac{ \frac{1}{2}\pi (\frac{d}{2})^{4} }{\frac{d}{2}}=\frac{\pi d^{3}}{16}\end{align*}$

By substituting (5) in (3), we obtain

(6) $\begin{align*} \tau_{\text{max}}=\frac{T}{ \frac{\pi d^{3}}{16} } =\frac{16 T}{ \pi d^{3} }\end{align*}$

Next, we substitute (6) in (2), we obtain

(7) $\begin{align*} \frac{16 T}{ \pi d^{3} } =\frac{\tau_{Y}}{S}\end{align*}$

From the last equation, we have

(8) $\begin{align*}d=\Big(\frac{16 \cdot T \cdot S}{\pi\cdot \tau_{Y}} \Big)^{\frac{1}{3}}\end{align*}$

By substituting the values for the Torque, factor of safety, and shear yield stress in the last equation, we can easily calculate the shaft diameter $d$ .

admin

You might also like

COMSOL Tutorial: Thin-Plate Deformation

Starting With Multi-class Classification in Scikit-learn and Python (Using Support Vector Machines)

Homework Assignment 4