This is the second part of the tutorial on Euler angles and rigid kinematics. These tutorials are important for robotics and aerospace engineers. In this tutorial, we provide a clear explanation of Yaw, Pitch, and Roll Euler angles. We focus on the so-called 3-2-1 Yaw, Pitch, and Roll Euler angles. In the first part of this tutorial which can be found here, we focused on the classical Z-Z’-Z” Euler angles. The YouTube tutorial accompanying this post is given below.
Graphical Interpretation and Geometry of Yaw-Pitch-Roll Euler Angles and Rotations
The yaw-pitch-roll Euler angles are animated in the video shown below. Before continuing to read the rest of this tutorial, first, watch the video given below in order to better understand the geometry of yaw-pitch-roll Euler angles.
The yaw-pitch-roll angles and induced rotations are graphically explained in the figure below.
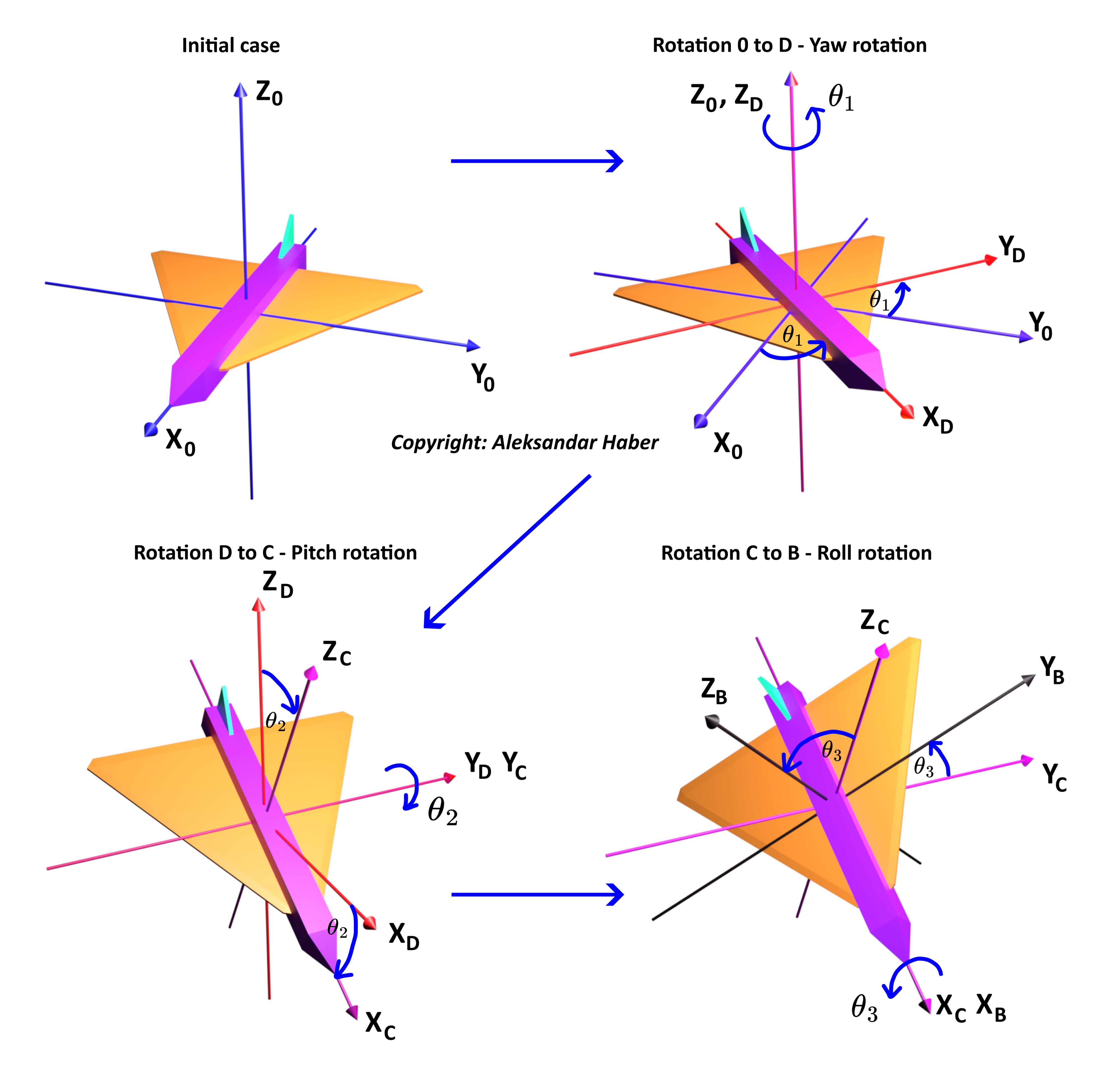
The coordinate system ![]() with the coordinate axes
with the coordinate axes ![]() is an inertial (fixed) coordinate system.
is an inertial (fixed) coordinate system.
We have three rotations
- Rotation around the
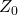 axis for the angle of
axis for the angle of 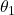 . This is the yaw rotation. This rotation defines the coordinate system
. This is the yaw rotation. This rotation defines the coordinate system 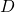 with the coordinate axes
with the coordinate axes 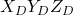 .
. - Rotation around the
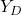 axis for the angle of
axis for the angle of 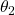 . This is the pitch rotation. This rotation defines the coordinate system
. This is the pitch rotation. This rotation defines the coordinate system 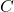 with the coordinate axes
with the coordinate axes 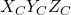 .
. - Rotation around the
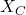 axis for the angle of
axis for the angle of 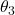 . This is the roll rotation. This rotation defines the coordinate system
. This is the roll rotation. This rotation defines the coordinate system  with the coordinate axes
with the coordinate axes 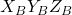 .
.
In robotics and aerospace engineering, coordinate systems are also called frames. The coordinate system ![]() is also called the body frame. This is the frame that is rigidly attached to the body of the object and it rotates with the object. The directions of its axes are usually along the lines of symmetry or along the so-called principal axes or principal axes of inertia. We can also interpret the above rotations as follows. The body frame is rigidly attached to the body. After the yaw rotation, the body frame coincides with the frame
is also called the body frame. This is the frame that is rigidly attached to the body of the object and it rotates with the object. The directions of its axes are usually along the lines of symmetry or along the so-called principal axes or principal axes of inertia. We can also interpret the above rotations as follows. The body frame is rigidly attached to the body. After the yaw rotation, the body frame coincides with the frame ![]() . After the pitch rotation, the body frame coincides with the coordinate system
. After the pitch rotation, the body frame coincides with the coordinate system ![]() . Finally, after the roll rotation, the coordinate system
. Finally, after the roll rotation, the coordinate system ![]() is in its final position.
is in its final position.
The angles ![]() ,
, ![]() , and
, and ![]() are the yaw-pitch-roll Euler angles. The angle
are the yaw-pitch-roll Euler angles. The angle ![]() is called the yaw angle. The angle
is called the yaw angle. The angle ![]() is the pitch angle. The angle
is the pitch angle. The angle ![]() is the roll angle.
is the roll angle.
Next, let us introduce the following notation. Let ![]() be a vector. Then, the notation
be a vector. Then, the notation ![]() is the notation for the vector
is the notation for the vector ![]() expressed in the coordinate system
expressed in the coordinate system ![]() with the following projections in the coordinate system
with the following projections in the coordinate system ![]() :
:
(1) 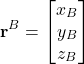
An equivalent notation is valid for ![]() ,
, ![]() , and
, and ![]() , that is
, that is
(2) 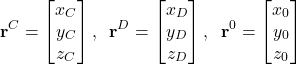
The figure below illustrates the vector ![]() in the coordinate system
in the coordinate system ![]() .
.
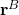 with the coordinate system
with the coordinate system  .
.This vector has the following projections in the coordinate system ![]() .
.
(3) 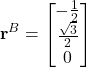
We consider the following important problem.
We are given the angles of rotation ![]() and
and ![]() and we are given the projections of the vector
and we are given the projections of the vector ![]() in the coordinate system
in the coordinate system ![]() . That is, we are given
. That is, we are given ![]() . We want to determine the coordinates of the vector
. We want to determine the coordinates of the vector ![]() in the coordinate system
in the coordinate system ![]() , that is, we want to determine the projections of
, that is, we want to determine the projections of ![]() .
.
This problem is graphically illustrated in the figure below. We want to find the projections of the vector ![]() in the coordinate system
in the coordinate system ![]() .
.
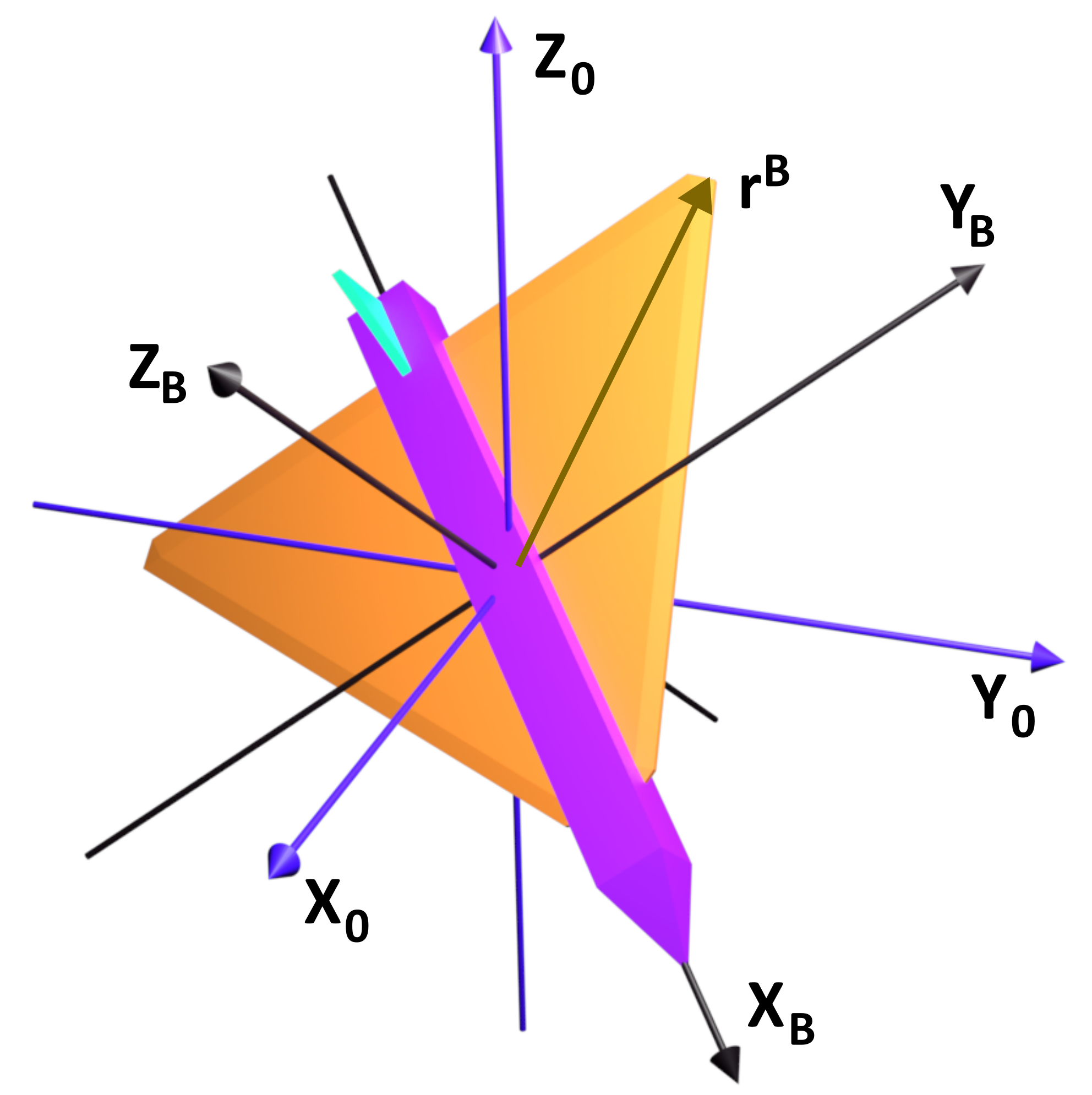
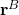 with the coordinate systems
with the coordinate systems  and
and 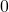 .
.To solve this problem, we need to use rotation matrices that are explained in our previous tutorials, given here, here, and here. Let us now look at the rotation ![]() shown in Fig. 1. By using the rotation matrices, we can represent the vector
shown in Fig. 1. By using the rotation matrices, we can represent the vector ![]() in the coordinate system
in the coordinate system ![]() by using this transformation
by using this transformation
(4) ![]()
where ![]() is the rotation matrix. The matrix
is the rotation matrix. The matrix ![]() is also denoted by
is also denoted by ![]() . The notation
. The notation ![]() is the classical notation for the rotation matrix that transforms the coordinate system
is the classical notation for the rotation matrix that transforms the coordinate system ![]() into the coordinate system
into the coordinate system ![]() . Since the rotation is performed around the
. Since the rotation is performed around the ![]() axis, according to our previous tutorial on rotation matrices, which can be found here, the rotation matrix has the following form
axis, according to our previous tutorial on rotation matrices, which can be found here, the rotation matrix has the following form
(5) 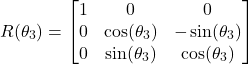
Next, by using the same logic, from Fig. 1. above, we obtain
(6) ![]()
where ![]() (or equivalently,
(or equivalently, ![]() ) is the rotation matrix transforming the coordinate system
) is the rotation matrix transforming the coordinate system ![]() into the coordinate system
into the coordinate system ![]() . Since the rotation is performed with respect to the axis
. Since the rotation is performed with respect to the axis ![]() , according to our previous tutorial, which can be found here, the rotation matrix
, according to our previous tutorial, which can be found here, the rotation matrix ![]() is defined by
is defined by
(7) 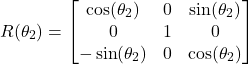
Finally, by using the same logic, from Fig. 1 above, we have
(8) ![]()
where ![]() is the representation of the vector
is the representation of the vector ![]() in the coordinate system
in the coordinate system ![]() , and
, and ![]() (or equivalently,
(or equivalently, ![]() ) is the rotation matrix transforming the coordinate system
) is the rotation matrix transforming the coordinate system ![]() into the coordinate system
into the coordinate system ![]() . Since the rotation is performed with respect to the axis
. Since the rotation is performed with respect to the axis ![]() , according to our previous tutorial, which can be found here, the rotation matrix
, according to our previous tutorial, which can be found here, the rotation matrix ![]() is defined by
is defined by
(9) 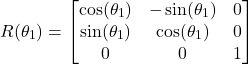
By combining the equations (4), (6), and (8) we obtain
(10) ![]()
The last expression can be written compactly as follows
(11) ![]()
where
(12) ![]()
The matrix ![]() is the direction cosine matrix. It transforms the projections of vectors from the coordinate system
is the direction cosine matrix. It transforms the projections of vectors from the coordinate system ![]() to projections of vectors in the coordinate system
to projections of vectors in the coordinate system ![]() . In our previous tutorial, which can be found here, we explained the main properties of the direction cosine matrix. Next, let us find the explicit form of the matrix
. In our previous tutorial, which can be found here, we explained the main properties of the direction cosine matrix. Next, let us find the explicit form of the matrix ![]() :
:
(13) 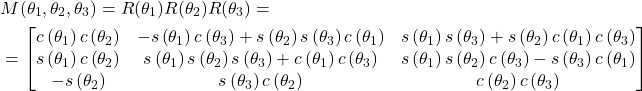
where ![]() is the short notation for
is the short notation for ![]() and
and ![]() is the short notation for
is the short notation for ![]() .
.
The equation (11) solves our problem. The Python code given below is used to compute the direction cosine matrix ![]() :
:
from sympy import *
import numpy as np
init_printing()
theta1=symbols('theta1')
theta2=symbols('theta2')
theta3=symbols('theta3')
Rtheta1=Matrix([[cos(theta1) , -sin(theta1) , 0],
[sin(theta1) , cos(theta1), 0],
[0 , 0, 1]
])
Rtheta2=Matrix([ [cos(theta2),0, sin(theta2)],
[0, 1, 0],
[-sin(theta2), 0, cos(theta2)]
])
Rtheta3=Matrix([ [1, 0, 0],
[0 ,cos(theta3),-sin(theta3)],
[0 ,sin(theta3) , cos(theta3) ]
])
# double check that inverses are transposes
simplify(Rtheta1.T*Rtheta1)
simplify(Rtheta2.T*Rtheta2)
simplify(Rtheta3.T*Rtheta3)
# determine the direction cosine matrix
M=Rtheta1*Rtheta2*Rtheta3
# print(M)
# double check the orthogonality
simplify(M.T*M)
simplify(M.T*M -eye(3))
# generate the latex script
print_latex(M)