Euler Rotation Matrices in Python by Using Symbolic Python Toolbox – SymPy – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this robotics and aerospace tutorial, we will learn how to manipulate and perform operations with rotation and direction cosine matrices in Python by using SymPy. SymPy is a symbolic Python toolbox used for symbolic computations. In particular, we will learn how to

Symbolically define rotation matrices in Python.
How to perform symbolic operations on rotation and direction cosine matrices.
How to substitute symbolic values with numerical values such that the rotation matrices can be evaluated.
How to define a function that will return numerical values of the symbolic rotation or direction cosine matrix.

The YouTube tutorial accompanying this post is given below.

In our previous tutorials, we thoroughly explained the concept of rotation matrices. Also, we derived the mathematical expressions for the rotation matrices.

In the tutorial given here, we explained the X-axis rotation matrix. This matrix has the following form
(1) $\begin{align*} R_{X}(\theta) =\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) \\ 0 & \sin(\theta) & \cos(\theta) \end{bmatrix}\end{align*}$
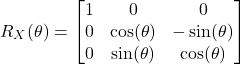
In the tutorial given here, we explained the Y-axis rotation matrix. This matrix has the following form
(2) $\begin{align*} R_{Y}(\theta) = \begin{bmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{bmatrix}\end{align*}$
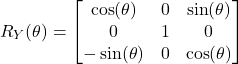
In the tutorial given here, we explained the Z-axis rotation matrix. This matrix has the following form
(3) $\begin{align*} R_{Z}(\theta) =\begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 \\\sin(\theta) & \cos(\theta)& 0 \\ 0 & 0 & 1 \end{bmatrix}\end{align*}$

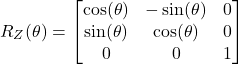
We will use the SymPy toolbox. SymPy is a symbolic Python toolbox used for symbolic computations. First, we import all the functions from the SymPy toolbox.

from sympy import * 
import numpy as np

Next, we call the function “init_printing()” for “nice” printing of symbolic expressions and we define the symbolic angles $\theta_{1}$ , $\theta_{2}$ , and $\theta_{3}$ .

init_printing()

theta1=symbols('theta1')
theta2=symbols('theta2')
theta3=symbols('theta3')

Next, we define the rotation matrices.

Rtheta1=Matrix([[1 , 0 , 0],
                [0 , cos(theta1), -sin(theta1)],
                [0 , sin(theta1), cos(theta1)]
                ])


Rtheta2=Matrix([ [cos(theta2),0, sin(theta2)],
                 [0, 1, 0],
                 [-sin(theta2), 0, cos(theta2)]
                 ])

Rtheta3=Matrix([ [cos(theta3), -sin(theta3), 0],
                 [sin(theta3), cos(theta3), 0],
                 [0, 0, 1]
                 ])

The rotation matrices are orthogonal. This means that

(4) $\begin{align*}I=R^{T}(\theta)\cdot R(\theta)\end{align*}$

where $I$ is the identity matrix. Next, let us double-check that the rotation matrices are orthogonal.

# double check that inverses are transposes 
simplify(Rtheta1.T*Rtheta1)

simplify(Rtheta2.T*Rtheta2)

simplify(Rtheta3.T*Rtheta3)

As a result, we obtained identity matrices which means that we have properly defined the rotation matrices. Next, we define the direction cosine matrix that is equal to the product of the rotation matrices. More about direction cosine matrices can be found in this tutorial and this tutorial. The direction cosine matrix is defined by

(5) $\begin{align*}M(\theta_{1},\theta_{2},\theta_{3})=R(\theta_{1})R(\theta_{2})R(\theta_{3})\end{align*}$

Below is the Python code

# determine the direction cosine matrix
M=Rtheta1*Rtheta2*Rtheta3
# print(M)
# double check the orthogonality
simplify(M.T*M)
simplify(M.T*M -eye(3))

We can generate a Latex source code out of a symbolic expression as follows

# generate the latex script
print_latex(M)

Next, let us learn how to numerically evaluate symbolic rotation matrices in Python. There are at least two approaches.

The first approach is given below.


# Numericaly evaluate the symbolic matrix
theta1Value=np.pi/3
theta2Value=np.pi/6
theta3Value=np.pi/12

M1=M.evalf(subs={theta1:theta1Value,theta2:theta2Value,theta3:theta3Value})
M2=np.array(M1)
# double check
np.matmul(M2,M2.transpose())

First, we define the angles in radians. Then, we use the method “evalf()” to compute the expressions. We specify the names of the symbols and numerical values for every symbol. Finally, we transform the expressions in NumPy arrays, and we double-check the orthogonality.

The second approach is to create lambda functions. This approach is given below.

# let us crate a Python lambda function which will be used 
# compute the numerical values
Mfunction = lambdify([theta1, theta2, theta3], M)

Mfunction(theta1Value,theta2Value,theta3Value)

admin

You might also like

Test 3

Free Fall of an Object (Ball) With Aerodynamic Drag Force

Automatically Compute Jacobians of Vector Functions in Python by Using Symbolic Library