In this tutorial series, we explain what is dead reckoning. We focus on the application of dead reckoning in mobile robotics. We concisely explain the main idea of dead reckoning and we explain how to use a simple approach for solving the dead reckoning problem and for implementing the solution. In the second part of this tutorial given here, we explain how to simulate dead reckoning in Python for a simple model of a mobile robot.
The dead reckoning implementation approach presented in this tutorial is far from optimal, and we can say that it is actually a “naive” approach. However, this naive approach is very useful for understanding the advantages and disadvantages of dead reckoning and learning how to simulate dead reckoning in Python. In the third and fourth parts of this tutorial series, we will present a more optimal approach for solving the dead reckoning problem.
There are a number of definitions and problem formulations of dead reckoning. In this tutorial, under the term “dead reckoning”, we understand the following. Briefly speaking, dead reckoning is a method for calculating (estimating) the position and orientation of a mobile robot at the current time instant by using information about
- The position and orientation of the mobile robot at the previous time instant.
- Measurements of the traveled distance and change of orientation of the mobile robot between the previous and current time instants.
Dead reckoning is probably a centuries-old (if not millennia-old) method used for navigation and location determination by using incremental measurements. It was used for incrementally determining the position of a ship on an open sea. In the first tutorial part presented here, we explain how to use a “naive” approach for dead reckoning in mobile robotics. The idea is to use wheel encoder measurements and gyroscopes to update the location and orientation of the robot. After some time the variance of the estimation error will become very large and this method will not work. This is due to the accumulation and integration of the measurement and approximation errors in every step. That is, the dead reckoning method is useful for short-term localization.
This method should be studied and properly understood before implementing more advanced methods for robotic localization such as nonlinear Kalman filters and particle filters.
The YouTube tutorial accompanying this webpage tutorial is given below.
Kinematic Model of Mobile Robot for Dead Reckoning
Before we mathematically define the process of dead reckoning, we first need to introduce a kinematic model of a mobile robot. This is because the dead reckoning method relies upon simplified kinematics models of mobile robots.
The figure below shows a simple mobile robot with two active wheels and a third passive wheel (castor wheel) that for clarity is not shown in this figure. This is a graphical representation of a differential drive mobile robot explained in our previous tutorial given here. However, the main principle of the dead reckoning method that is explained in this tutorial is applicable to other mobile robotic configurations.
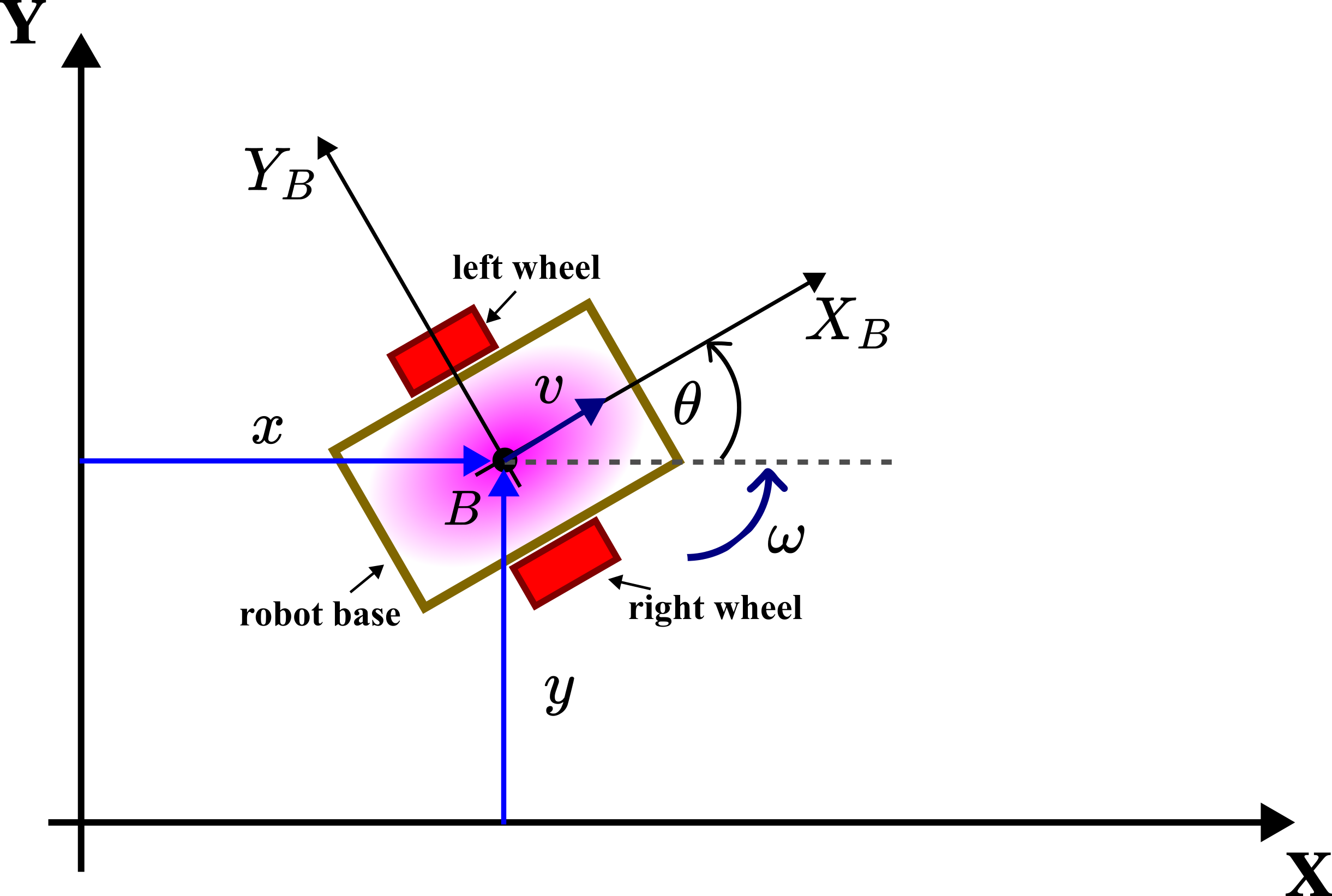
The robot consists of the robot base and two active wheels. In addition to these two wheels, there is a third passive caster wheel that provides the stability of the robotic platform (passive means that is not actively actuated, however, the wheel can still move around two perpendicular axes). This third wheel is not shown on the graph in order not to make the graph too complex. We introduce the following quantities:
- Inertial coordinate system
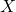 –
– (denoted by uppercase letters
(denoted by uppercase letters  and
and 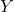 ). This coordinate system is fixed.
). This coordinate system is fixed. - Body coordinate system
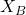 –
– 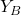 (denoted by uppercase letters
(denoted by uppercase letters 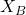 and
and 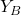 ). The body coordinate system is also called the body frame. This coordinate system is rigidly fixed to the robot body or robot base. Its center is at the point
). The body coordinate system is also called the body frame. This coordinate system is rigidly fixed to the robot body or robot base. Its center is at the point 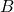 . Usually the point
. Usually the point 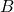 is the center of the mass or the center of the symmetry of the robot body or the robot base. The body coordinate system moves together with the robot.
is the center of the mass or the center of the symmetry of the robot body or the robot base. The body coordinate system moves together with the robot. - The coordinates
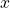 and
and 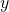 are horizontal and vertical positions of the body coordinate system
are horizontal and vertical positions of the body coordinate system 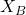 –
–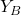 with respect to the inertial coordinate system
with respect to the inertial coordinate system 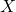 –
–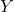 .
. - The angle
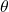 is the angle that the body coordinate system makes with the
is the angle that the body coordinate system makes with the 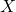 axis of the inertial coordinate system. That is, the angle
axis of the inertial coordinate system. That is, the angle 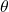 is the rotation of the body coordinate system with respect to the inertial coordinate system. The angle
is the rotation of the body coordinate system with respect to the inertial coordinate system. The angle 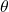 is called the orientation angle or angular orientation. This angle is also called the bearing angle (or simply bearing) or heading angle (or simply heading). Since the body coordinate system is firmly attached to the robot body the angle
is called the orientation angle or angular orientation. This angle is also called the bearing angle (or simply bearing) or heading angle (or simply heading). Since the body coordinate system is firmly attached to the robot body the angle 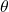 is the rotation of the robot body.
is the rotation of the robot body.  is the instantaneous velocity of the center of the body frame.
is the instantaneous velocity of the center of the body frame.  is the instantaneous angular velocity of the robot.
is the instantaneous angular velocity of the robot.
Definition of (robot) pose
Next, we need to define what is a robot pose. The (robot) pose is the vector ![]() defined by
defined by
(1) 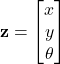
The (robot) pose completely defines the position (location) and orientation of the robot with respect to the fixed inertial frame ![]() –
–![]() . From a purely geometrical point of view, the pose defines the location and orientation of the body frame
. From a purely geometrical point of view, the pose defines the location and orientation of the body frame ![]() –
–![]() with respect to the inertial frame
with respect to the inertial frame ![]() –
–![]() . The pose is also called the kinematic state. The reason for this will be explained later on.
. The pose is also called the kinematic state. The reason for this will be explained later on.
The precise knowledge of the robot pose is important for a number of reasons. First of all, it determines the precise location and orientation of the robot in space. Secondly, the robot pose is used for feedback control. Finally, robot pose information is used in other robotic algorithms, such as path planning, obstacle avoidance, and SLAM algorithms.
Kinematic Model of Mobile Robot for Dead Reckoning
Here we present arguably the simplest possible kinematics model of the mobile robot that can be used to define and solve the dead reckoning problem. We deliberately base this tutorial on the simple kinematics model in order not to blur the main ideas of dead reckoning with too many mathematical details. Although relatively simple, this model can still be used in practical applications. We use two approaches to develop the kinematics model of the robot. The first approach is based on the discretization of the continuous-time model of the differential drive robot. This model is derived in our previous tutorial given here. The second approach is based on a simple kinematics derivation and physical intuition. Both modeling approaches result in identical models. However, the second approach is more intuitive since it is directly based on kinematics and direct physical reasoning.
Let us start with the discretization approach. In our previous tutorial, we derived the following continuous-time kinematics model of robot motion
(2) 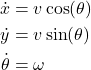
By using the forward Euler method, we discretize the model (2), as follows
(3) 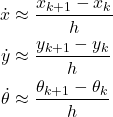
where ![]() is the discretization step,
is the discretization step, ![]() is the discrete-time instant, and
is the discrete-time instant, and ![]() and
and ![]() are the horizontal and vertical coordinates of the center of the robot body frame at the discrete-time instant
are the horizontal and vertical coordinates of the center of the robot body frame at the discrete-time instant ![]() , that is,
, that is, ![]() and
and ![]() . Similarly,
. Similarly, ![]() is the orientation of the robot body frame at the discrete-time instant
is the orientation of the robot body frame at the discrete-time instant ![]() , that is,
, that is, ![]() . Next, by using the forward Euler method and by substituting equations (3) in (2), and by replacing the approximation symbols with equality symbols, we obtain
. Next, by using the forward Euler method and by substituting equations (3) in (2), and by replacing the approximation symbols with equality symbols, we obtain
(4) 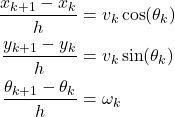
where ![]() is the instantaneous velocity at the discrete-time instant
is the instantaneous velocity at the discrete-time instant ![]() , and
, and ![]() is the instantaneous angular velocity at the discrete-time instant
is the instantaneous angular velocity at the discrete-time instant![]() . Here, it is implicitly assumed that the instantaneous velocity
. Here, it is implicitly assumed that the instantaneous velocity ![]() and angular velocity
and angular velocity ![]() are constant between the discrete-time instants
are constant between the discrete-time instants ![]() and
and ![]() .
.
From (4), we obtain the discretized kinematics model of the robot
(5) 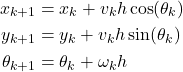
Next, we need to observe the following
- The product
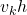 is the distance traveled in the direction of the velocity vector
is the distance traveled in the direction of the velocity vector 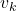 (the velocity vector is actually determined by the intensity given by
(the velocity vector is actually determined by the intensity given by 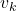 and direction determined by the angle
and direction determined by the angle 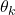 ). It should be kept in mind that the velocity vector is constant between the time instants
). It should be kept in mind that the velocity vector is constant between the time instants 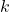 and
and 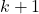 . The distance traveled between the time instants
. The distance traveled between the time instants 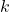 and
and 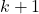 is denoted by
is denoted by(6)
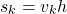
- Since
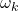 is the angular velocity, the product
is the angular velocity, the product 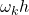 is the rotation angle of the robot body between the discrete-time instant
is the rotation angle of the robot body between the discrete-time instant 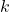 and
and 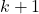 . We denote this angle by
. We denote this angle by (7)
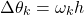
Finally, by using (6) and (7), the final discretized model of the robot kinematics takes the following form
(8) 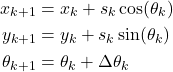
If we ignore the last equation in (8), the resulting two equations
(9) ![]()
describe the translation of the robot body along the direction of the instantaneous velocity vector, where the orientation angle ![]() remains constant. On the other hand, if we ignore the first two equations in (8), and if we only consider the last equation
remains constant. On the other hand, if we ignore the first two equations in (8), and if we only consider the last equation
(10) ![]()
then, this equation describes the rotation for the angle of ![]() . That is, the motion is decomposed (decoupled) into translation and rotation. This is a very well-known fact in kinematics and dynamics of motion of rigid bodies in a plane. Namely, the complex motion of a body in a plane from one pose to another can be decomposed into translation and rotation.
. That is, the motion is decomposed (decoupled) into translation and rotation. This is a very well-known fact in kinematics and dynamics of motion of rigid bodies in a plane. Namely, the complex motion of a body in a plane from one pose to another can be decomposed into translation and rotation.
Let us not use this principle to rederive the kinematics model (8) by using a more intuitive approach that does not explicitly rely upon the model discretization.
We formally decompose the motion of the robot from the starting point (at the discrete-time ![]() ) to the endpoint (at the discrete-time instant
) to the endpoint (at the discrete-time instant ![]() ) as follows
) as follows
- From the starting point
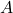 (location at the discrete-time instant
(location at the discrete-time instant 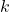 ) to the endpoint
) to the endpoint 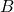 (location at the discrete-time instant
(location at the discrete-time instant 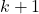 ), the robot moves along a straight line. That is, during the motion from the point
), the robot moves along a straight line. That is, during the motion from the point 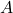 to the point
to the point 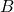 , the orientation angle
, the orientation angle 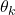 is constant, and the position coordinates
is constant, and the position coordinates 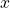 and
and 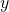 are changing.
are changing. - At the point
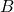 , the orientation angle
, the orientation angle 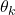 is changed, such that the orientation becomes
is changed, such that the orientation becomes 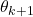 .
.
This is just a formal mathematical decomposition of the motion, since in practice, the actual motion between the two points might not look like this. This is an approximation of the motion that enables us to mathematically analyze the geometry and kinematics of motion. However, if the time interval ![]() between the time instants
between the time instants ![]() and
and ![]() is relatively small this formal decomposition relatively accurately approximates the true motion. Also, it is important to keep in mind that at the time instants
is relatively small this formal decomposition relatively accurately approximates the true motion. Also, it is important to keep in mind that at the time instants ![]() and
and ![]() the locations and orientations correspond to the real locations and orientations of the robot. What happens in between the time instants
the locations and orientations correspond to the real locations and orientations of the robot. What happens in between the time instants ![]() and
and ![]() cannot be exactly modeled unless a more complex mathematical model is used.
cannot be exactly modeled unless a more complex mathematical model is used.
To repeat, from the mathematical point of view, the motion is decomposed into a series of straight-line motions and orientation changes. Let us illustrate this with the example shown in the figure below.
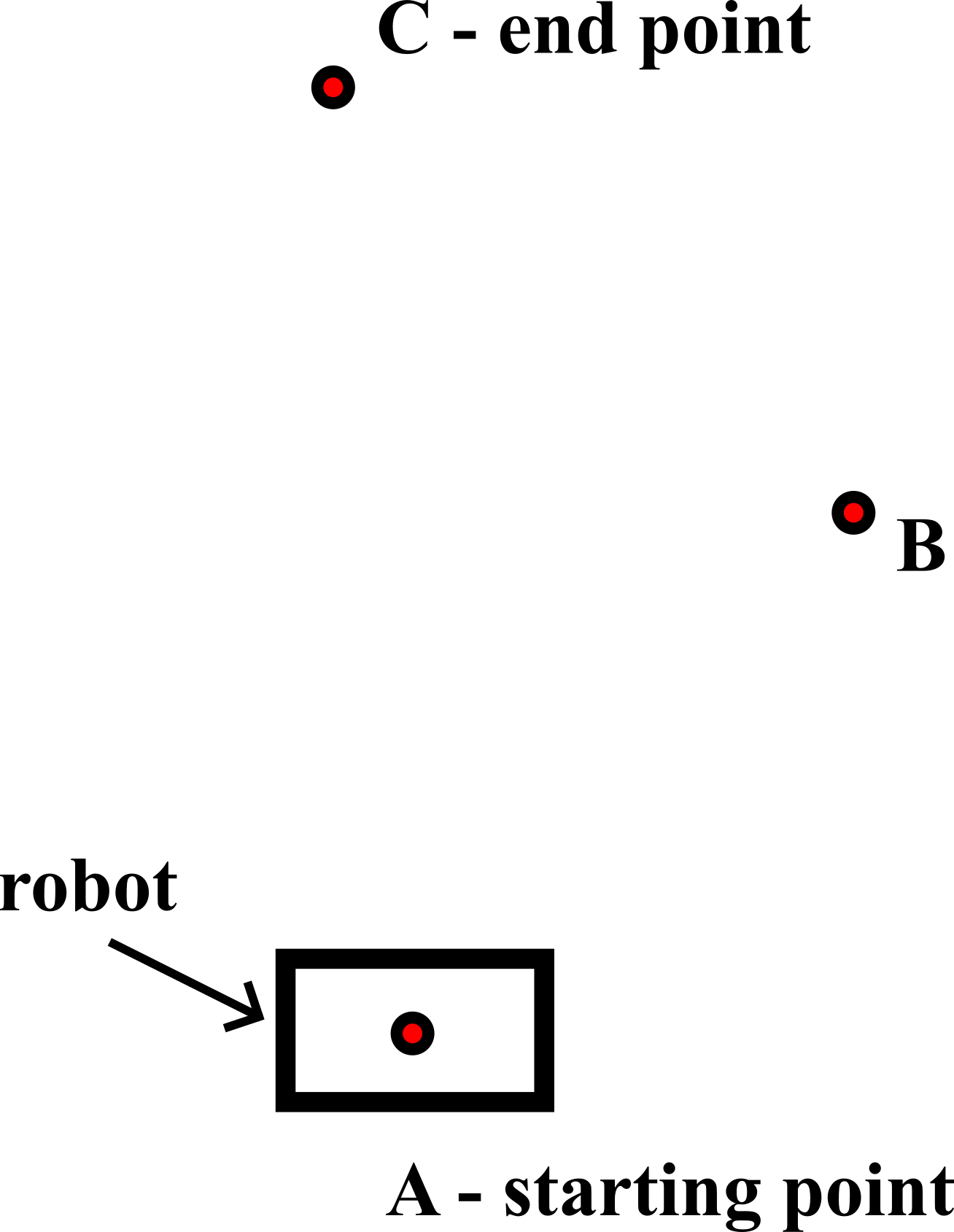
The goal is to move from the point ![]() to the point
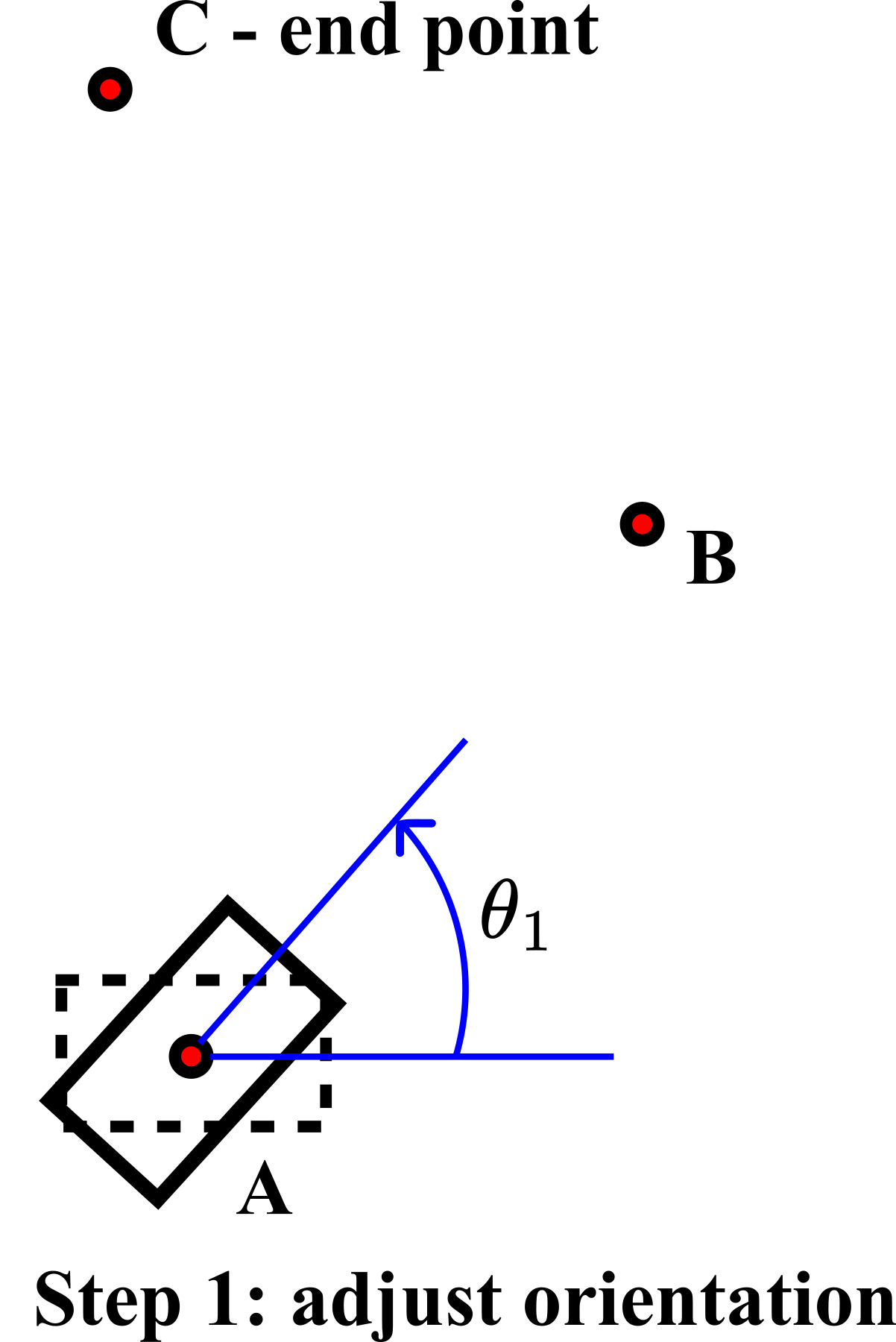
to the point ![]() . The first step, while we are still in the point
. The first step, while we are still in the point ![]() , is to adjust the orientation
, is to adjust the orientation ![]() , such that the robot can move along the straight line from the point
, such that the robot can move along the straight line from the point ![]() to the point
to the point ![]() . This is shown in the figure below.
. This is shown in the figure below.
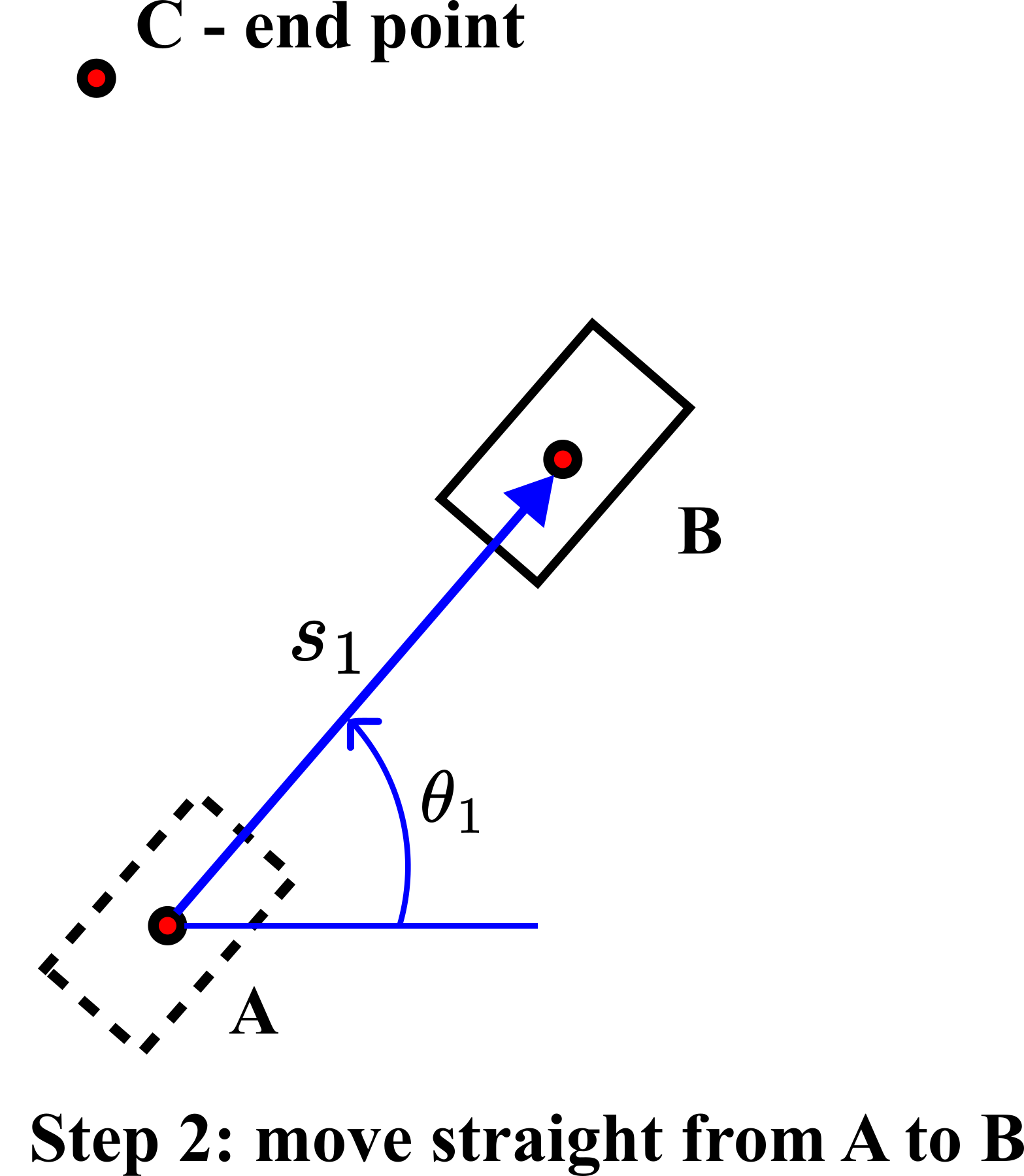
In step 2, we move from the point A to the point ![]() along the straight line for the distance
along the straight line for the distance ![]() . This is shown in the figure below.
. This is shown in the figure below.
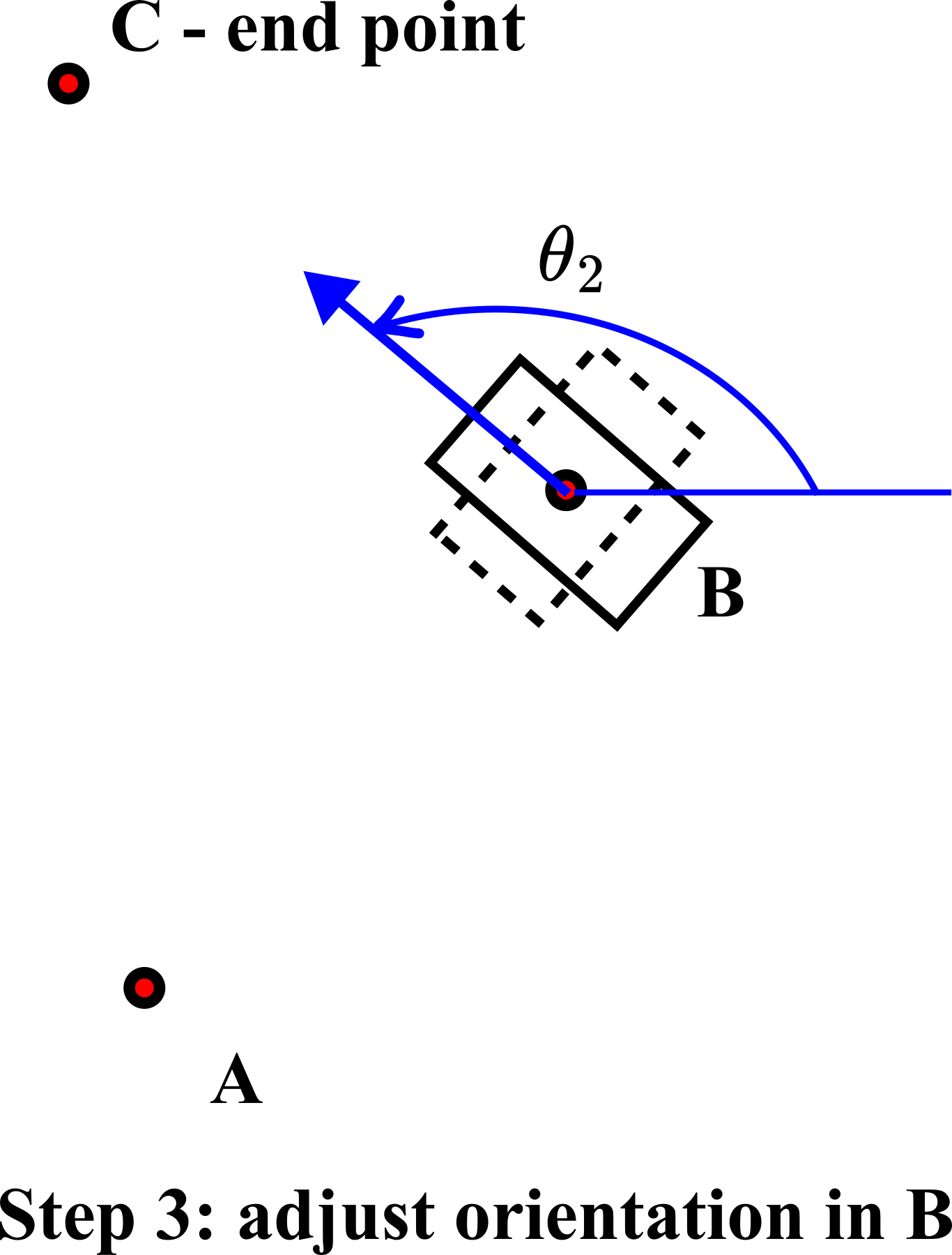
In step 3, we adjust the orientation of the robot for the angle ![]() such that we can move along the straight line from the point
such that we can move along the straight line from the point ![]() to the point
to the point ![]() .
.
 .
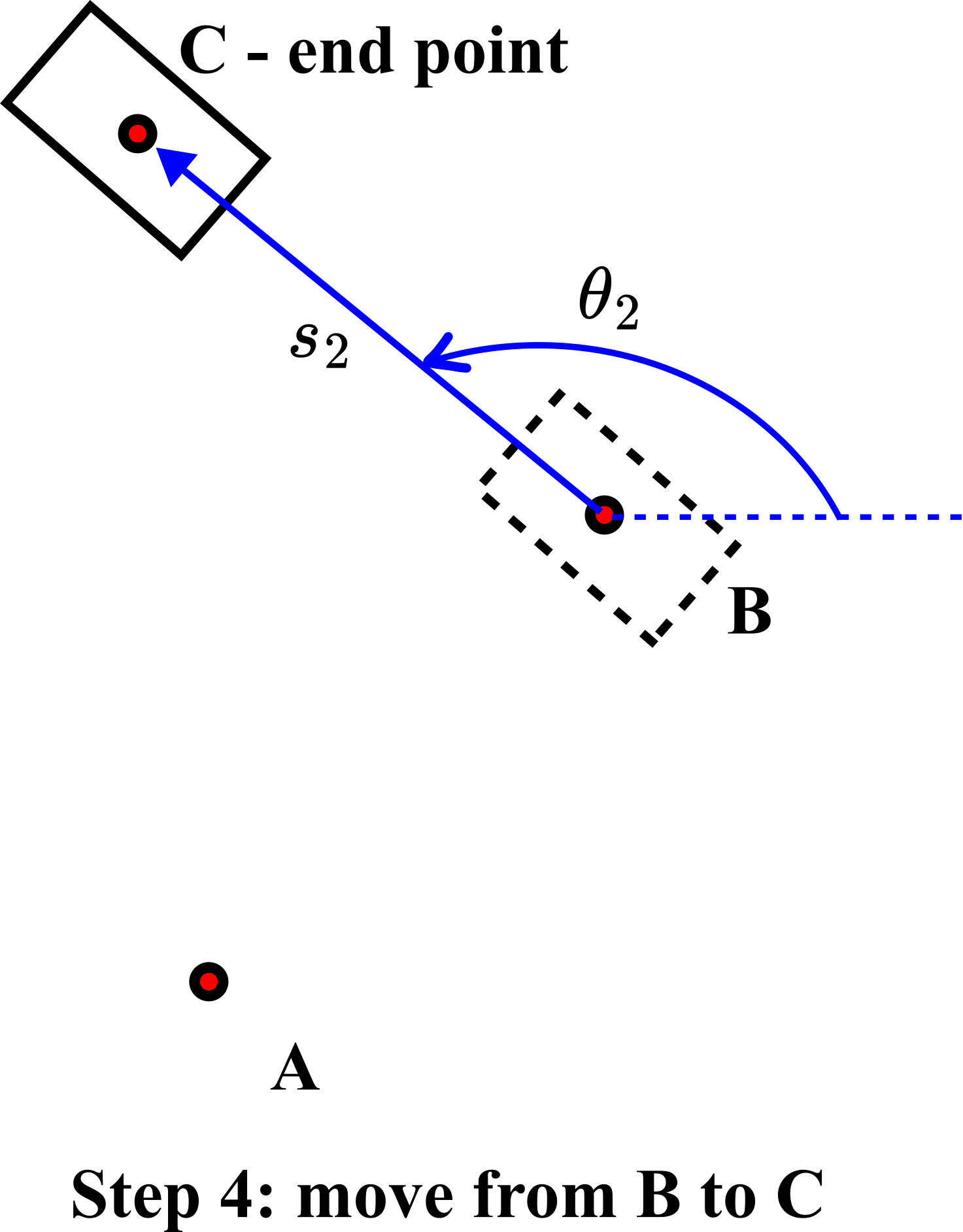
.In step 4, we move along the straight line from the point ![]() to the point
to the point ![]() for the distance
for the distance ![]() .
.
Next, we develop the kinematics model of the robot that mathematically describes this motion. Consider the figure shown below.
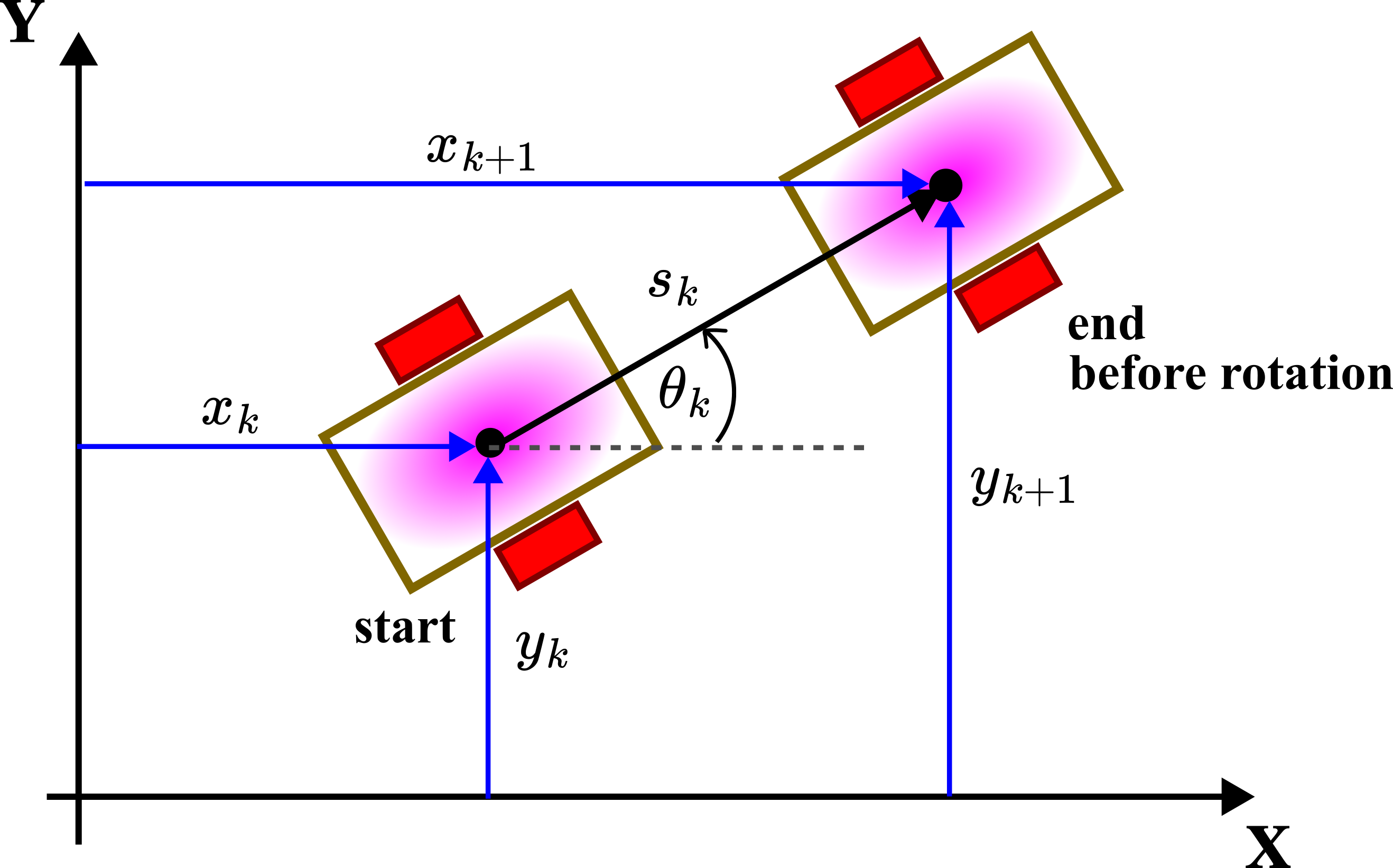
Here, we remind the reader that ![]() and
and ![]() denote the
denote the ![]() and
and ![]() coordinates of the center of the robot body at the discrete time instant
coordinates of the center of the robot body at the discrete time instant ![]() . That is,
. That is,
(11) ![]()
where ![]() is the discretization step. That is, we look at the location of the robot
is the discretization step. That is, we look at the location of the robot ![]() at the discrete-time instants
at the discrete-time instants ![]() . Similarly, we have previously defined
. Similarly, we have previously defined ![]() as follows
as follows
(12) ![]()
From the discrete-time instant ![]() to the discrete-time instant
to the discrete-time instant ![]() , the robot travels from the start to the end position shown in the figure above. During that time interval, the robot had traveled the distance of
, the robot travels from the start to the end position shown in the figure above. During that time interval, the robot had traveled the distance of ![]() . This is precisely the distance introduced in (6). Under the assumption that the orientation
. This is precisely the distance introduced in (6). Under the assumption that the orientation ![]() remains constant, from the geometry shown in Figure 7 above, we have
remains constant, from the geometry shown in Figure 7 above, we have
(13) ![]()
These equations describe the location of the robot at the time instant ![]() , under the assumption that the robot was at the location
, under the assumption that the robot was at the location ![]() at the discrete time instant
at the discrete time instant ![]() and that it had traveled the distance of
and that it had traveled the distance of ![]() between the discrete-time instants
between the discrete-time instants ![]() and
and ![]() . In addition to these equations, we need to add an equation describing the change of the orientation angle
. In addition to these equations, we need to add an equation describing the change of the orientation angle ![]() . For that purpose, consider the figure below.
. For that purpose, consider the figure below.
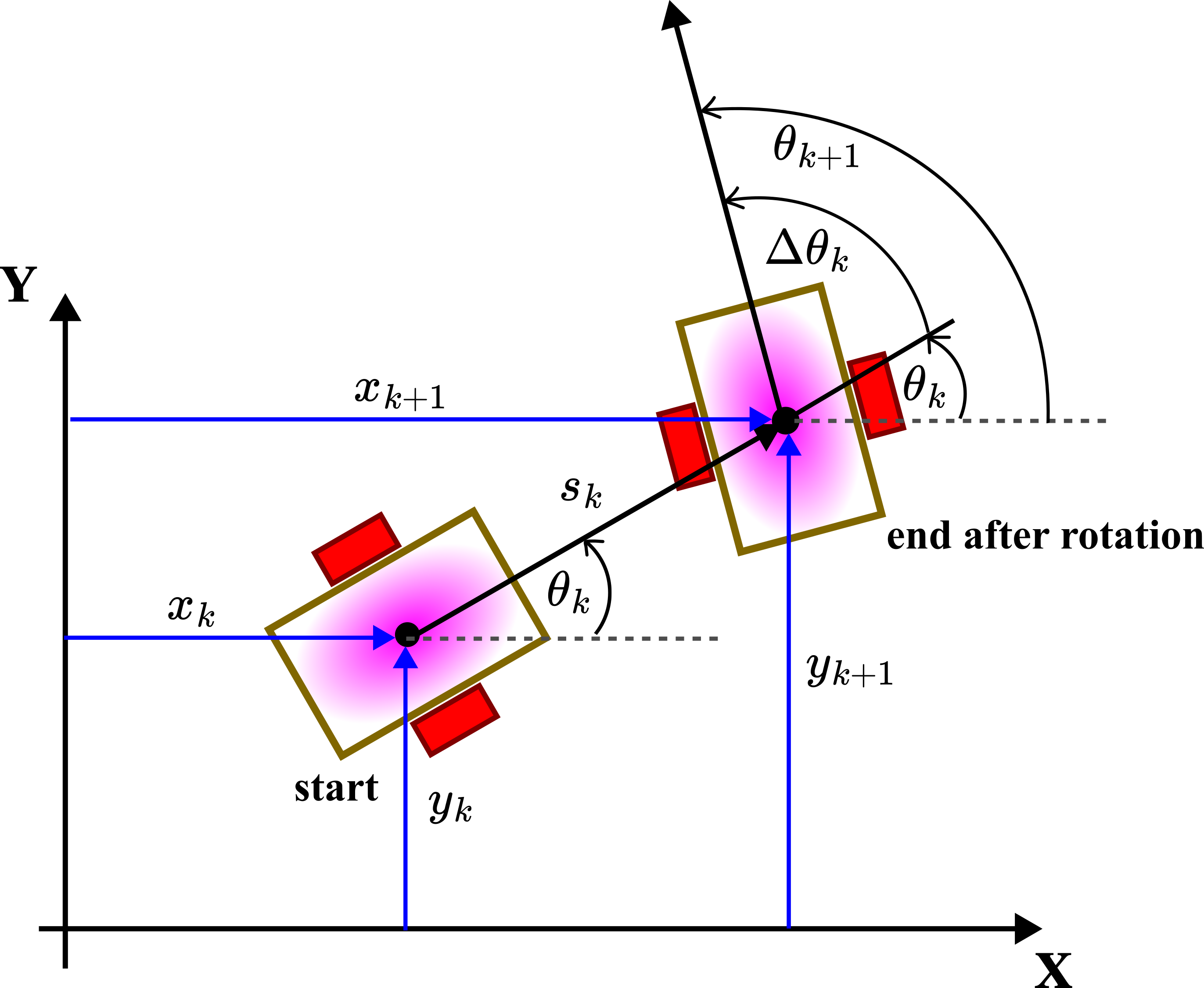
In the endpoint, we perform the rotation for the angle ![]() that is first introduced in equation (7). That is, the final orientation at the discrete-time instant
that is first introduced in equation (7). That is, the final orientation at the discrete-time instant ![]() is
is
(14) ![]()
By combining (13) and (14), we obtain the final kinematics model of the mobile robot
(15) 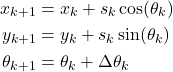
That is precisely the kinematics model (8) obtained by using discretization.
Dead Reckoning Using Kinematics Model and Python Simulations
Here, we first define the dead reckoning problem, and then, we explain how to use the derived kinematics model (15) (or (8)) to solve the dead reckoning problem. In the second part of this tutorial series (link will be posted later on), we explain how to implement the dead reckoning method in Python and through simulations, we explain several issues with dead reckoning.
First, let us define the pose vector. The pose vector, denoted by ![]() , is defined by
, is defined by
(16) 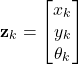
Next, let us define an estimate of the pose vector. The estimate of the pose vector, denoted by ![]() , is defined by
, is defined by
(17) 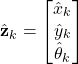
where ![]() ,
, ![]() , and
, and ![]() are estimates of
are estimates of ![]() ,
, ![]() , and
, and ![]() that are computed by using the dead reckoning method.
that are computed by using the dead reckoning method.
The dead reckoning problem can be formally described as follows.
Dead reckoning problem. Let us assume that
- The estimate of the robot pose vector
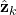 at the discrete-time instant
at the discrete-time instant 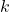 is known.
is known. - The measurements of the traveled distance
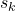 and orientation change
and orientation change 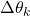 are obtained at the discrete-time instant
are obtained at the discrete-time instant 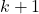 .
. - The initial values
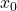 ,
, 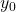 , and
, and 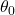 are known accurately. That is, the initial pose vector
are known accurately. That is, the initial pose vector 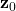 is known accurately.
is known accurately.
Then, under these assumptions, obtain an estimate of the robot pose vector ![]() at the time instant
at the time instant ![]() . Perform the estimation tasks recursively for
. Perform the estimation tasks recursively for ![]() .
.
To solve this problem and to implement its solution in Python, we need to clarify several important aspects of this problem.
First of all, we need to explain what is odometry. Often, in robotics literature or during the conversation between robotics engineers you will hear the term “odometry”. People use this term in different contexts and have different understandings of this term. Under the term “odometry” we understand the process of using the data from sensors to estimate/measure the traveled distance and heading direction (orientation of the robot). Some people restrict the term odometry only to the sensing (measurement) process, and some people under the term odometry understand the complete process of sensing and estimating the distance and heading direction. In this tutorial, under the term odometry we understand both the sensing and estimation process. In that sense, dead reckoning is a type of odometry.
Now, the main question is how to measure the distance traveled ![]() and the change of angle
and the change of angle ![]() ? We can measure
? We can measure ![]() indirectly by using wheel encoders. By knowing the encoder resolution, wheel geometry, and number of detected encoder pulses, we can obtain the measurement of
indirectly by using wheel encoders. By knowing the encoder resolution, wheel geometry, and number of detected encoder pulses, we can obtain the measurement of ![]() . Also, we can measure
. Also, we can measure ![]() by using some other method (more about this in our future tutorials). On the other hand, we can measure
by using some other method (more about this in our future tutorials). On the other hand, we can measure ![]() by using a gyroscope, compass, or even using two wheel encoders and combining their measurements (more about this in our future tutorials).
by using a gyroscope, compass, or even using two wheel encoders and combining their measurements (more about this in our future tutorials).
One of the most important issues that limit the accuracy of odometry and dead reckoning is that measurements of ![]() and
and ![]() contain errors. For example, the wheels of the robot can slip. However, the encoder will detect the wheel rotation angle, and the traveled distance computed on the basis of the detected wheel angle will NOT correspond to the actual traveled distance. Also, some random effects can occur that can limit the accuracy of sensors.
contain errors. For example, the wheels of the robot can slip. However, the encoder will detect the wheel rotation angle, and the traveled distance computed on the basis of the detected wheel angle will NOT correspond to the actual traveled distance. Also, some random effects can occur that can limit the accuracy of sensors.
This means that in the model (8), we are not directly measuring ![]() and
and ![]() . Instead, we are measuring their corrupted versions
. Instead, we are measuring their corrupted versions ![]() and
and ![]() defined as follows
defined as follows
(18) ![]()
where ![]() and
and ![]() are measurement errors. We assume that both
are measurement errors. We assume that both ![]() and
and ![]() are normally distributed with zero mean and known variances. That is, we assume
are normally distributed with zero mean and known variances. That is, we assume
(19) ![]()
where ![]() and
and ![]() are the variances of
are the variances of ![]() and
and ![]() , respectively.
, respectively.
Here, it is very important to keep in mind that the true values of ![]() and
and ![]() are not known! The only quantities that we know and that we can use for solving the dead reckoning problem are their measurements
are not known! The only quantities that we know and that we can use for solving the dead reckoning problem are their measurements ![]() and
and ![]() . These measurements are corrupted by the measurement noise, represented by
. These measurements are corrupted by the measurement noise, represented by ![]() and
and ![]() .
.
In the sequel, we present the simplest possible approach for solving the dead reckoning problem. This approach is suboptimal and in some sense “naive”. However, this approach is still very useful since it can give us the first idea of the behavior of the dead reckoning. The idea for solving this problem is to use the kinematic model (8) and to substitute the true values of the distance ![]() and angle change
and angle change ![]() by their measurements
by their measurements ![]() and
and ![]() . Also, the exact values are substituted by estimates in order to obtain a recursive relation for computing the estimates. The (naive) dead reckoning estimator has the following form:
. Also, the exact values are substituted by estimates in order to obtain a recursive relation for computing the estimates. The (naive) dead reckoning estimator has the following form:
(20) 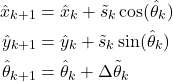
We initialize the equations (20) with the exact initial value of the location and orientation, that is
(21) 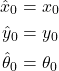
After that, by using the measurements ![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() , we propagate the equation (20), to compute the estimates
, we propagate the equation (20), to compute the estimates ![]() .
.