In this Python tutorial, we explain how to solve a system of nonlinear equations in Python by using the fsolve() function and by specifying the Jacobian matrix. In our previous tutorial, whose link can be found here, we explained how to solve systems of nonlinear equations without specifying the Jacobian matrix. The main advantage of specifying the Jacobian matrix is that we can significantly speed the convergence of the nonlinear solver implemented in fsolve() (actually fsolve is just a wrapper, but this is not important at this point). This is very important for large-scale nonlinear systems, where we need to approximate solution in a reasonable time interval. However, in order to specify the Jacobian matrix, we need to be able to analytically compute the partial derivatives. For small problems, we can do that by hand. However, for large-scale problems, this task might become complex. For large-scale problems, we need to use automatic differentiation techniques. More about this in our next tutorials.
The function fsolve() can only solve square systems of nonlinear equations. That is, the number of unknown variables has to be equal to the number of equations in the system. According to the documentation, this function is actually a wrapper for the hybrid Powell method implemented in the FORTRAN90 library MINPACK. In our next tutorials, we will explain how to solve in Python overdetermined and underdetermined systems of nonlinear equations.
The YouTube tutorial accompanying this post is given here:
Test Case and Preliminary Transformations and Computations
We consider the following system of nonlinear equations
(1) 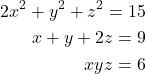
where ![]() , and
, and ![]() are the unknown variables that we want to determine. This system has at least one solution that is
are the unknown variables that we want to determine. This system has at least one solution that is ![]() , and
, and ![]() . We can verify that this is the solution by substituting these values in the original system:
. We can verify that this is the solution by substituting these values in the original system:
(2) 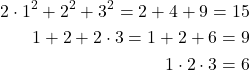
This solution will be used as a test case to test the accuracy of the function fsolve(). It is important to note that while performing simulations, we found another solution:
(3) ![]()
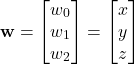
To solve this system in Python, we first need to group the variables in a vector. Let us define the vector ![]() (the symbol for the vector can be arbitrary) that gathers the original variables
(the symbol for the vector can be arbitrary) that gathers the original variables ![]() as follows:
as follows:
(4) 
that is
(5) ![]()
where in order to be consistent with Python indexing, we start the index of the variables ![]() from 0.
from 0.
The next step is to use the new notation (4) to write the original system in a vector form given by the following equation
(6) ![]()
where ![]() is a 3 by 1 vector function. By using (4), from (1), we have
is a 3 by 1 vector function. By using (4), from (1), we have
(7) 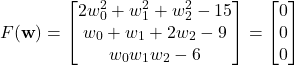
The Jacobian matrix of the system (7) is defined as follows
(8) 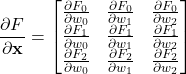
where ![]() and
and ![]() are the entries of the vector function
are the entries of the vector function ![]() :
:
(9) 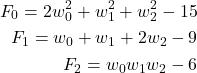
By computing the partial derivatives, we obtain the final form of the Jacobian matrix:
(10) 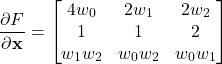
Python Implementation with Analytical Jacobian Matrix
The first step is to import the necessary libraries.
import numpy as np
from scipy.optimize import fsolve
Then, we need to define the function ![]() given by (7). That is, we need to define a function that accepts a vector argument
given by (7). That is, we need to define a function that accepts a vector argument ![]() and that returns the value of the function
and that returns the value of the function ![]() . The function is given below.
. The function is given below.
# for a given variable w, this function returns F(w)
# if w is the solution of the nonlinear system, then
# F(w)=0
# F can be interpreted as the residual
def nonlinearEquation(w):
F=np.zeros(3)
F[0]=2*w[0]**2+w[1]**2+w[2]**2-15
F[1]=w[0]+w[1]+2*w[2]-9
F[2]=w[0]*w[1]*w[2]-6
return F
The next step is to define a Python function that will accept a vector argument ![]() , and that will compute the Jacobian matrix for this vector argument. The function is given below.
, and that will compute the Jacobian matrix for this vector argument. The function is given below.
# this function returns 3 by 3 matrix defining
# the Jacobian matrix of F at the input vector w
def JacobianMatrix(w):
JacobianM=np.zeros((3,3))
JacobianM[0,0]=4*w[0]
JacobianM[0,1]=2*w[1]
JacobianM[0,2]=2*w[2]
JacobianM[1,0]=1
JacobianM[1,1]=1
JacobianM[1,2]=2
JacobianM[2,0]=w[1]*w[2]
JacobianM[2,1]=w[0]*w[2]
JacobianM[2,2]=w[0]*w[1]
return JacobianM
Both the function “nonlinearEquation” and “JacobianMatrix” will be provided as input arguments to the function fsolve(). Since fsolve() uses an iterative method to find the solution, we need to provide an initial guess of the solution that is updated iteratively by the fsolve() function. We generate this initial guess as a random vector, and we call the fsolve() function. This is done by the following code lines:
# generate an initial guess
initialGuess=np.random.rand(3)
# solution
solutionTuple=fsolve(nonlinearEquation,initialGuess,fprime=JacobianMatrix,full_output=1)
In our case, the fsolve() function accepts three arguments:
- The name of the function that defines the system of nonlinear equations. In our case, the name is “nonlinearEquation”.
- Initial guess of the solution. In our case, it is “initialGuess”.
- The function defining the Jacobian matrix is specified by the third argument: “fprime=JacobianMatrix”
- Additional parameters. In our case, we are using only a single additional parameter “full_output=1”. This means that we will force the fsolve() function to return not only the final converged solution, but also a complete data structure containing all the information about the computed solution and the solution process.
Of course, fsolve() can accept additional parameters, such as tolerances, number of iterations, etc. The webpage whose link is given here explains these parameters.
The output of the function is
(array([1., 2., 3.]),
{‘nfev’: 20,
‘njev’: 3,
‘fjac’: array([[-0.44997594, -0.14844783, -0.8806162 ],
[ 0.8377442 , 0.27143046, -0.47382503],
[-0.30936436, 0.95094098, -0.00222413]]),
‘r’: array([-6.73637341, -4.1530185 , -3.8486437 , 1.41286067, 3.05068533,
0.63161467]),
‘qtf’: array([-7.28229968e-09, -1.09839137e-09, -8.23294722e-10]),
‘fvec’: array([4.43378667e-12, 0.00000000e+00, 1.16537890e-11])},
1,
‘The solution converged.’)
The first entry of this tuple is the computed solution: it is [1., 2., 3.]. Note that this is the first solution. If we run the code again with a different random initial guess, we will most likely obtain the second solution: [1.16022233, 1.67875447, 3.0805116 ]. The second entry “nfev” is the number of function evaluations. Another important parameter is the parameter “fvec”. This is the function ![]() evaluated at the computed solution. This value can be seen as the residual and it can quantify how accurately our computed solution solves the equation. An explanation of other parameters can be found here.
evaluated at the computed solution. This value can be seen as the residual and it can quantify how accurately our computed solution solves the equation. An explanation of other parameters can be found here.
We can extract the solution and manually compute the residual, as follows
#extract the solution
solution=solutionTuple[0]
# compute the residual
residual=nonlinearEquation(solution)