Solve Differential Equations Analytically Using MATLAB Symbolic Math Toolbox – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this lecture, we explain how to solve differential equations analytically using MATLAB Symbolic Math Toolbox. Furthermore, we explain how to plot a graph of the derived analytical solution. The YouTube video accompanying this post is given below.

Consider the following linear ordinary differential equation

(1) $\begin{align*}m\ddot{d}+k_{d}\dot{d}+k_{s}d=F(t)\end{align*}$

where $d=d(t)$ is the variable we want to solve for, $\dot{d}=\frac{dd}{dt}$ , $\ddot{d}=\frac{d\dot{d}}{dt}$ , $m,k_{d}$ , and $k_{s}$ are constants, and $F(t)$ is the specified function of time. For example, as we have explained in our previous lecture, the equation (1) can represent a mass-spring-damper system that is driven by the force $F(t)$ .

Our goal is to derive an analytical solution of (1) using MATLAB Symbolic Toolbox.

The first step is to define the symbolic variables. This can be done as follows.

syms d(t) kd ks mass Force(t)

Here we specify that $d(t)$ , $kd$ , $ks$ , and $Force(t)$ are symbolic variables, that correspond respectively to the variables and constants $d$ , $k_{d}$ , $k_{s}$ , and $F$ in (2). Here it should be emphasized that it is important to define $d$ and $F$ as functions of time. This is achieved by typing $d(t)$ and $Force(t)$ .

The next step is to define the first and second derivatives of $d$ . This can be done as follows.

ddot_d=diff(d,t,2)
dot_d=diff(d,t,1)

Let us assume that the variable $F$ is equal to $sin(t)$ . For such a choice of the right-hand side of Eq. (2), we define the differential equation as follows

dynamics_equation=mass*ddot_d+kd*dot_d+ks*d == sin(t)

This code is self-explanatory. To be able to solve the differential equation, we need to specify the initial conditions for $d(0)$ and $\dot{d}(0)$ (position and velocity). This can be done as follows.

initial_conditions=[d(0)==1, dot_d(0)==0]

We solve the equation by executing the following line of code.

solution=dsolve(dynamics_equation,initial_conditions)

We can also simplify the solution by executing the following line of code.

solution2=simplify(solution)

The next step is to plot the solution. In order to plot the solution, we need to select the values of the parameters $m$ , $k_{d}$ , and $k_{s}$ . This can be done by executing the following line of code.

solution3=subs(solution2,{mass,ks,kd},{2,1,0.1})

That is, we choose $m=2$ , $k_{s}=1$ , and $k_{d}=0.1$ . We can also simplify or expand the substituted solution as follows.

solution4=simplify(solution3)

solution5=expand(solution3)

Finally, the substituted solution can be plotted by executing the following code lines.

plotting_interval=[0,100]

fplot(solution4,plotting_interval)
xlabel('time')
ylabel('solution')

First, we choose the plotting interval, and then similarly to the MATLAB function plot(), we can use the function $fplot()$ to plot the solution. The result is shown in the figure below.

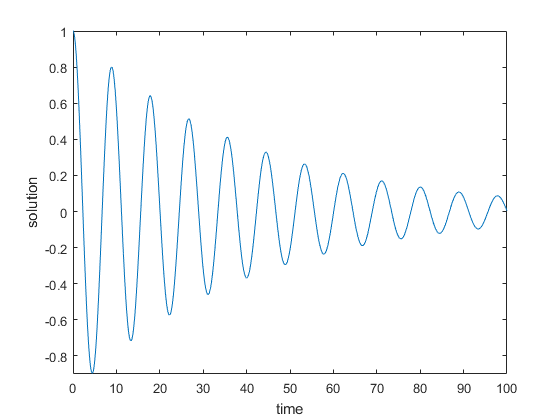
Finally, let us verify that this approach produces accurate results. The idea is to compare this approach with another approach for computing the analytical solution. The two approaches should produce results that match. The approach that is used for comparison is based on the Laplace transform. We perform the tests using the following differential equation

(2) $\begin{align*}\ddot{d}+4d=t\end{align*}$

where $t$ is time variable. Let us assume that initial conditions are $d(0)=1$ and $\dot{d}(0)=0$ . Let us apply the Laplace transform to equation (2). Let $D(s)$ be the Laplace transform of $d(t)$ . By applying the Laplace transform to (2), we obtain

(3) $\begin{align*}s^2 D(s) -s d(0) -\dot{d}(0)+4D(s)=\frac{1}{s^2}\end{align*}$

Taking into account that $d(0)=1$ and $\dot{d}(0)=0$ , and by transforming the expression (3), we obtain

(4) $\begin{align*}D(s)=\frac{s}{s^{2}+4}+\frac{1}{s^2}\cdot \frac{1}{s^2+4}\end{align*}$

By applying the inverse Laplace transform to (4), we can obtain $d$ as function of $t$ . We use MATLAB to compute the inverse Laplace transform. The inverse Laplace transform can be computed by executing the following code lines

syms s 

Ds=s/(s^2+4)+(1/(s^2))*(1/(s^2+4))

inverseLaplace=ilaplace(Ds)
simplify(inverseLaplace)

The result is

t/4 + cos(2t) – sin(2t)/8

Let us now compute the solution by analytically solving the equation (2). The code for solving this equation is given below.

clear, pack, clc
syms d(t) 

ddot_d=diff(d,t,2)
dot_d=diff(d,t,1)

dynamics_equation=ddot_d+4*d == t

initial_conditions=[d(0)==1, dot_d(0)==0]

solution=dsolve(dynamics_equation,initial_conditions)

solution2=simplify(solution)

The results is

t/4 + cos(2t) – sin(2t)/8

We can see that the two approaches produce the identical results.

admin

You might also like

Application of Routh Stability Criterion to Select Parameters of Proportional Integral (PI) Controllers

Forward Robot Kinematics Using Homogeneous Transform

Introduction to MATLAB Control System Toolbox – Defining Models and Computing Responses