PID Controller Discretization and Implementation in Arduino – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this post, we explain how to discretize and implement a Proportional Integral Derivative (PID), controller. To demonstrate the PID controller implementation, we use a ball beam system and an Arduino microcontroller.

In the s-domain the PID controller has the following form

(1) $\begin{align*}U(s)=K\big(1+\frac{1}{sT_{i}}+sT_{d}\big)E(s)\end{align*}$

where $U(s)$ is the control action that is sent to the actuator, E(s) is the control error defined by

(2) $\begin{align*}E(s)=Y_{r}(s)-Y(s)\end{align*}$

where $Y_{r}(s)$ is the desired value of the output (also refered to as the set point or reference value) and $Y(s)$ is the system output. In 1, $K$ is the proportional gain, $T_{i}$ is the integral time, and $T_{d}$ is the derivative time. These are control parameters that need to be tuned. The controller 1 is in the standard or non-interacting form.

In the time domain, the PID controller 1, has the following form

(3) $\begin{align*}u(t)=K\big(e(t)+\frac{1}{T_{i}}\int_{0}^{t} e(\tau) d\tau +T_{d} \dot{e}(t)\big)\end{align*}$

where

(4) $\begin{align*}e(t)=y_{r}(t)-y(t)\label{error}\end{align*}$

To obtain 3 from 1, we used the following Laplace transform pairs (by neglecting constants):

(5) $\begin{align*}\dot{e}(t) \rightarrow s E(s) \\ \int_{0}^{t} e(\tau) d\tau \rightarrow \frac{1}{s} E(s)\end{align*}$

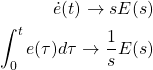
The controller 3 is the continious-time domain. However, to implement the controller using microcrontrollers we need to discretize the controller. There are several ways for discretizing the controller. In this post, we will use the simplest method (by the author’s opinion). To implement the controller, we first differentiate the equation 3:

(6) $\begin{align*}\dot{u}(t)=K\dot{e}(t)+\frac{K}{T_{i}}e(t) +KT_{d} \ddot{e}(t)\end{align*}$

Next, using the finite difference method we approximate the first and second derivatives in 6. Due to favorable stability properties, we use backward differences. The first derivative of the control input is approximated as follows

(7) $\begin{align*}\dot{u}(t)\approx\frac{u_{k}-u_{k-1}}{h}\end{align*}$

where $h$ is a discretization constant, $u_{k}=u(kh)$ , $k=0,1,2,\ldots$ and $k$ is a discrete-time instant. At the discrete-time $kh$ , the control action $u_{k}$ is sent to an actuator. By introducing this approximation, we have introduced an additional parameter that needs to be selected. This parameter is the discretization constant $h$ . Later in this post, we give some guideiness for selecting this constant.
Similarly, we approximate the first derivative of the control error

(8) $\begin{align*}\dot{e}(t)\approx \frac{e_{k}-e_{k-1}}{h}\end{align*}$

The second derivative of the control error is approximated as follows

(9) $\begin{align*}\ddot{e}(t)\approx\frac{\dot{e}_{k}-\dot{e}_{k-1}}{h}\end{align*}$

By substituting \eqref{firstDerivativeApproximationError} for the time indices $k$ and $k-1$ , we obntain

(10) $\begin{align*} \ddot{e}(t)\approx\frac{e_{k}-2e_{k-1}+e_{k-2}}{h^2} \end{align*}$

By substituting the approximations 7, 8, and 10 in 6, we obtain the final expression for the control signal at the time instant $k$

(11) $\begin{align*}u_{k}=u_{k-1}+K_{0}e_{k}+K_{1} e_{k-1}+K_{2}e_{k-2} \end{align*}$

where the constants $K_{0}$ , $K_{1}$ , and $K_{2}$ are determined as follows

(12) $\begin{align*}K_{0}& =K\Big(1 + \frac{h}{T_{i}}+\frac{T_{d}}{h} \Big) \\K_{1}&=-K(1+\frac{2T_{d}}{h}) \\K_{2}&=\frac{KT_{d}}{h}\end{align*}$

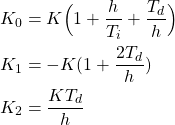
From 11 we see that the control action at the time instant $k$ is equal to the control action at the time instant $k-1$ plus the weighted sum of the errors at the time instants $k$ , $k-1$ , and $k-2$ . This form of the PID controller can easily be implemented in a microcontroller. The control loop consists of the following steps:

for k=0,1,2,3,…
1. Obtain sensor measurements.
2. Compute the control signal $u_{k}$ given by 11
3. Send the control signal $u_{k}$ .
4. Wait for $h_{1}$ seconds.

where $h_{1}$ is an additional delay introduced in the loop. The time of executing the steps 1-3 plus the time $h_{1}$ should be equal to the discretization step $h$ . There are several methods for choosing the discretization constant. We explain a simple method that does not require additional mathematical explanation.
The discretization step is chosen on the basis of how fast the system response is. Namely, we can apply a step control input $u=const$ and on the basis of the response, we can identify a rise time . Then we can select the discretization constant to be 10-20 smaller than the rise time. However, we should always keep in mind that the discretization constant is large enough such that the steps 1-3 in the control loop can be computed. These steps also contain additional substeps that will be explained in the sequel. In practice, we can measure the time it takes for the steps 1-3 to execute, and then we can select an additional delay time $h_{1}$ , such that the total time is equal to the discretization constant.

In the sequel, we present the code that implements the PID controller. The code can be found here. We use the ball-beam system that is used in the following video to demonstrate the PID controller tuning.

//sensor parameters

int distanceSensorPin = A0;   // distance sensor pin
float Vr=5.0;                 // reference voltage for A/D conversion
float sensorValue = 0;        // raw sensor reading
float sensorVoltage = 0;      // sensor value converted to volts 
float k1=16.7647563;          // sensor parameter fitted using the least-squares method
float k2=-0.85803107;         // sensor parameter fitted using the least-squares method
float distance=0;             // distance in cm       
int noMeasurements=200;        // number of measurements for averaging the distance sensor measurements 
float sumSensor;              // sum for computing the average raw sensor value

// motor parameters
#include <Servo.h>
Servo servo_motor; 
int servoMotorPin = 9;        // the servo motor is attached to the 9th Pulse Width Modulation (PWM)Arduino output


// control parameters
float desiredPosition=35;     // desired position of the ball
float errorK;                 // position error at the time instant k
float errorKm1=0;             // position error at the time instant k-1
float errorKm2=0;             // position error at the time instant k-2
float controlK=0;             // control signal at the time instant k
float controlKm1=0;           // control signal at the time instant k-1
int delayValue=0;             // additional delay in [ms]

float Kp=0.2;                        // proportional control 
float Ki=10;                         // integral control
float Kd=0.4;                        // derivative control
float h=(delayValue+32)*0.001;       // discretization constant, that is equal to the total control loop delay, the number 32 is obtained by measuring the time it takes to execute a single loop iteration                         

float keK=Kp*(1+h/Ki+Kd/h);               // parameter that multiplies the error at the time instant k
float keKm1=-Kp*(1+2*Kd/h);               // parameter that multiplies the error at the time instant k-1                    
float keKm2=Kp*Kd/h;                      // parameter that multiplies the error at the time instant k-2

void setup() 
{
  Serial.begin(9600);
  servo_motor.attach(servoMotorPin);
}

void loop() 
{
  unsigned long startTime = micros(); // this is used to measure the time it takes for the code to execute
  // obtain the sensor measurements
  sumSensor=0;

  // this loop is used to average the measurement noise
  for (int i=0; i<noMeasurements; i++)
  {
    sumSensor=sumSensor+float(analogRead(distanceSensorPin));  
  }
  sensorValue=sumSensor/noMeasurements;
  sensorVoltage=sensorValue*Vr/1024;
  distance = pow(sensorVoltage*(1/k1), 1/k2); // final value of the distance measurement

  
  errorK=desiredPosition-distance; // error at the time instant k;

  // compute the control signal
  controlK=controlKm1+keK*errorK+keKm1*errorKm1+keKm2*errorKm2;

  // update the values for the next iteration
  controlKm1=controlK;
  errorKm2=errorKm1;
  errorKm1=errorK;

  servo_motor.write(94+controlK); // the number 94 is the control action necessary to keep the ball in the horizontal position
 // Serial.println((String)"Control:"+controlK+(String)"---Error:"+errorK);

 // these three lines are used to plot the data using the Arduino serial plotter 
  Serial.print(errorK);
  Serial.print(" ");
  Serial.println(controlK);
  unsigned long endTime = micros();
  unsigned long deltaTime=endTime-startTime;
 // Serial.println(deltaTime);
  
 // delay(delayValue); // uncomment this to introduce an additional delay
 
}

A few comments are in order. The code lines 3-11 are used to define the sensor parameters. We are using a SHARP infrared distance sensor to measure the ball position on the beam. The procedure for calibrating the distance sensor is given in another post, and explained in the video below.

The code lines 14-16 are used to define the servo-motor parameters. The code lines 20-35 are used to define the controller parameters. The code lines 20-25 define respectively variables for $e_{k}, e_{k-1},e_{k-2},u_{k},u_{k-1}$ . The code 26 defines the variable $h_{1}$ . The code lines 28-31 define respectively $K,T_{i},K_{d},h$ . The code lines 33-35 define respectively $K_{0},K_{1}, K_{2}$ .
The code lines 44 and 77 are used to measure the time it takes for the code to execute. This is necessary for obtaining the exact value of the constant $h$ . On the basis of the measurements, we have assigned the value of the constant $h$ in the code line 31 (this required some online code testing). The code lines 47-56 are used to average the raw sensor data and to compute the distance in [cm]. For more details see this post. The code lines 59-67 are used to compute the control errors, control actions, and to update the values of errors and control actions for the next iteration. The code line 69 is used to send the control actions to the actuator. Notice that 94 corresponds to the horizontal beam position. The code lines 73-75 are used to plot the results using the Arduino serial plotter.

admin

You might also like

Tutorial on how to Execute Python Code Directly From MATLAB

Some questions for the midterm exam

Homework Assignment 4