In this calculus and linear algebra tutorial, we will learn the following topics
- What is a minor of a matrix and how to calculate minors of a matrix
- What is a cofactor of a matrix and how to calculate cofactors of a matrix
- What is an adjugate matrix and how to calculate it
- How to invert a matrix by computing minors, cofactors, and matrix adjugate
In the follow-up tutorials, we explain how to use these definitions to compute the matrix inverse. In this tutorial, we will just state the general formula of matrix inverse in terms of minors, cofactors, and matrix adjugate.
Minor of a Matrix
DEFINITION OF A MINOR OF A MATRIX: For a square matrix, the ![]() minor is equal to the determinant of a submatrix obtained by deleting the
minor is equal to the determinant of a submatrix obtained by deleting the ![]() th row and
th row and ![]() th column of the matrix.
th column of the matrix.
Alternative (not rigorous) definition of a minor: Consider the matrix ![]() with its
with its ![]() entry denoted by
entry denoted by ![]() . Then the minor
. Then the minor ![]() corresponding to the entry
corresponding to the entry ![]() is calculated as a determinant of a submatrix obtained by erasing the row and the column to which the entry
is calculated as a determinant of a submatrix obtained by erasing the row and the column to which the entry ![]() belong to.
belong to.
Now, let us learn how to calculate a minor of a matrix. The calculation of the minor is illustrated in the figure below.

In the figure above, we illustrate how to compute the minor ![]() of the 3 by 3 matrix
of the 3 by 3 matrix ![]() :
:
(1) 
Since we want to compute the minor ![]() , corresponding to the entry
, corresponding to the entry ![]() , we need to erase the row and the column to which this entry belongs. That is, we need to erase the row
, we need to erase the row and the column to which this entry belongs. That is, we need to erase the row ![]() and the column
and the column ![]() . By doing this, we obtain a submatrix
. By doing this, we obtain a submatrix ![]() defined by
defined by
(2) ![]()
Finally, the minor ![]() is defined as the determinant of this matrix:
is defined as the determinant of this matrix:
(3) ![]()
Here is a complete list of all minors of this matrix
(4) 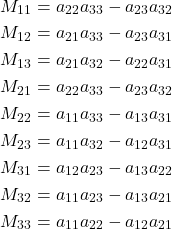
Cofactor of a Matrix
Next, we will define a cofactor of a matrix
DEFINITION OF A COFACTOR OF A MATRIX: The ![]() cofactor of a matrix, denoted by
cofactor of a matrix, denoted by ![]() , is defined by
, is defined by
(5) ![]()
From this definition, we see that the cofactor corresponding to the minor is simply computed as a signed minor. That is, we take the subscripts ![]() of the entry
of the entry ![]() , we add these subscripts together to obtain
, we add these subscripts together to obtain ![]() , and then we compute the sign of the minor as
, and then we compute the sign of the minor as ![]() . The following matrix is filled with the signs of the corresponding minors:
. The following matrix is filled with the signs of the corresponding minors:
(6) 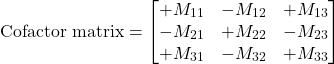
where ![]() is the
is the ![]() minor of the matrix
minor of the matrix ![]() . The matrix cofactors of our 3 by 3 matrix
. The matrix cofactors of our 3 by 3 matrix ![]() are listed below
are listed below
(7) 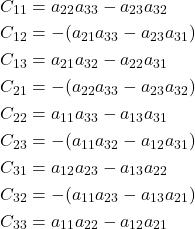
Adjugate Matrix
To define an adjugate matrix of the matrix A, we first need to define a matrix of cofactors. For clarity, we will state the definition for a 3 by 3 matrix. The definitions straightforwardly generalize for matrices of arbitrary dimensions. Consider again the matrix ![]() :
:
(8) 
For such a matrix, we can define the cofactor matrix as follows
(9) 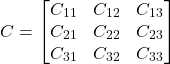
where ![]() is the
is the ![]() cofactor of the matrix
cofactor of the matrix ![]() .
.
DEFINITION OF THE ADJUGATE MATRIX: The adjugate matrix of the matrix ![]() , denoted by
, denoted by ![]() is defined by
is defined by
(10) ![]()
that is, the adjugate matrix of the matrix ![]() is simply computed by transposing the matrix of cofactors. From (9), we have
is simply computed by transposing the matrix of cofactors. From (9), we have
(11) 
Adjugate Matrix and Matrix Inversion
The formula for matrix inversion by using the adjugate matrix is given by
(12) ![]()