In this reinforcement learning tutorial, we introduce state transition probabilities, actions, and rewards and illustrate these important concepts by using the OpenAI Gym Python simulation environment and toolbox. The primary motivation for creating this tutorial comes from the fact that state transition probabilities, actions, and rewards are important concepts in reinforcement learning that in my opinion are not easily understandable concepts for beginners. These concepts should first be explained intuitively by using examples, and only at the second iteration once a student obtains a solid practical understanding, these concepts should be mathematically defined. The YouTube videos accompanying this post are given below.
OpenAI Gym simulation environment is an ideal framework for illustrating these concepts. In this post, we consider the Frozen Lake OpenAI Gym environment and the corresponding reinforcement learning problem. The Frozen Lake problem is illustrated in Fig. 1. below.
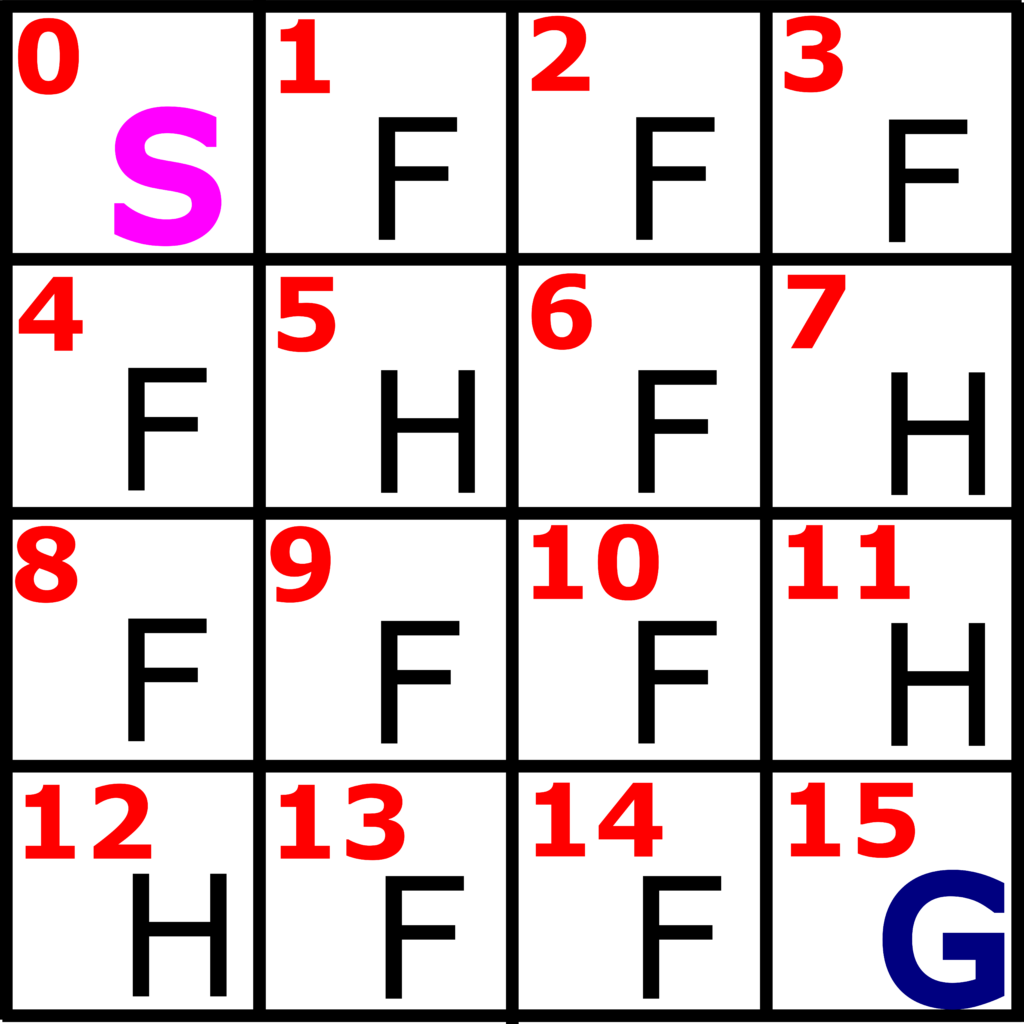
Figure 1 represents a frozen lake. We have in total 16 fields. We start the game at the starting field denoted by “S” and our goal is to reach the goal field, denoted by “G”. The frozen parts of the lake are denoted by “F”. The holes through which we can fall and unsuccessfully end the game are denoted by “H”. Our goal is to reach the goal state “G” by avoiding the hole fields “H” and by only stepping at the frozen fields “F”.
States and Observation Space
The first reinforcement learning concept that we need to introduce is the concept of state. In our case, the states are the fields 0,1,3,4,…, 15, shown in Fig. 1. That is, in total, we have 16 possible states that are enumerated starting from 0 and ending at 15. The observation is a value that is observed from the environment. In our case, the observations are the same as the states (this is not necessarily the case for other problems). Observation space consists of all the possible states starting from 0 until 15.
Episode
The episode represents a series of steps that start from at the initial state 0 or “S”, and that can end either at any of the hole states “H”, in which case we did not win, or in the goal state “G”, in which case we won.
Terminal states
Terminal states are states that terminate an episode. These states in our case are hole states “H” or the goal state “G”.
Actions and Action Space
At every state, except at hole states and goal state, we can perform an action. For example, consider Fig. 2. At the state 6 which represents a frozen field, we can perform 4 actions: UP, DOWN, LEFT, and RIGHT, which are represented by green arrows in Fig. 2.
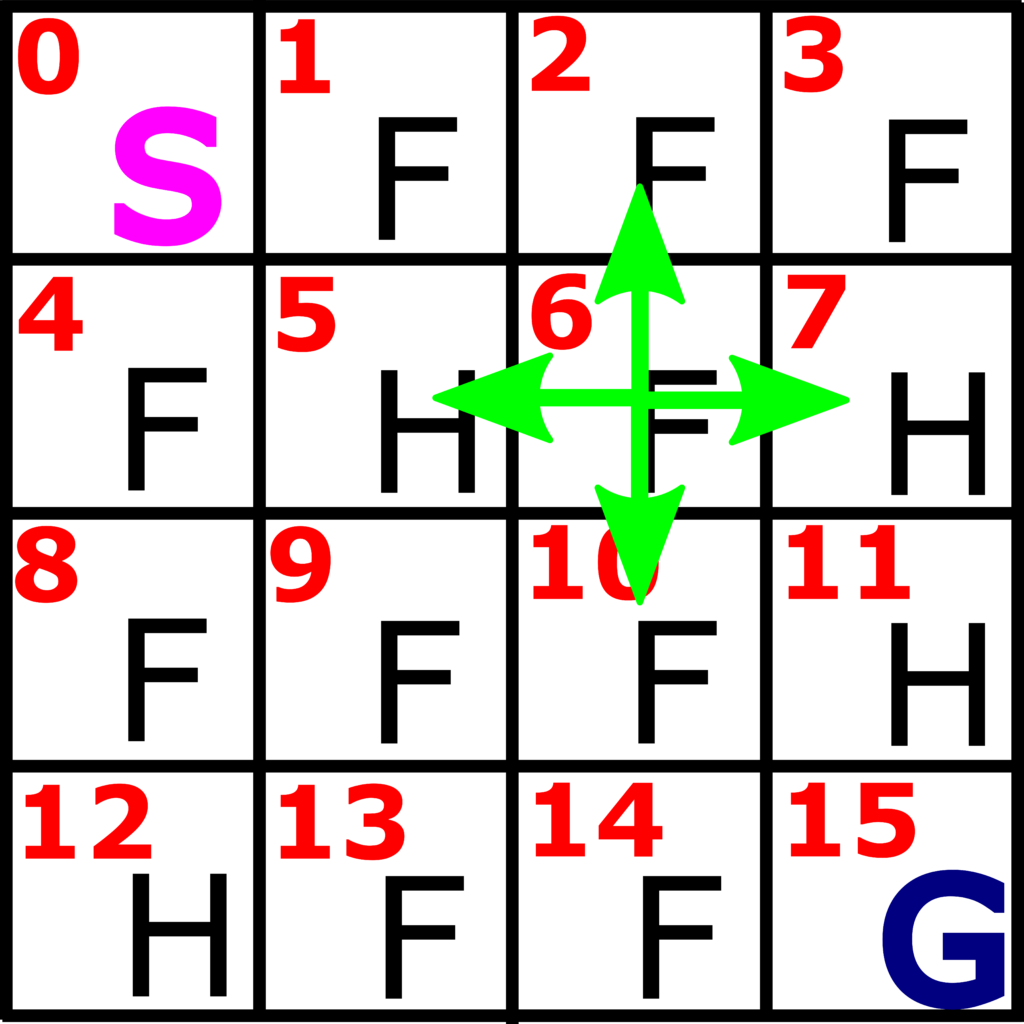
These actions are encoded as follows
- LEFT is encoded by 0.
- DOWN is encoded by 1.
- RIGHT is encoded by 2.
- UP is encoded by 3.
These actions are elements of an action space. That is, the action space consists of 4 actions: 0, 1, 2, and 3, corresponding to LEFT, DOWN, RIGHT, and UP actions.
However, desired actions will not guarantee desired transitions. Here, we should keep in mind that due to the probabilistic nature of environment that will be explained later, certain desired actions at certain states will NOT necessarily lead us to the desired state. For example, let us say that we are at the state 6 and that we perform action DOWN. We expect to go to state 10. However, this will only happen with SOME PROBABILITY. That is, by performing this action, there is some chance that we might end up at some other neighboring state, such as for example, at the state 5. This will be explained later in the text after we introduce transition probabilities.
Rewards
When going from one state to another, we receive a reward after we arrive at the destination state. For example, in Fig. 1, after we arrive at the state 6 from state 2, we receive a reward. The reward can be positive, negative, or zero., Usually, negative rewards are given if our destination state is less favorable. Similarly, more positive rewards are given if the destination states are more positive. It is our own choice how to assign the rewards. In the Frozen Lake example, the rewards are distributed as follows:
- Reach frozen field (F) – obtain the reward of 0.
- Reach hole field (H) – obtain the reward of 0
- Reach goal field (G) – obtain the reward of 1
Of course, we can assign different reward values for these fields. Rewards are important since the reinforcement learning algorithm aims at finding a sequence of actions that maximize the expected sum of rewards. Here, it is important to mention that in the general case, rewards are also not deterministic. This means that the reward obtained by reaching a certain state is not in the general case deterministic. That is, we can also associate a probability with rewards. However, in the Frozen Lake case, the rewards are purely deterministic.
State Transition Probabilities
Finally, we arrive at an important concept of a state transition probability.
Let us explain this important concept through our original example. Consider the following scenario. Let us imagine that we are in state 6, and that we perform action “DOWN”. This is illustrated in Fig. 3. below.
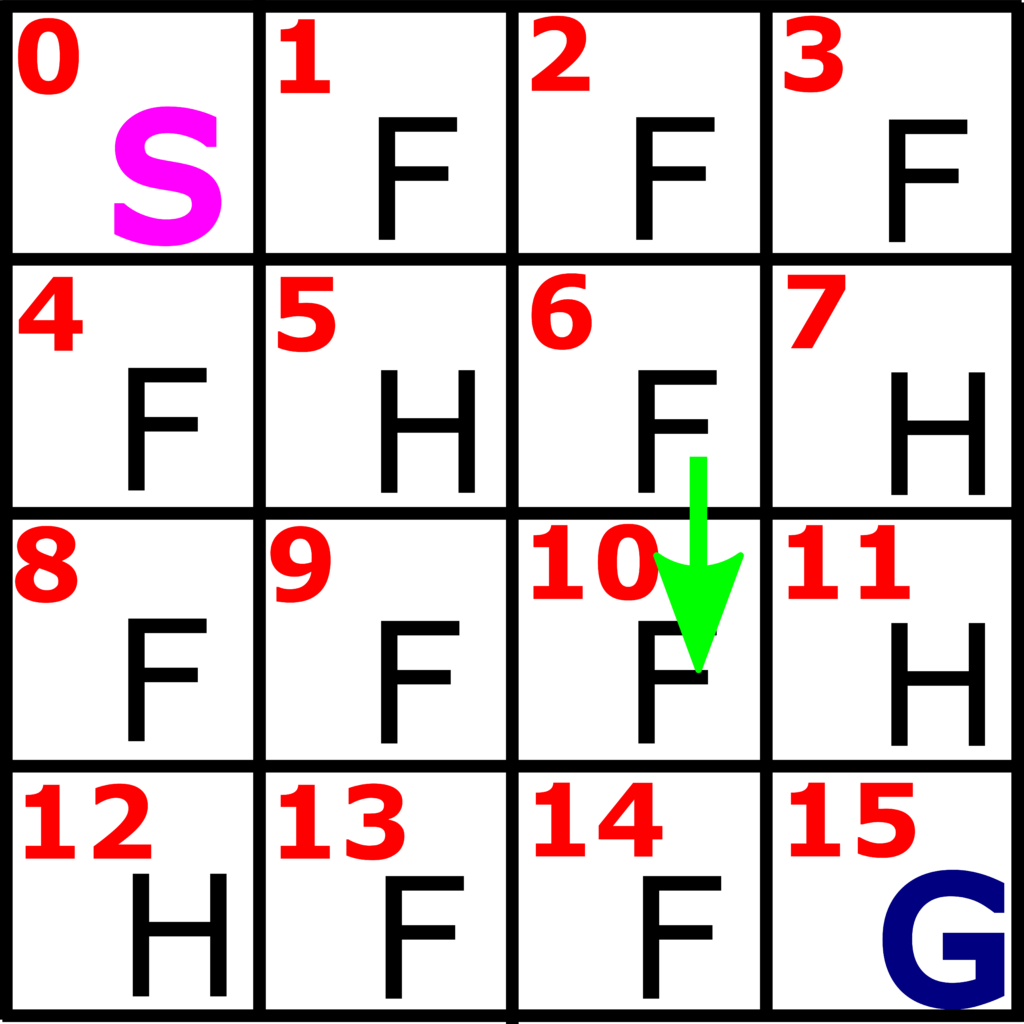
Now, in the purely deterministic case, by applying the action “DOWN” when we are at the state 6, we should arrive at the state 10. However, this is generally not the case. In fact, this will only happen with certain probability. For example with the probability of ![]() . There are also two other scenarios that also have corresponding probabilities. By applying the action “DOWN” in state 6, there is some probability that we might end up at the state 7. For example, this probability can be
. There are also two other scenarios that also have corresponding probabilities. By applying the action “DOWN” in state 6, there is some probability that we might end up at the state 7. For example, this probability can be ![]() . Similarly, by applying the action “DOWN” in state 6, there is some probability that we might end up at the state 5. For example, this probability can be
. Similarly, by applying the action “DOWN” in state 6, there is some probability that we might end up at the state 5. For example, this probability can be ![]() . That is, we have the following three probabilities and scenarios:
. That is, we have the following three probabilities and scenarios:
- We are in state 6, and we apply the action DOWN. The probability of reaching the state 10 is
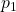 .
. - We are in state 6, and we apply the action DOWN. The probability of reaching the state 7 is
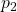 .
. - We are in state 6, and we apply the action DOWN. The probability of reaching the state 5 is
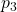 .
.
The probabilities, ![]() and
and ![]() are called the state transition probabilities. They are defined as follows. Let
are called the state transition probabilities. They are defined as follows. Let ![]() be the current discrete-time step and let
be the current discrete-time step and let ![]() be the next time step. Let
be the next time step. Let ![]() be the current state. That is, the state at the current time instant is
be the current state. That is, the state at the current time instant is ![]() Let
Let ![]() be the action performed at the current state
be the action performed at the current state ![]() . That is,
. That is, ![]() . Then the state transition probability of going to state
. Then the state transition probability of going to state ![]() at the time instant
at the time instant ![]() , starting from the state
, starting from the state ![]() and by performing the action
and by performing the action ![]() at the time instant
at the time instant ![]() , is defined by
, is defined by
(1) ![]()
So in our case, we have
(2) 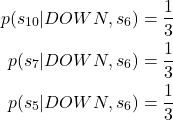
where ![]() and
and ![]() are the states
are the states ![]() ,
, ![]() , and
, and ![]() , and “DOWN” is action. Transition probabilities define how the environment will react when certain actions are performed.
, and “DOWN” is action. Transition probabilities define how the environment will react when certain actions are performed.
Now, that we understand the basic concepts, we can proceed with the Python code and OpenAI Gym library.
First, we install the OpenAI Gym library. This can be done by opening your terminal or the Anaconda terminal and by typing
pip install gym
pip install gym[toy_text]
Next, open your Python Editor. We can import the Gym library, create the Frozen Lake environment, and render the environment. The code is shown below.
import gym
env=gym.make("FrozenLake-v1", render_mode="human")
env.reset()
# render the environment
env.render()
The result is the environment shown below
SFFF
FHFH
FFFH
HFFG
or in the rendered window that is shown in the figure below
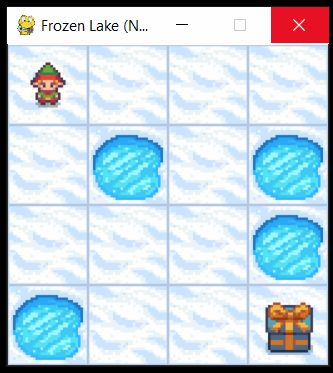
Information about the observation and action spaces can be obtained by executing these code lines
# observation space - states
env.observation_space
# actions: left -0, down - 1, right - 2, up- 3
env.action_space
Let us now generate random actions, perform a random step, and render the environment.
#generate random action
randomAction= env.action_space.sample()
returnValue = env.step(randomAction)
# format of returnValue is (observation,reward, terminated, truncated, info)
# observation (object) - observed state
# reward (float) - reward that is the result of taking the action
# terminated (bool) - is it a terminal state
# truncated (bool) - it is not important in our case
# info (dictionary) - in our case transition probability
env.render()
Here are a few important comments about these code lines. The function “env.action_space.sample()” samples a random action from the action space ![]() . Then, the function “env.step(randomAction)” performs the generated step, and returns the value. The returned value has the following form
. Then, the function “env.step(randomAction)” performs the generated step, and returns the value. The returned value has the following form
(observation,reward, terminated, truncated, info)
In our case, we obtained
(0, 0.0, False, False, {‘prob’: 0.3333333333333333})
This means that the final state is 0, reward is 0, “False” means that the final state is not a terminal state (we did not arrive at the hole or the goal state), another Boolean return value “False” is not important for this discussion, and {‘prob’: 0.3333333333333333} is the transition probability from our initial state 0 to state 0.
We can also perform deterministic actions by directly specifying the action
# perform deterministic step 0,1,2,3
returnValue = env.step(1)
We can reset the environment, or we can return it to the original state by typing
# reset the environment
env.reset()
By executing the code on your computer, you might notice that when applying the action 1, that is the action “DOWN”, you will not always transition to the state below the current state. This is because the actual response of the environment is dictated by the transition probabilities. The transition probabilities can be accessed by typing env.P[state][action]. env.P is actually a dictionary containing all the transition probabilities. The following code lines illustrate transition probabilities:
#transition probabilities
#p(s'|s,a) probability of going to state s'
# starting from the state s and by applying the action a
# env.P[state][action]
env.P[0][1] #state 0, action 1
# output is a list having the following entries
# (transition probability, next state, reward, Is terminal state?)
The output of
env.P[0][1] #state 0, action 1
is
[(0.3333333333333333, 0, 0.0, False),
(0.3333333333333333, 4, 0.0, False),
(0.3333333333333333, 1, 0.0, False)]
This output should be interpreted as follows
(transition probability, next state, reward, Is terminal state?)
That is
- Transition probability from state 0 and under action 1 (DOWN) to state 0 is 1/3, obtained reward is 0, and the state 0 (final state) is not a terminal state.
- Transition probability from state 0 and under action 1 (DOWN) to state 4 is 1/3, obtained reward is 0, and the state 4 (final state) is not a terminal state.
- Transition probability from state 0 and under action 1 (DOWN) to state 1 is 1/3, obtained reward is 0, and the state 1 (final state) is not a terminal state.
Let us now see the transition probability env.P[6][1]
env.P[6][1]
The result is
[(0.3333333333333333, 5, 0.0, True),
(0.3333333333333333, 10, 0.0, False),
(0.3333333333333333, 7, 0.0, True)]
That is
- Transition probability from state 6 and under action 1 (DOWN) to state 5 is 1/3, the obtained reward is 0, and the state 5 (final state) is a terminal state.
- Transition probability from state 6 and under action 1 (DOWN) to state 10 is 1/3, obtained reward is 0, and the state 10 (final state) is not a terminal state.
- Transition probability from state 6 and under action 1 (DOWN) to state 7 is 1/3, obtained reward is 0, and the state 7 (final state) is a terminal state.