In this post, we explain:
- How to derive rotation matrices
- How to transform vectors between two rotated coordinate systems.
A YouTube video accompanying this post is given below.
Rotation matrices are important for modeling robotic systems and for solving a number of problems in robotics.
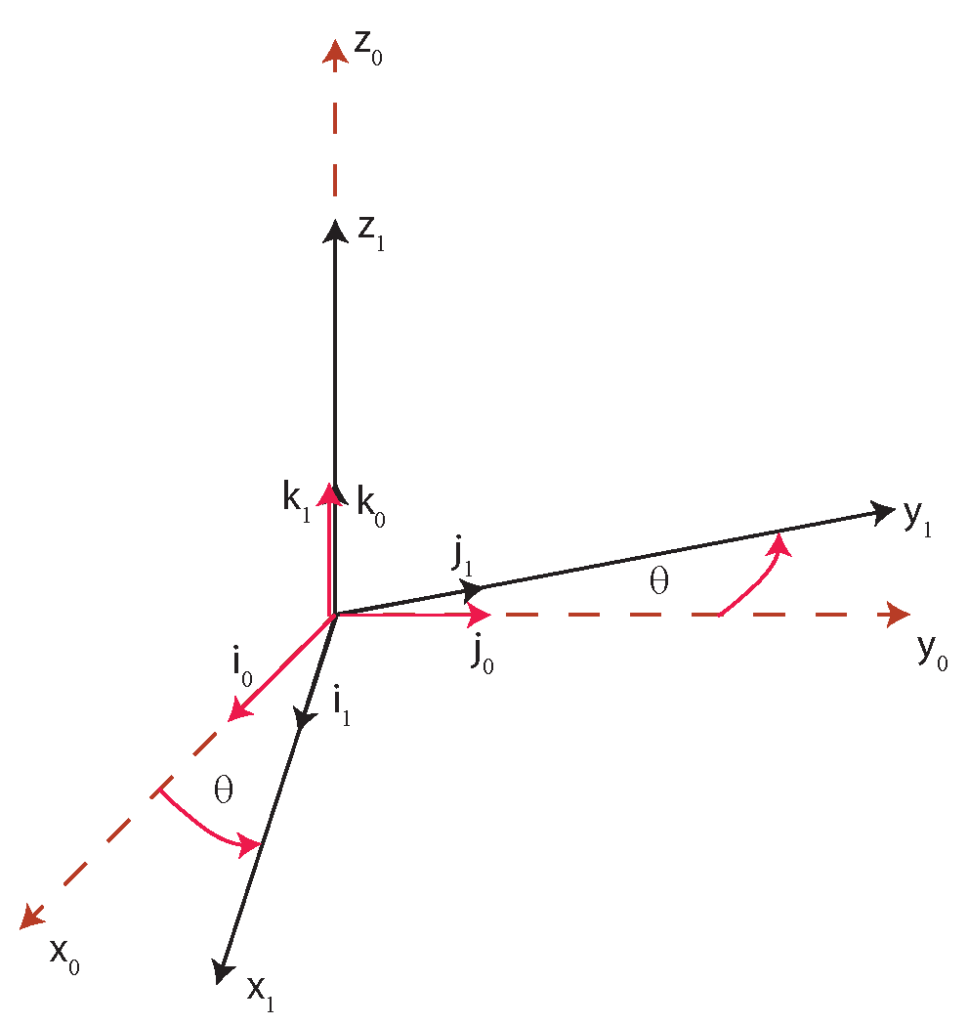
Consider Fig. 1 below.
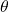 around the
around the 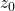 axis.
axis.We have two coordinate systems. The coordinate system ![]() is fixed. This coordinate system is called the inertial or reference coordinate system. Note that in robotics, coordinate systems are also called frames. The coordinate system
is fixed. This coordinate system is called the inertial or reference coordinate system. Note that in robotics, coordinate systems are also called frames. The coordinate system ![]() is rotated for the angle
is rotated for the angle ![]() with respect to the coordinate system
with respect to the coordinate system ![]() around the
around the ![]() axis. The vectors
axis. The vectors ![]() ,
, ![]() , and
, and ![]() are the unit vectors of the coordinate axes
are the unit vectors of the coordinate axes ![]() ,
, ![]() , and
, and ![]() . On the other hand, the vectors
. On the other hand, the vectors ![]() ,
, ![]() , and
, and ![]() are the unit vectors of the coordinate axes
are the unit vectors of the coordinate axes ![]() ,
, ![]() , and
, and ![]() .
.
Consider the vector ![]() that rotates together with the frame
that rotates together with the frame ![]() and that is fixed with respect to this frame. This vector is shown in the figure below.
and that is fixed with respect to this frame. This vector is shown in the figure below.
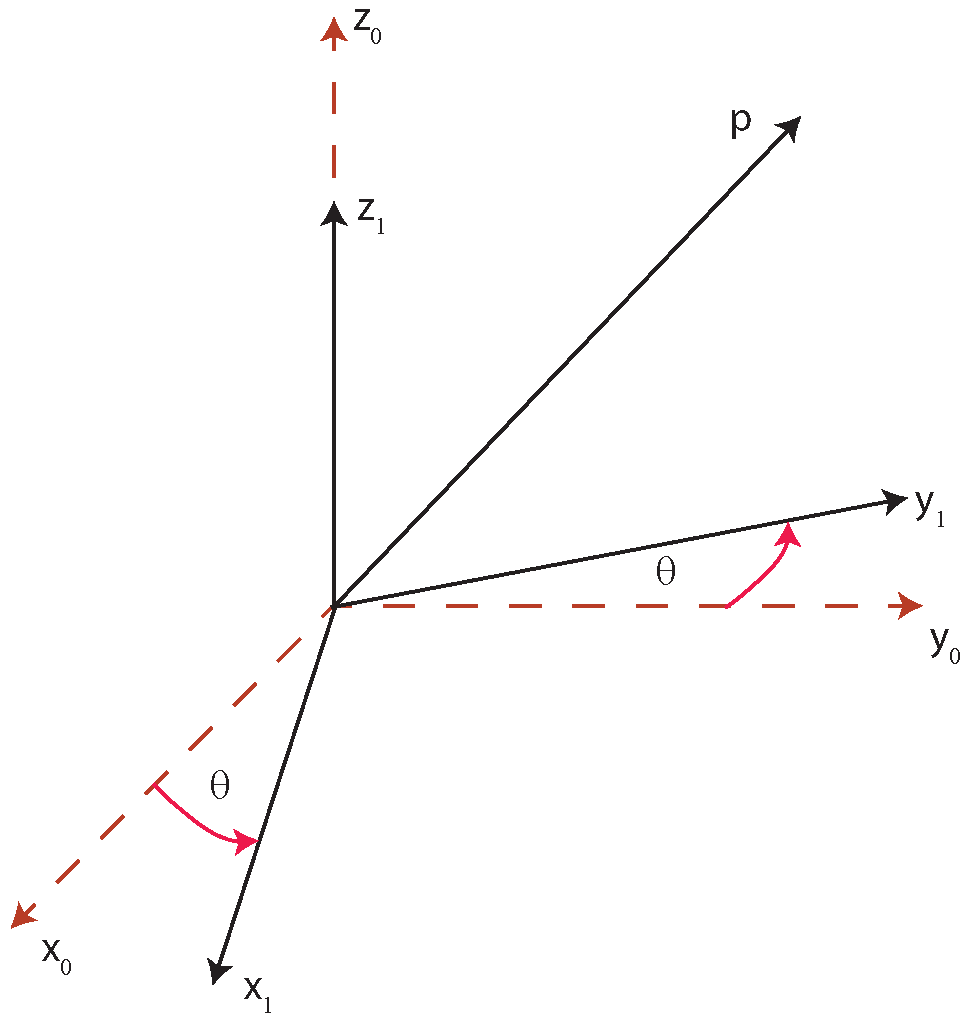
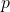 rotating together with the frame
rotating together with the frame 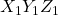 .
.Problem: Knowing the coordinates of the vector ![]() in the frame
in the frame ![]() , and the angle of rotation
, and the angle of rotation ![]() , represent this vector in the frame
, represent this vector in the frame ![]() .
.
The representation of the vector ![]() in the frame
in the frame ![]() is
is
(1) ![]()
where the notation ![]() stands for the representation of the vector
stands for the representation of the vector ![]() in the frame
in the frame ![]() . And the scalars
. And the scalars ![]() ,
, ![]() , and
, and ![]() are the projections. We want to compute this representation of the vector
are the projections. We want to compute this representation of the vector ![]() in the frame
in the frame ![]()
(2) ![]()
(3) 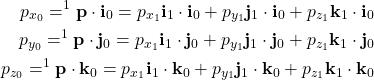
where the notation ![]() is used to denote the scalar product between vectors. The last equation can be represented in the vector form
is used to denote the scalar product between vectors. The last equation can be represented in the vector form
(4) 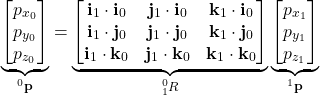
where
(5) 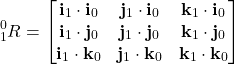
is the rotation matrix. The notation ![]() denotes the transformation from the frame
denotes the transformation from the frame ![]() (subscript) to the frame
(subscript) to the frame ![]() (superscript). The first column of the rotation matrix is the projection of the vector
(superscript). The first column of the rotation matrix is the projection of the vector ![]() onto the axes of the frame
onto the axes of the frame ![]() . The second column of the rotation matrix is the projection of the vector
. The second column of the rotation matrix is the projection of the vector ![]() onto the axes of the frame
onto the axes of the frame ![]() . The third column of the rotation matrix is the projection of the vector
. The third column of the rotation matrix is the projection of the vector ![]() onto the axes of the frame
onto the axes of the frame ![]() .
.
Now, consider Fig.1 again. Since ![]() and
and ![]() are the unit vectors, we have
are the unit vectors, we have ![]() . That is,
. That is, ![]() is the projection of the vector
is the projection of the vector ![]() onto the vector
onto the vector ![]() , and
, and ![]() is the angle between these two vectors. By using this method, we can populate the rotation matrix as follows:
is the angle between these two vectors. By using this method, we can populate the rotation matrix as follows:
(6) 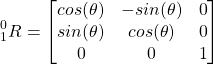
Rotation matrices have the following nice property:
(7) ![]()
That is, they are orthonormal. The inverse of ![]() is actually a transformation from the frame
is actually a transformation from the frame ![]() to the frame
to the frame ![]() , to see this, multiply the equation (4) by
, to see this, multiply the equation (4) by ![]() :
:
(8) ![]()
That is, ![]() .
.