In this mathematics, linear algebra, and control engineering tutorial, we explain how to calculate eigenvalues and eigenvectors of matrices by hand. This tutorial is very important for control engineers and people studying the stability of dynamical systems. The YouTube video accompanying this post is given below.
Problem Formulation: Consider the 2 by 2 matrix ![]() defined below.
defined below.
(1) ![]()
Calculate by hand the eigenvalues and eigenvectors of this matrix.
To solve this problem, first, we need to recall the definition of the eigenvalues and eigenvectors. The eigenvalue ![]() and the eigenvector
and the eigenvector ![]() of the matrix
of the matrix ![]() are defined and related by the following equation
are defined and related by the following equation
(2) ![]()
From the last equation, we have
(3) ![]()
and finally
(4) ![]()
For the fixed eigenvalue ![]() , the equation in (4) represents a linear system of equations, where the variables that we want to solve for are the entries of the eigenvector
, the equation in (4) represents a linear system of equations, where the variables that we want to solve for are the entries of the eigenvector ![]() . This system always has a trivial solution
. This system always has a trivial solution ![]() (all entries of
(all entries of ![]() are zero). However, we are not interested in a trivial solution. Instead, we are interested in a nontrivial solution. A nontrivial solution is a solution
are zero). However, we are not interested in a trivial solution. Instead, we are interested in a nontrivial solution. A nontrivial solution is a solution ![]() , where at least one entry of
, where at least one entry of ![]() is not equal to zero. We are searching for nontrivial solutions.
is not equal to zero. We are searching for nontrivial solutions.
The main condition for the existence of the nontrivial solution is
(5) ![]()
where ![]() is the identity matrix, and
is the identity matrix, and ![]() is the matrix determinant operator. The equation (5) is a polynomial in
is the matrix determinant operator. The equation (5) is a polynomial in ![]() . In fact, the polynomial
. In fact, the polynomial
(6) ![]()
is called the characteristic polynomial. The eigenvalues are determined as zeros of the characteristic polynomial, that is, as the solutions of (5). To summarize
- The eigenvalues
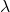 are determined as zeros of the characteristic polynomial, that is, as the solutions of (5).
are determined as zeros of the characteristic polynomial, that is, as the solutions of (5). - For the computed value of
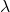 obtained by solving (5), the corresponding eigenvector is obtained by solving
obtained by solving (5), the corresponding eigenvector is obtained by solving (7)
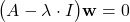
for .
.
Next, let us apply this theory to our problem. We first need to compute the zeros of the characteristic polynomial:
(8) 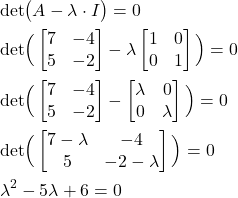
The zeros of the characteristic polynomial are found by computing the zeros of the last equation. To compute the zeros (eigenvalues), we use the equation for zeros of a quadratic equation. The eigenvalues are
(9) ![]()
For these two eigenvalues, we need to compute the corresponding eigenvectors. The eigenvectors are computed by solving the corresponding systems of homogeneous equations (7). For ![]() , we have
, we have
(10) 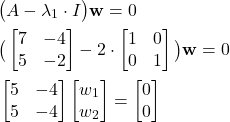
where ![]() and
and ![]() are the entries of
are the entries of ![]() . From the last equation, we have
. From the last equation, we have
(11) ![]()
This is actually a single equation:
(12) ![]()
From this equation, we have
(13) ![]()
and ![]() can be freely selected. That is, there are an infinite number of eigenvectors for the eigenvalue
can be freely selected. That is, there are an infinite number of eigenvectors for the eigenvalue ![]() . These eigenvectors are parametrized as follows
. These eigenvectors are parametrized as follows
(14) ![]()
where ![]() is a real parameter that can take any value.
is a real parameter that can take any value.
Next, we determine the eigenvectors for ![]() . We have
. We have
(15) 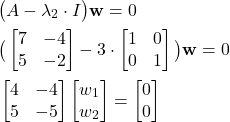
From the last equation, we have
(16) ![]()
By dividing the first equation by ![]() and the last equation by
and the last equation by ![]() , we obtain
, we obtain
(17) ![]()
These two equations are actually a single equation that looks like this
(18) ![]()
From this equation, we obtain
(19) ![]()
where ![]() can freely be selected. This means that there are an infinite number of eigenvectors of the matrix
can freely be selected. This means that there are an infinite number of eigenvectors of the matrix ![]() . These eigenvectors are parameterized by the following equation
. These eigenvectors are parameterized by the following equation
(20) ![]()
where ![]() is a real number that can take any value in the real set.
is a real number that can take any value in the real set.