Homework Assignment 4 – Fusion of Engineering, Control, Coding, Machine Learning, and Science

Consider the beam supported at supports A and B that is shown in the figure below. There is a distributed load of $50,000$ $N/m$ acting on top of it. Assume that the beam is made of structural steel (standard material option in Fusion360). Good luck!

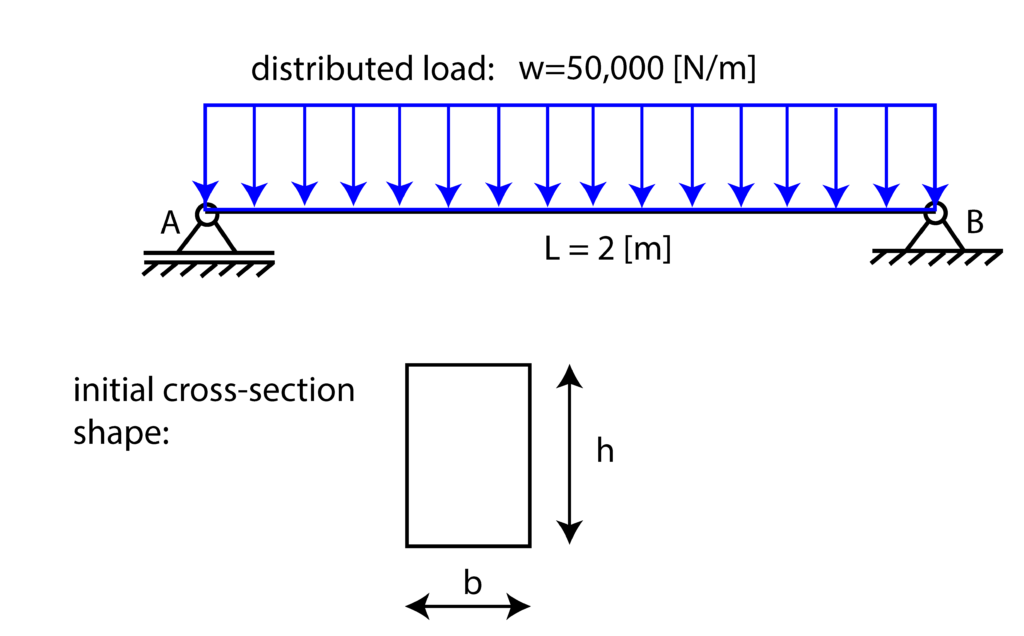
Perform the following steps

Compute the reaction forces, and determine internal force and internal moment diagrams.
Find the maximum value of the moment diagram.
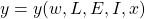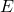Derive the general form of the equation that describes the deformation in the vertical direction. That is, determine $y=y(w,L,E,I,x)$ , where $w$ is the distributed load, $L$ is the length, $E$ is the modulus of elasticity, and 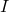$I$ is the moment of inertia. Determine the solution by solving the differential equation describing the beam deformation.
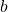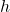Determine the cross-section dimensions $b$ and $h$ such that the beam can safely withstand the applied distributed load. Hint: To solve this question, you will need the answer obtained in question 2.
For the dimensions found in question 4, simulate the deformation in Fusion 360. Verify that the analytical solution in question 4 is correct by comparing the analytical solution with the maximal simulated deformation obtained by Fusion 360. Hint: to solve this problem, you will need to generate a graph in MATLAB that plots 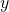$y$ as the function of 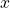$x$ (the function 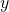$y$ in question 3). From this graph you read the deformation, and then you can compare this deformation with Fusion 360.
Verify the accuracy of the solution of question 3, by comparing the Fusion 360 deformation with the deformation predicted by the equation derived in question 3.
Optimize the shape of the beam such that the mass is reduced. However, make sure that the optimized shape should be able to withstand the applied load.
(requires independent investigation) Learn how to compute the reaction forces in Fusion 360 (watch videos and search the Internet). Compare the results with the analytical results obtained by solving question 1.