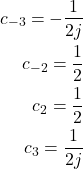In this mathematics, calculus, signal processing, and control engineering tutorial, we will learn how to express ![]() and
and ![]() functions of the real argument or of the real angles as the sum and difference of complex exponentials. That is, we will learn how to derive the following formulas
functions of the real argument or of the real angles as the sum and difference of complex exponentials. That is, we will learn how to derive the following formulas
(1) 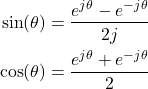
where ![]() is the imaginary unit and
is the imaginary unit and ![]() is the angle that is often expressed in radians. These two formulas play a very important role in digital signal processing, control engineering, and in many other fields because many times they can be used to significantly simplify calculations of quantities such as transfer functions, magnitude and phase responses, etc. In this tutorial, we explain how to derive these formulas, and at the end of the tutorial, we explain how these formulas can be used to compute the coefficients of the Fourier series Expansion. The YouTube video accompanying this post is given below.
is the angle that is often expressed in radians. These two formulas play a very important role in digital signal processing, control engineering, and in many other fields because many times they can be used to significantly simplify calculations of quantities such as transfer functions, magnitude and phase responses, etc. In this tutorial, we explain how to derive these formulas, and at the end of the tutorial, we explain how these formulas can be used to compute the coefficients of the Fourier series Expansion. The YouTube video accompanying this post is given below.
Derivation of Formulas
To derive these formulas we need to start from the Euler representation of the exponential of the complex number. Consider the complex unit circle shown in the figure below.
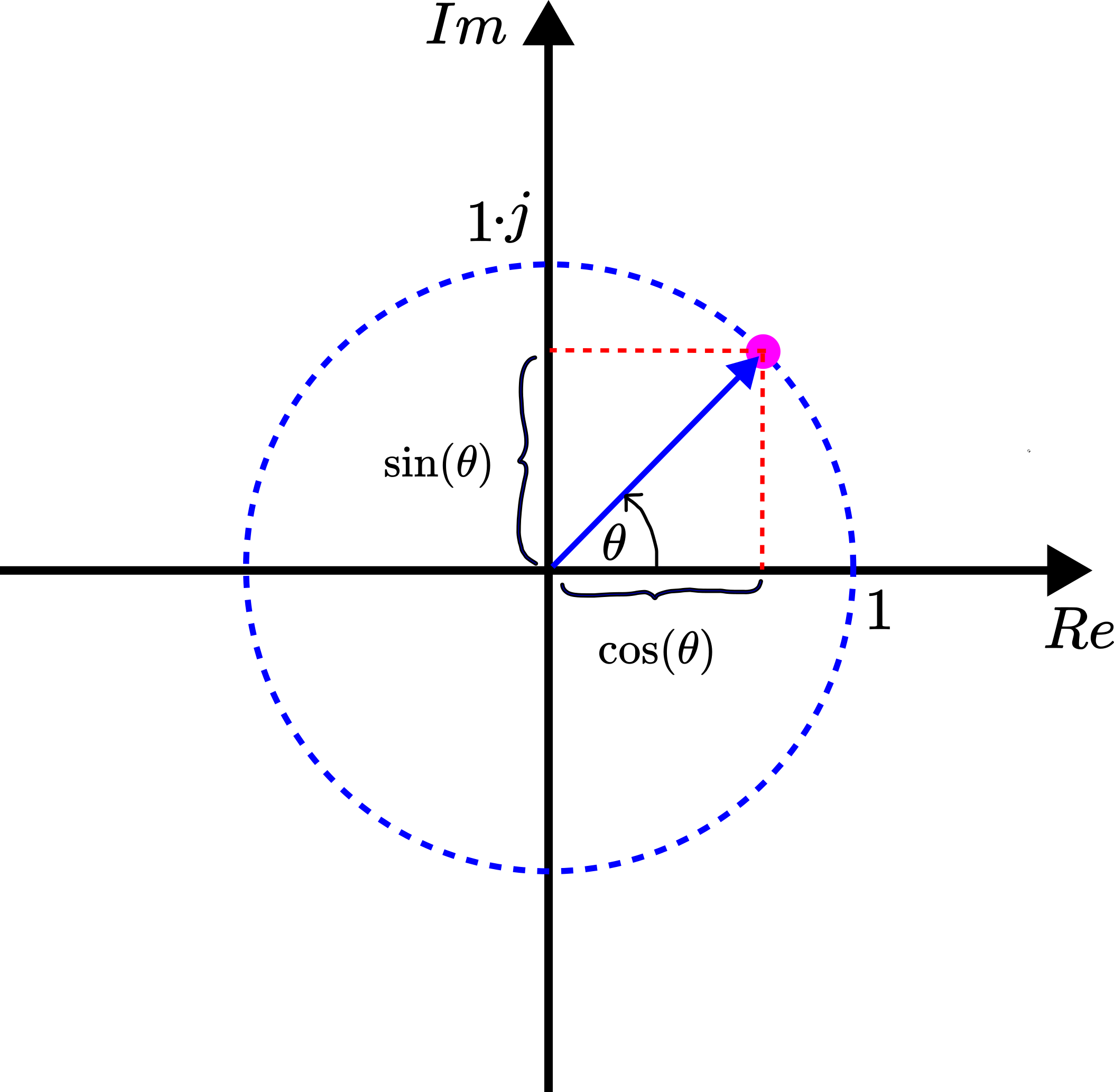
The complex number shown in the figure above can be represented in the polar form as
(2) ![]()
The complex number has projections onto the real and imaginary axes. These projections are ![]() , and
, and ![]() , respectively. Consequently, we can represent the polar form as
, respectively. Consequently, we can represent the polar form as
(3) ![]()
This is Euler’s formula for the exponential of the complex number. On the other hand, from (3), we have
(4) ![]()
Let us write the formulas (3) and (4) together
(5) 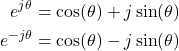
To derive the formulas for ![]() and
and ![]() , we can think of these two equations as two equations with two unknowns that we want to solve. The unknowns are
, we can think of these two equations as two equations with two unknowns that we want to solve. The unknowns are ![]() and
and ![]() .
.
Let us first solve these two equations for ![]() . From (5), we have
. From (5), we have
(6) ![]()
From the last equation, we obtain the expression for ![]()
(7) ![]()
Next, let us solve the equations (5) for ![]() . From this equation, we have
. From this equation, we have
(8) ![]()
From the last equation, we obtain the expression for ![]()
(9) ![]()
Application of Derived Formulas
We use the derived formulas to solve the following problem. Compute the Fourier series coefficients and Fourier series expansion of the following periodic function
(10) ![]()
where ![]() is the fundamental frequency. We can solve this problem by using the Fourier series integrals that we explained in our previous tutorial. However, there is a more elegant approach to solving this problem by using the formulas (1). By using these formulas, we obtain
is the fundamental frequency. We can solve this problem by using the Fourier series integrals that we explained in our previous tutorial. However, there is a more elegant approach to solving this problem by using the formulas (1). By using these formulas, we obtain
(11) ![]()
From this expression, we immediately obtain the Fourier series expansion
(12) ![]()
That is
(13) ![]()
where the Fourier series coefficients are given below
(14)