In this post, we present a simple experimental setup for estimating the gravitational acceleration constant. The gravitational acceleration is estimated using a least-squares method. The data acquisition and computations are performed using a Raspberry Pi (RP) microcontroller. A video about this post is given below.
The working principle of the experimental setup is shown in Fig.1 below.
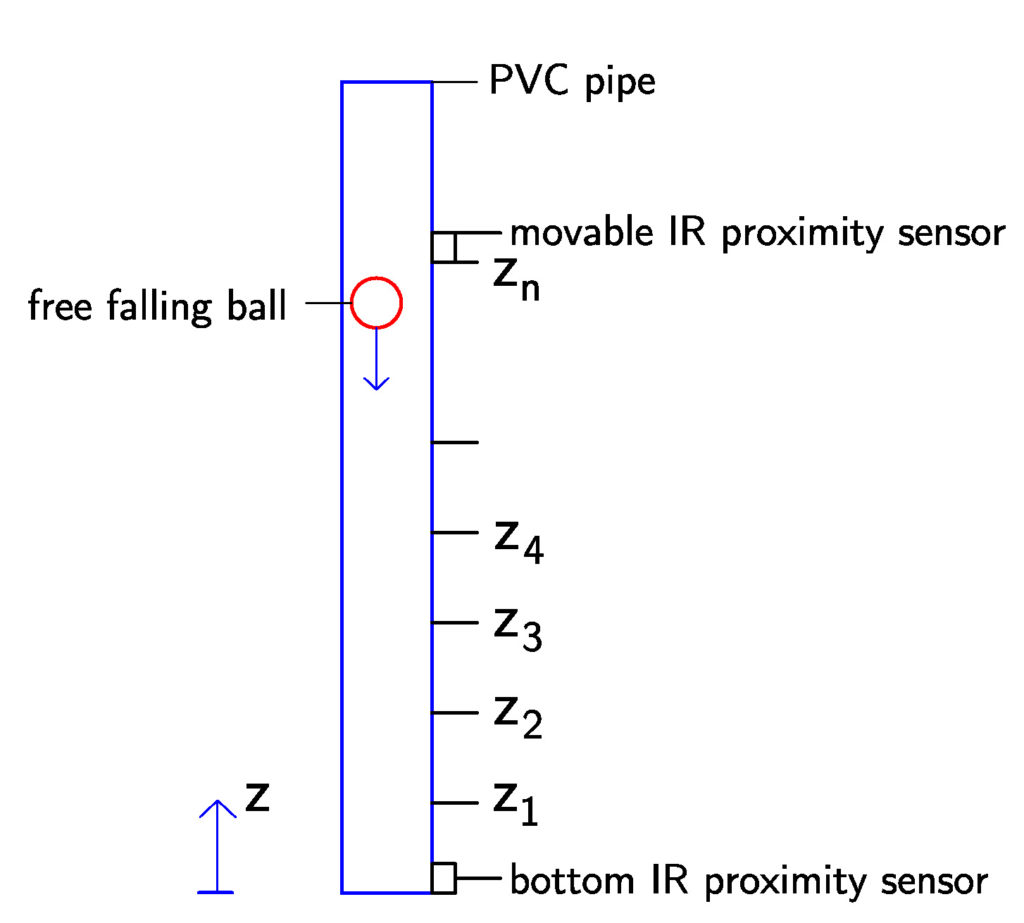
A (tennis) ball freely falls in a PVC pipe. The PVC pipe has ball openings and sensor mounts at prescribed heights ![]() ,
, ![]() . At the bottom of the pipe, an InfraRed (IR) proximity sensor is mounted. We use OSOYOO low-cost IR proximity sensors whose specs can be found here. The sensor output is a digital signal (HIGH or LOW voltage) depending on the proximity of the object. Another IR proximity sensor is placed at prescribed heights
. At the bottom of the pipe, an InfraRed (IR) proximity sensor is mounted. We use OSOYOO low-cost IR proximity sensors whose specs can be found here. The sensor output is a digital signal (HIGH or LOW voltage) depending on the proximity of the object. Another IR proximity sensor is placed at prescribed heights ![]() . Using an RP microcontroller we measure the time between the activations of the upper and lower sensors. This time, denoted by
. Using an RP microcontroller we measure the time between the activations of the upper and lower sensors. This time, denoted by ![]() , is approximately equal to the time it takes for the ball to fall from the height
, is approximately equal to the time it takes for the ball to fall from the height ![]() .
.
The estimation problem can be formulated as follows. From the set of measurements ![]() , estimate the gravitational acceleration constant.
, estimate the gravitational acceleration constant.
Next, we derive the equation of motion of the free-falling ball. The second Newton’s law governs the motion of the ball:
(1) ![]()
or
(2) ![]()
where
(3) ![]()
By integrating this equation two times, and by taking into account the initial condition
(4) ![]()
where
(5) ![]()
This equation can be used to form the least-squares problem for estimating the constant
(6) 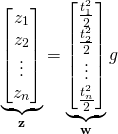
where
(7) ![]()
where
(8) ![]()
where ![]() denotes the 2-norm.
denotes the 2-norm.
The solution is given by:
(9) ![]()
where
The MATLAB code for calculating the g constant is given below.
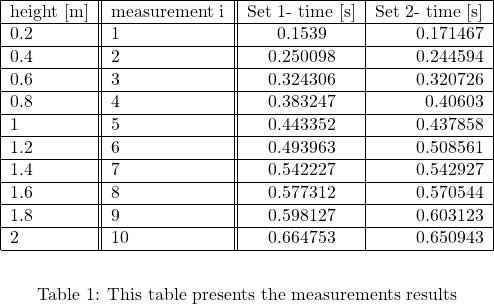
g_true=9.80665;
data=[0.2 1 0.1539 0.171467;
0.4 2 0.250098 0.244594;
0.6 3 0.324306 0.320726;
0.8 4 0.383247 0.40603 ;
1 5 0.443352 0.437858;
1.2 6 0.493963 0.508561;
1.4 7 0.542227 0.542927;
1.6 8 0.577312 0.570544;
1.8 9 0.598127 0.603123;
2 10 0.664753 0.650943;];
w_est=data(:,3).^2/2;
w_val=data(:,4).^2/2;
z =data(:,1)+0.01;
g=inv(w_est'*w_est)*(w_est'*z)
error=((g_true-g)/g_true)*100
The estimation error is 0.5 %. Notice that on line 16 we added an additional centimeter to the height vector. This is has been done to take into account the fact that the sensors are placed 1cm below the point from which the ball falls (for more details see the video). The C/C++ code for obtaining the measurements is given below.
/*
/ Andrew Brennan
/ Nicholas Doherty
/ Prof. Aleksandar Haber, PhD
/ Verifying Earth's Gravitational Acceleration
/ CUNY College of Staten Island
/ 6/19/2019
/
*/
#include <wiringPi.h>
#include <iostream>
#include <ctime>
using namespace std;
int main(void)
{
clock_t startTime;
clock_t endTime;
double duration = 0;
int sensor_upper_pin = 0; // Set upper sensor pin.
int sensor_lower_pin = 2;// Set lower sensor pin.
int sensor_upper = 0;
int sensor_lower = 0;
int iteration_num = 0;
wiringPiSetup();
pinMode(sensor_upper_pin, INPUT); // Set upper sensor to input.
pinMode(sensor_lower_pin, INPUT); // Set lower sensor to input.
while(1)
{
sensor_upper = digitalRead(sensor_upper_pin); // Continually check upper sensor for input.
if (sensor_upper == 0) // When ball passes upper sensor,
{
startTime = clock(); // start clock.
sensor_lower = digitalRead(sensor_lower_pin); // Continually check lower sensor for input.
while (sensor_lower == 1) // While no input from lower sensor.
{
sensor_lower = digitalRead(sensor_lower_pin); // Do nothing.
}
endTime = clock(); // Stop clock when ball passes lower sensor.
duration = (endTime - startTime) / (double) CLOCKS_PER_SEC; // Calculate time difference between readings.
iteration_num++;
cout<<"\nIteration "<<iteration_num<<".\nTime between sensor detections: "<<duration<<" seconds."<<endl; // Output duration.
}
}
return 0;
}
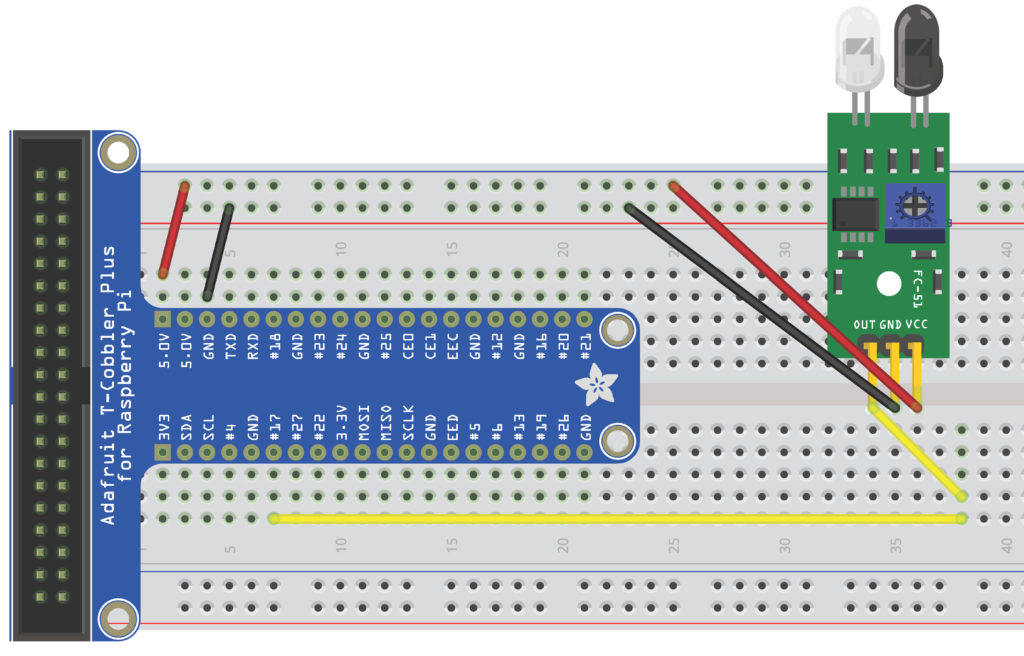
The wiring diagram for one sensor is shown below. Notice that that the power pin of the sensor should be attached to the external power supply.