ENS100- Exam – Fusion of Engineering, Control, Coding, Machine Learning, and Science

General remarks

You need to explain the complete procedure that you used to solve the problem. Final answers without the explained procedure will count 0 points.
Please do not cheat on the exam or ask someone else to complete the assignment for you. We can easily identify students that did not do the exam independently.
When submitting the assignment, follow the following guidelines. If you write the exam on sheets of paper, scan or take photos of all the pages. Then, transfer the photos to your computer. Then, open a new Microsoft Word file (or open a file in the text processor that you use) and copy and paste all the photos. On the first page of the Word document, write your name and the student identification number (employee ID number). Save the Word file as “yourname_yoursurname”. For example, if a person’s name is John Doe, the name of the file should be “john_doe”. Send the file as a single attachment to my email address. You can also save the file in the pdf file form. If you have a digital writing pad, you can also use the pad. In that case, you still need to combine the digital pages of your exam in a single file.
I will not accept submissions after 3 PM on November 10, 2020. Submit your exam before 3PM.
On November 12, 2020, you will defend your exam online. I will ask you a few simple questions to verify that you did the exam independently. If you successfully answer these questions I will grade your report.

Question 1 (10 points). Transform units.

(1) $\begin{align*}15 \frac{[miles]}{[hour]} \;\; \text{to} \;\; \frac{[centimeter]}{[second]} \\100 [kilograms] \;\; \text{to} \;\; [pounds] \\15 \frac{[kilometers]}{[day]} \;\; \text{to} \;\; \frac{[milimiter]}{[second]} \\10 \frac{[meters]}{[minute]} \;\; \text{to} \;\; \frac{[miles]}{[seconds]}\end{align*}$

Question 2 (10 points). Interest rates.
Initially, you borrowed $$10,000$ from a bank. If the monthly interest rate is $2\%$ , calculate the amount that you will have to return to the bank after 2 years.

Question 3 (10 points). Function graphs.
Sketch the graphs of the following functions (on separate graphs)

(2) $\begin{align*}y=2x-5 \\y=x^2-5 \\y=x^2-2x+1\end{align*}$

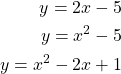
Question 4 (10 points). Quadratic equations.
Compute the solutions of quadratic equations

(3) $\begin{align*}x^2+5x-6=0 \\x^2+x-6=0 \\x^2-1=0 \\x^2+1=0\end{align*}$

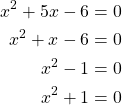
Question 5 (10 points). Function intersection.
Sketch the following two functions and compute their intersection points

(4) $\begin{align*}y=2x-1 \\y=x^{2}-1\end{align*}$

Question 6 (10 points). Vector projections
Vectors in a) and b) are defined by the magnitude (number) and the angle. Calculate x and y projections of the vectors.

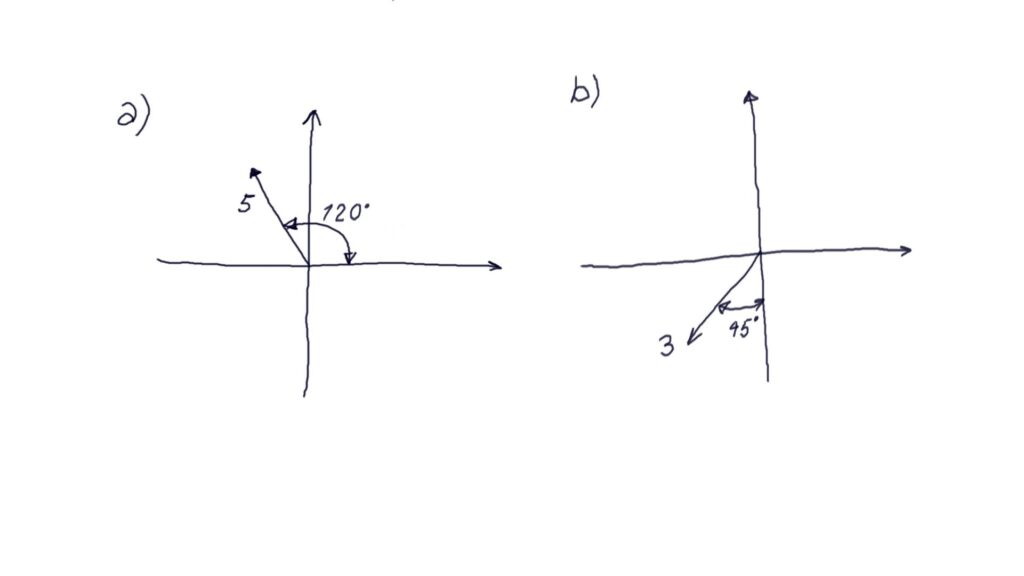
Question 7 (10 points) Velocity and acceleration
An object is moving along a straight line. Its position that is a function of time is given by the following table.

Rendered by QuickLaTeX.com

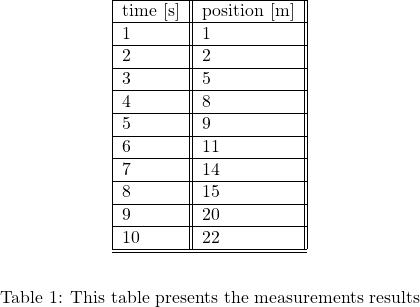
Estimate
a) Velocity at the time instant $4 [s]$
b) Velocity at the time instant $5 [s]$
c) Acceleration at the time instant $4 [s]$

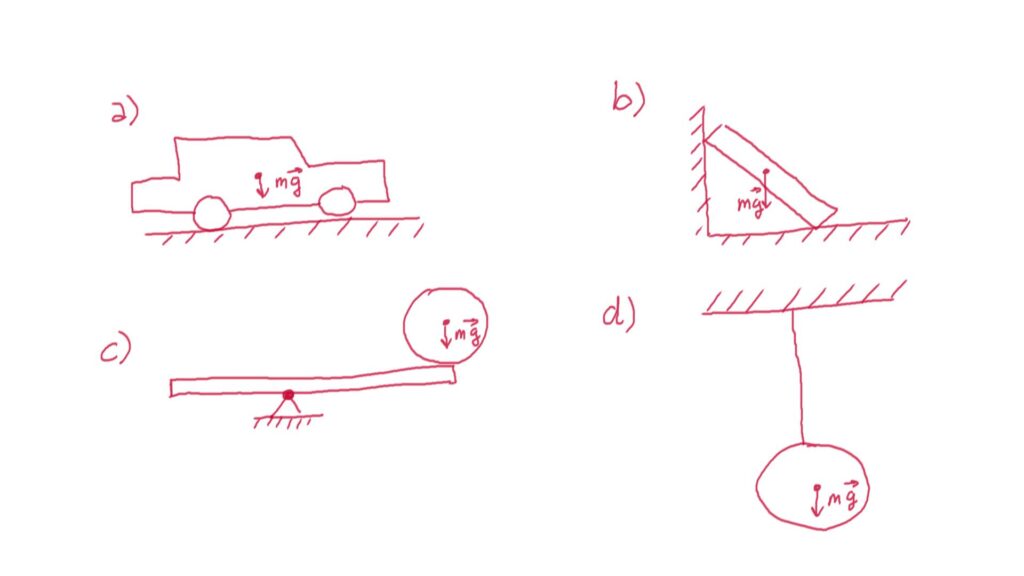
Question 8 (10 points) Free body diagram

a) free body diagram of the car
b) free body diagram of the bar
c) free body diagram of the ball and the bar
d) free body diagram of the ball and the hanging cord

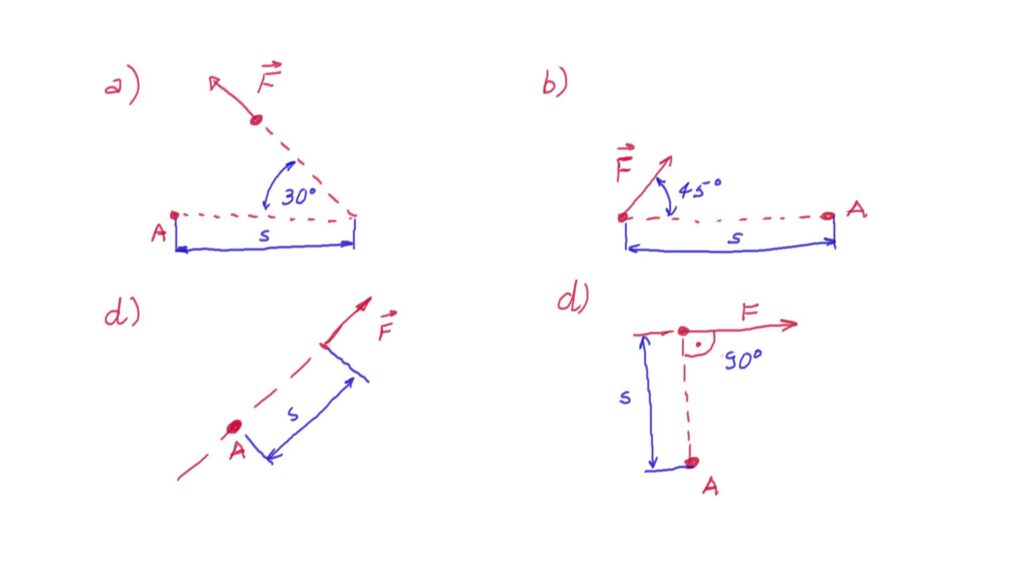
Question 9 (10 points). Moment of the force.

Given the force $F$ , angle, and distance $s$ , compute the moment of the force $F$ with respect to the point A for the cases given in the panels of the figure below.