Deformation, Strain, and Hooke’s law – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this lecture, we will introduce very important concepts. We will explain the concepts of axial deformation, axial strain, and we will learn one important law that relates stresses and deformations. That is, we will introduce Hooke’s law.

Consider a possible scenario shown in Fig. 1 below. This figure shows a 2D projection of an object that is deformed by force F.

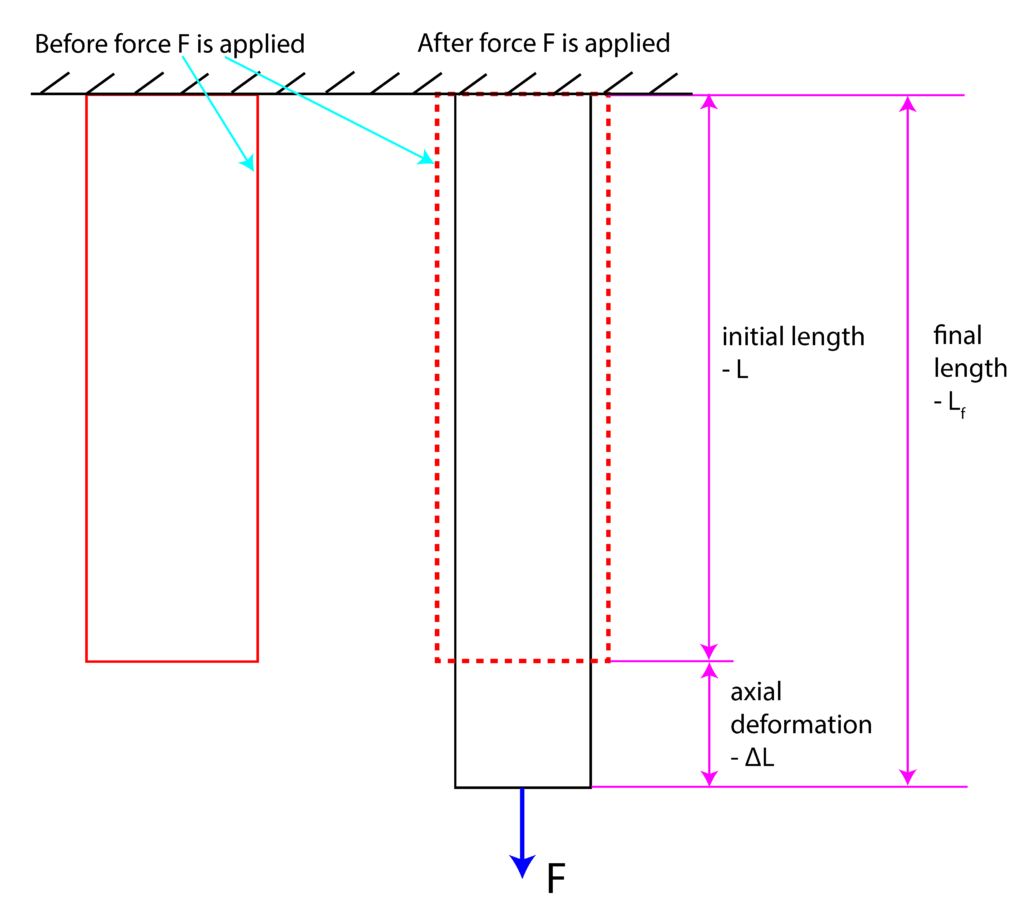
Fig. 1: Deformation of an object under the action of axial force $F$ .

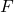The force will cause the object to expand in the axial direction. The initial length of the object is denoted by $L$ . Axial deformation is denoted by $\Delta L$ , and the final length is denoted by $L_{f}$ .

Strain or relative deformation is defined by the following equation

(1) $\begin{align*}\varepsilon =\frac{\Delta L}{L}=\frac{L_{f}-L}{L}\end{align*}$

where $\vareplsion$ is used to denote the strain. The strain is a measure of relative deformation. Why are relative variables introduced in mechanics and physics? Well, imagine that we want to compare the accuracy of two devices for measuring the distance. Imagine that the first device is designed to measure the distance from the Earth to the Moon. Let us assume that this device makes a measurement error of $10$ [m]. Remember that the distance from the Earth to the Moon is approximately equal to 384,400 [km]. That is actually $384400\cdot 10^{3}$ [m]. On the other hand, the second device is designed to measure the distance from one side of a room to another one. Let us assume that the second device makes an error of $2$ [cm] and that the room is square-shaped with the true length of one side of $8$ [m]. Then, we want to pose the following question. Is the second device more accurate than the first one? The answer is simply NO! The reason is that the relative accuracy of the first device is much better than the relative accuracy of the second one. Namely, for the first device, we have

(2) $\begin{align*}\text{relative measurement error} = \frac{10}{ 384400\cdot 10^{3} } = 2.6015 \cdot 10^{-8}\end{align*}$

On the other hand, for the second device, we have

(3) $\begin{align*} \text{relative measurement error} = \frac{0.02}{8} =0.0025 = 2.5\cdot 10^{-3} \end{align*}$

This simple analysis shows that the accuracy of the first device is better than the accuracy of the second one.

The same type of reasoning can be applied to deformation and mechanical systems. For example, the lower road deck of the Verrazzanno Narrows bridge is 12 feet lower in the summer than in the winter, because the steel cables contract or expand as temperature changes! Is this change large or not? Well, we have to take into account the distance from the lower deck to the water. Approximately, this distance is equal to 228 feet. So, the relative deformation is

(4) $\begin{align*}\text{relative deformation}=\frac{12}{228}=0.0526 \approx 5 \text{percent}\end{align*}$

This is a significant change in height of the lower deck. However, the bridge designers have taken into account this when designing the bridge and they made sure that the bridge can safely withstand this deformation.

The second important equation that we will introduce mathematically formulates Hooke’s law. Namely, for the scenario shown in Fig. 1, we have that relatively far away from the action of force $F$ , the normal stress is defined as follows

(5) $\begin{align*}\sigma= \frac{F}{A}\end{align*}$

where $\sigma$ is the stress, and $A$ is the cross-section area of the object. Hooke’s law is defined by the following equation

(6) $\begin{align*}\sigma= E \varepsilon\end{align*}$

where $E$ is the modulus of elasticity (Young’s modulus of elasticity). Note that $E$ can be expressed as follows

(7) $\begin{align*}E=\frac{\sigma}{\varepsilon}\end{align*}$

from where we see that $E$ has the unit of $N/m^{2}$ or $Pa$ (Pascal), that is, $E$ has the same unit as stress. For metals modulus of elasticity is usually in the giga-Pascal range (GPa stands for giga-Pascals), which is in the range of $10^{9}$ $N/m^2$ . For example, $E$ for aluminum alloys is approximately equal to $70$ [GPa]. On the other hand, a typical steel alloy has $E$ approximately equal to $200$ [GPa].

Here it should be emphasized, that Hooke’s law defined by equation (6), is only valid for stresses ranging from $0$ to the value of stress denoted by $\sigma_{P}$ , where $\sigma_{P}$ is the proportional stress limit. Also, it should be emphasized that Hooke’s law is only valid for the elastic deformation of objects. That is, for deformations that are reversible after the force is unloaded.

admin

You might also like

Clear and Concise Explanation of Inheritance in C++

Solve Optimization Problems in Python by Using SciPy Library

Introduction to inverse kinematics of robots