In this mathematics, signal processing, and control engineering tutorial, we provide a clear and concise explanation of the Fourier series. In addition, we solve several examples in order to illustrate how to compute Fourier series. The main goal of this tutorial is to provide a very concise, self-contained, and clear tutorial on the Fourier series, such that students and engineers can quickly grasp the main ideas and obtain a proper understanding of the Fourier series. Also, the idea is to clarify a few misconceptions about the Fourier series and to solve several examples that can help students to better understand the mathematics behind the Fourier series. Finally, we provide Python scripts for computing the coefficients of the Fourier expansion. The YouTube tutorial accompanying this tutorial is given below.
Basics of Fourier Series and Main Formulas
The main idea of the Fourier series is to represent a periodic function as an infinite or finite sum of harmonic signals (![]() and
and ![]() functions). We can also use the Fourier series for periodic extensions of non-periodic functions.
functions). We can also use the Fourier series for periodic extensions of non-periodic functions.
However, before we state the main formulas of the Fourier series, we need to introduce a few important concepts. Consider the figure shown below.
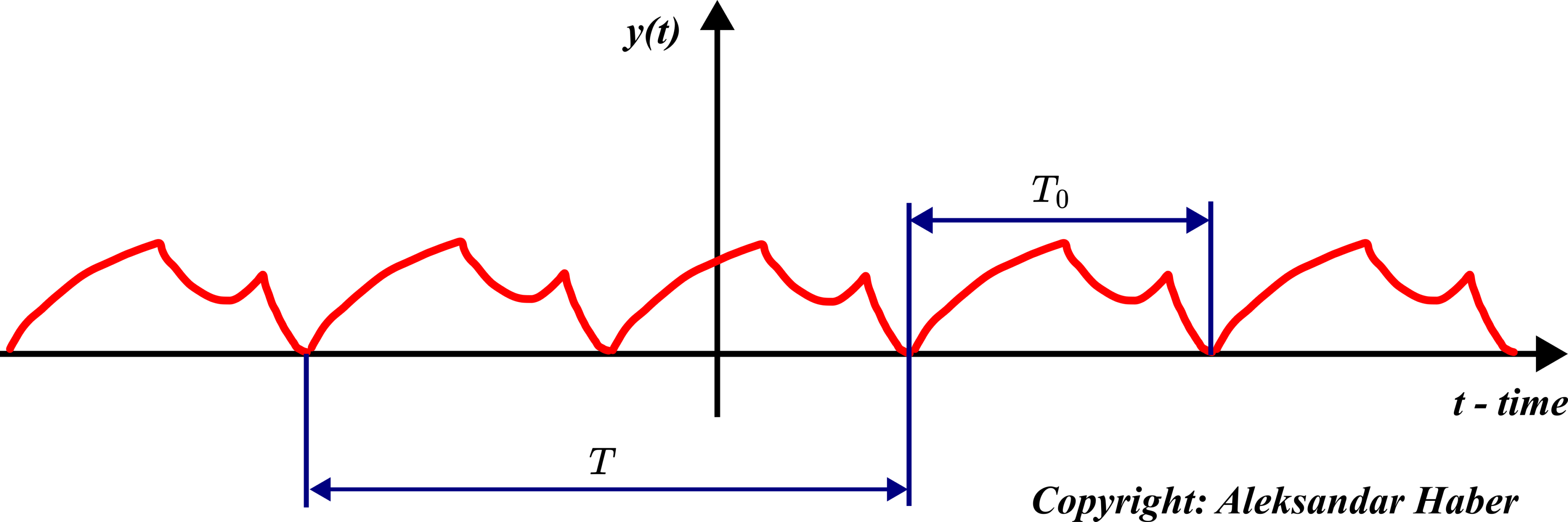
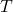 and with the fundamental period of
and with the fundamental period of 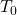 .
.This figure shows a periodic function. Formally speaking, the function ![]() is periodic if and only if there exists a real positive number
is periodic if and only if there exists a real positive number ![]() such that
such that
(1) ![]()
where ![]() is called the period of the function. That is, the periodic function repeats itself after
is called the period of the function. That is, the periodic function repeats itself after ![]() seconds. Now, we are ready to define two very important concepts:
seconds. Now, we are ready to define two very important concepts:
- The fundamental period, denoted by
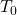 , is the smallest positive real number
, is the smallest positive real number 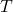 for which the equation (1) is satisfied. The fundamental period is illustrated in Fig. 1. above.
for which the equation (1) is satisfied. The fundamental period is illustrated in Fig. 1. above. - By using the fundamental period, we define the fundamental frequency
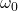 as follows
as follows(2)
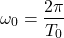
The Fourier series of a periodic function ![]() is defined by the following infinite sum
is defined by the following infinite sum
(3) 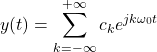
where ![]() is the imaginary unit, and the Fourier series coefficients
is the imaginary unit, and the Fourier series coefficients ![]() are defined as
are defined as
(4) ![]()
The Fourier series form presented above is called the complex form of the Fourier series. Besides this form, there are a number of equivalent mathematical forms that are derived from this form. For signal processing and control engineering, the complex form is the most useful one. In our future tutorials, we will explain other forms.
In the sequel, we provide a more intuitive explanation of the Fourier series. First of all, to better understand the sum (3), let us write first several terms
(5) ![]()
On the other hand, let us recall Euler’s formula for the exponential of the complex number:
(6) ![]()
From this formula, we can see that every complex exponential in (5) or in the general equation (3) can be represented as a sum of ![]() and
and ![]() functions. Consequently, the Fourier series expansion consists of sums of
functions. Consequently, the Fourier series expansion consists of sums of ![]() and
and ![]() functions with different frequencies that are multiples of the fundamental frequency
functions with different frequencies that are multiples of the fundamental frequency ![]() .
.
Now, let us explain what are the DC gain, fundamental component, and harmonics.
- The DC component of the function (signal)
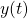 is the Fourier series coefficient
is the Fourier series coefficient 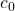 :
:(7)
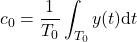
This is simply an average of the function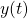 over the fundamental period
over the fundamental period 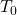 .
. - The elements of the Fourier series expansion obtained for
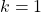 or
or 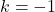 are called the fundamental components or the first harmonic components or simply, first harmonics. That is, the following elements are the fundamental components or first harmonics:
are called the fundamental components or the first harmonic components or simply, first harmonics. That is, the following elements are the fundamental components or first harmonics:(8)
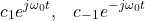
- The components obtained for
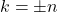 are called the
are called the 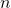 th harmonic components or simply
th harmonic components or simply 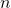 th harmonics. That is, the
th harmonics. That is, the 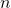 th harmonics are defined by
th harmonics are defined by (9)
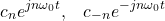
Before we proceed with examples, one very important thing about Fourier series expansion needs to be emphasized. Namely, the coefficients ![]() and
and ![]() are related. From the equation (4), it follows that
are related. From the equation (4), it follows that
(10) ![]()
where ![]() operator is the complex conjugateHere, we give a graphical example of the Fourier series. The goal is to approximate a periodic rectangular wave. In the sequel of this tutorial, we will derive a formula for the Fourier series coefficients of this function. For the time being, we only graphically show the approximation for different values of
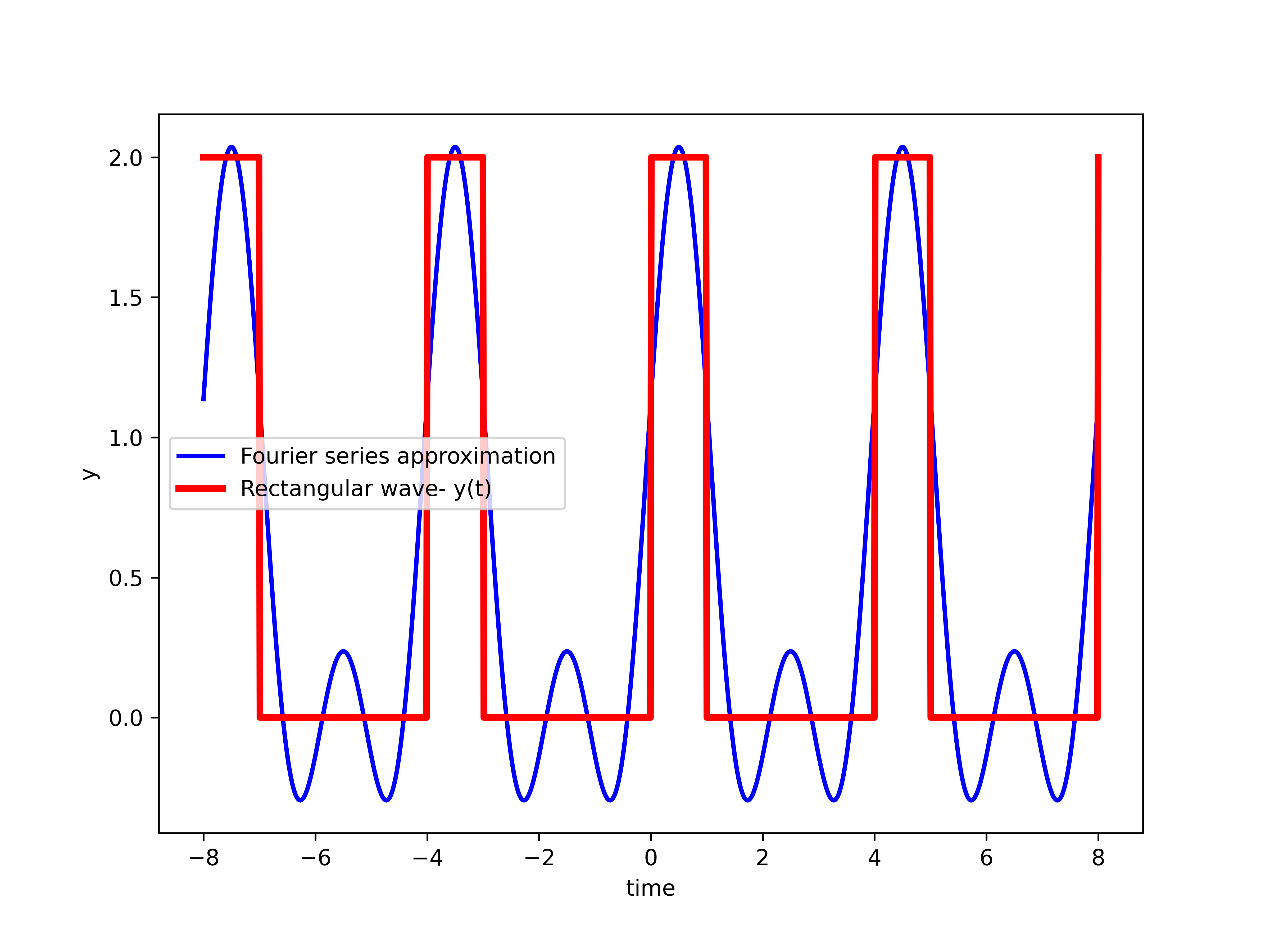
operator is the complex conjugateHere, we give a graphical example of the Fourier series. The goal is to approximate a periodic rectangular wave. In the sequel of this tutorial, we will derive a formula for the Fourier series coefficients of this function. For the time being, we only graphically show the approximation for different values of ![]() . The figure below shows the approximation of the wave for
. The figure below shows the approximation of the wave for ![]() . That is, we only take into account the DC component and the fundamental components. For the fundamental period of
. That is, we only take into account the DC component and the fundamental components. For the fundamental period of ![]() , the approximation is
, the approximation is
(11) ![]()
and figure below shows the graphical representation
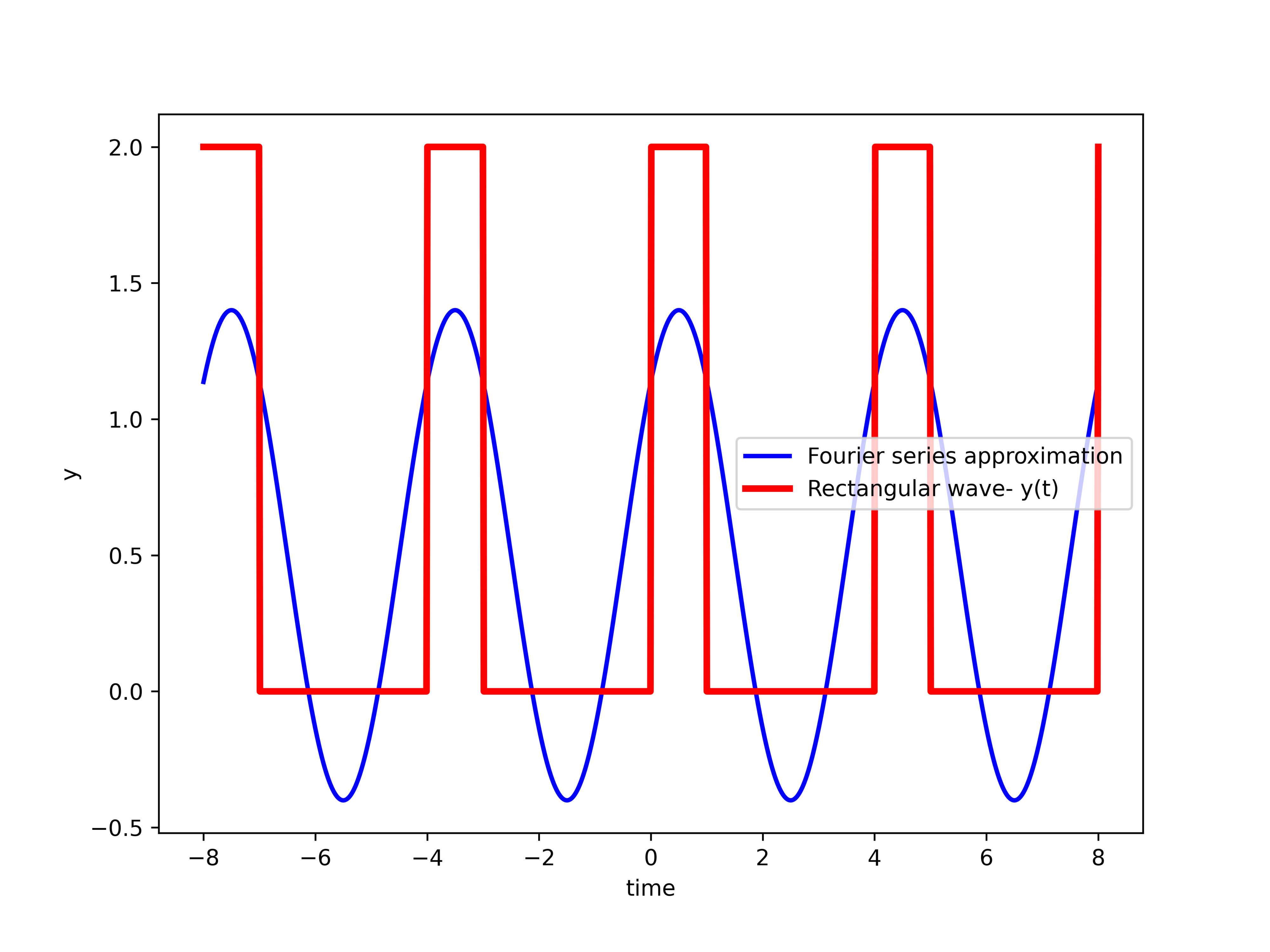
 , and is given by (11).
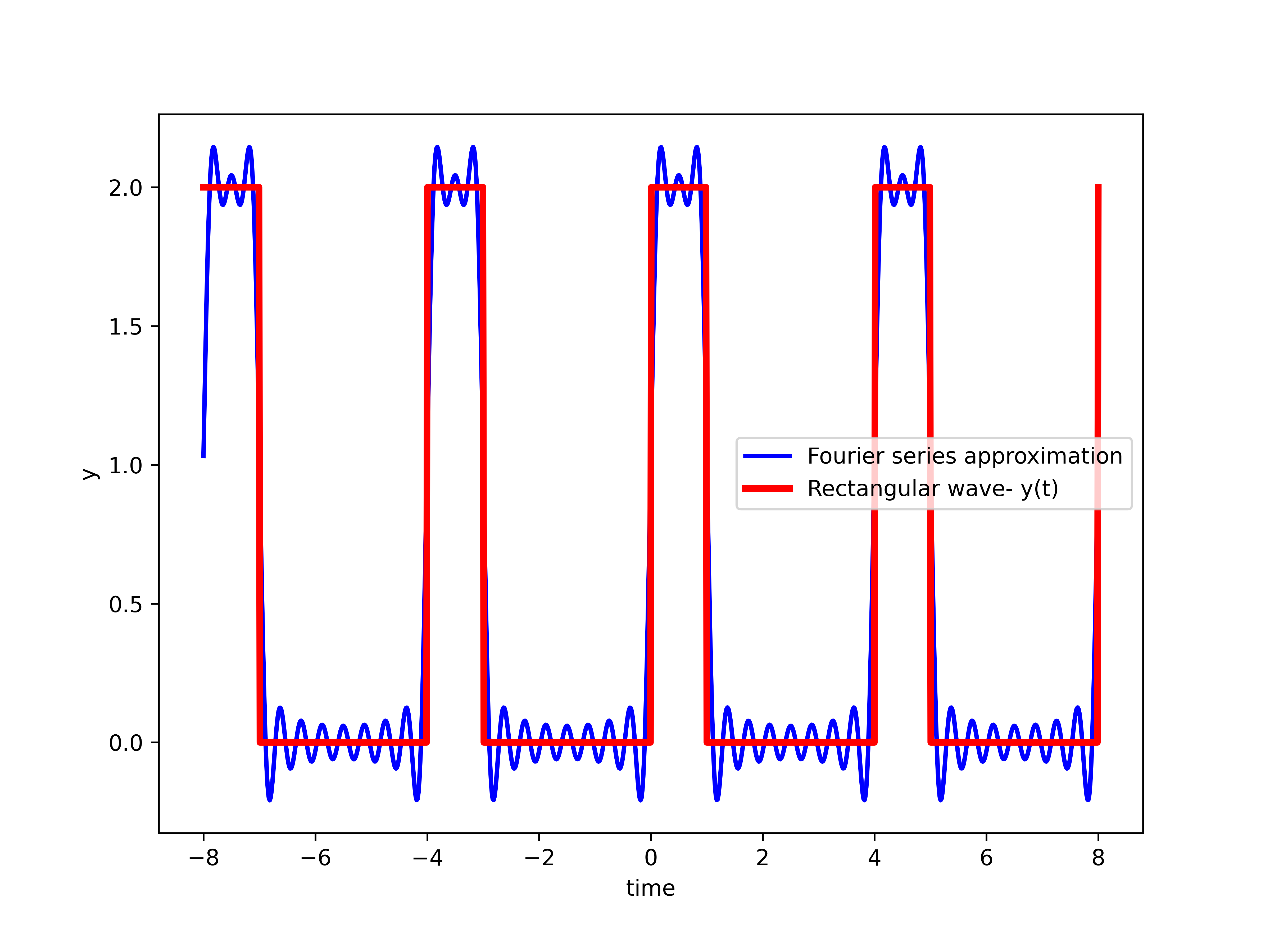
, and is given by (11).For ![]() , we obtain the following approximation
, we obtain the following approximation
(12) 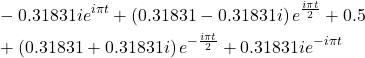
The approximation is shown below.
 , and is given by (12).
, and is given by (12).For ![]() , the approximation is shown in the figure below.
, the approximation is shown in the figure below.
 .
.Example 1: Finite Fourier Series
We consider the following example
(13) ![]()
The goal is to compute the Fourier series expansion of this function.
For ![]() , the function is illustrated in the figure below.
, the function is illustrated in the figure below.
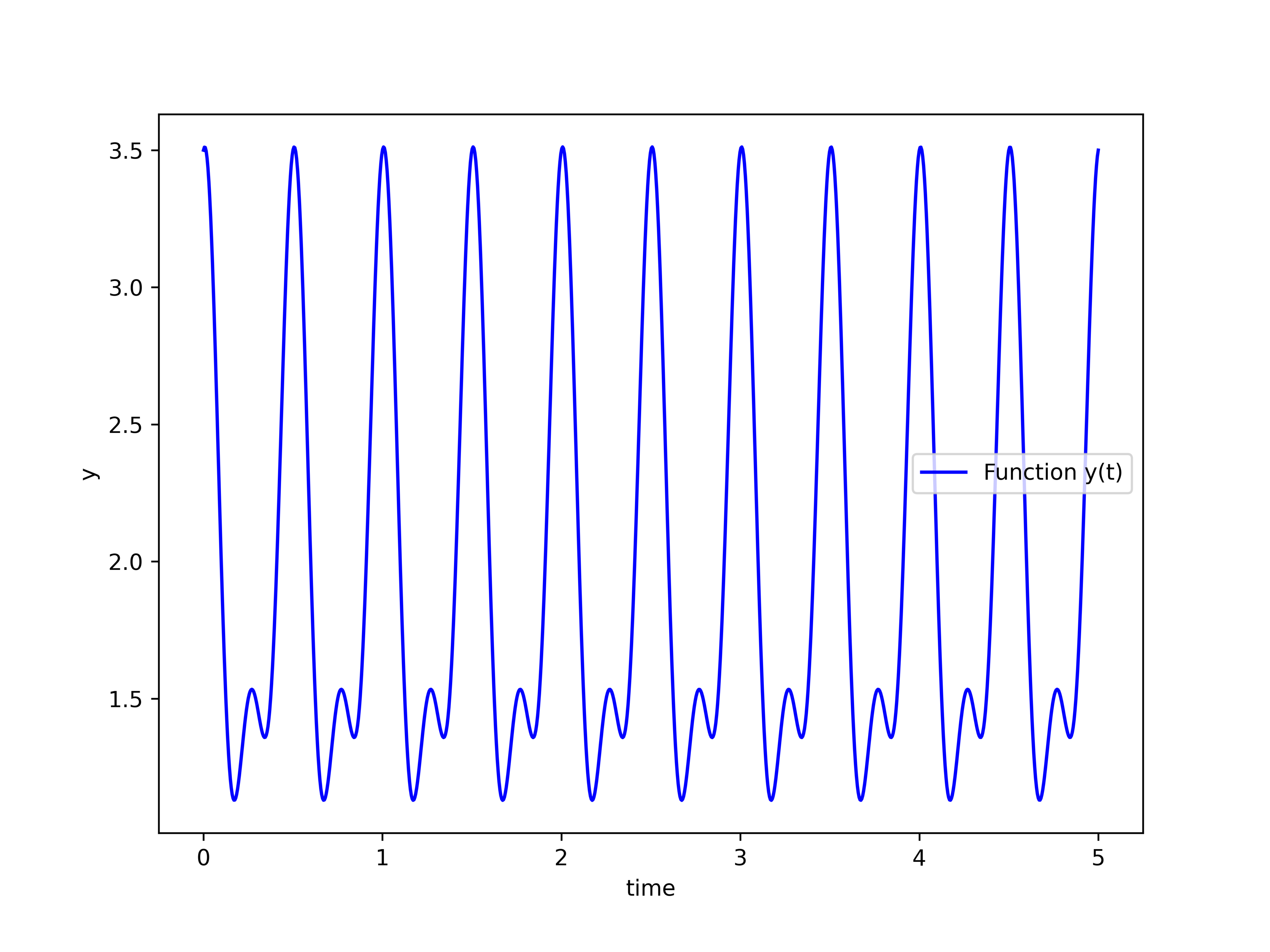
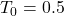
The following Python script is used to generate this graph.
import numpy as np
import matplotlib.pyplot as plt
To=0.5
omega0=2*np.pi/To
timeVector=np.linspace(0,5,1000)
y=2+np.cos(omega0*timeVector)+np.sin(2*omega0*timeVector)+np.cos(2*omega0*timeVector+np.pi/3)
# plot the results
plt.figure(figsize=(8,6))
plt.plot(timeVector, y,'b',label='Function y(t)')
plt.xlabel('time')
plt.ylabel('y')
plt.legend()
plt.savefig('originalFunction.png',dpi=600)
plt.show()
There are two approaches for computing the Fourier series coefficients. The first approach is to use the formula (4). As we will show in the next example, this involves significant effort. However, since this function is a sum of harmonic functions (![]() and
and ![]() functions), there is a direct and less time-consuming approach for calculating the Fourier series. Namely, we can use the following formulas
functions), there is a direct and less time-consuming approach for calculating the Fourier series. Namely, we can use the following formulas
(14) 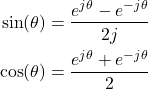
where ![]() is an argument or an angle of
is an argument or an angle of ![]() or
or ![]() function. By substituting every harmonic function in (13), by its exponential form (14), we have
function. By substituting every harmonic function in (13), by its exponential form (14), we have
(15) 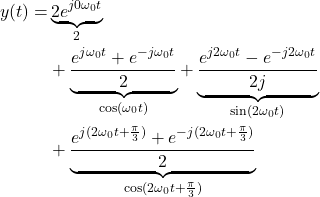
The last equation can be written as follows
(16) 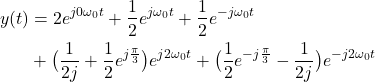
or in the required Fourier series expansion form
(17) ![]()
where the Fourier series coefficients are
(18) 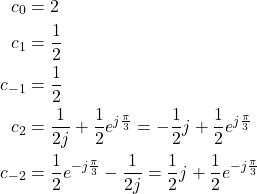
We can also verify that these are correct coefficients by using the following Python script. The Python script given below will be thoroughly explained in out future tutorials.
from sympy import *
t = Symbol('t', real=True)
To=0.5
omega0=2*pi/To
y=2+cos(omega0*t)+sin(2*omega0*t)+cos(2*omega0*t+pi/3)
coeffNumber=[-2, -1, 0, 1, 2]
computedCoefficients=[]
for coeff in coeffNumber:
answer=((1/To)*integrate(y*exp((-coeff*I*omega0*t)),(t, 0, To))).simplify().evalf(6)
computedCoefficients.append(answer)
# double check, the coefficients c2 and c_{-2}
# compare these coefficients with the ones in computedCoefficients
c_2=(-0.5*I+0.5*E**(I*pi/3)).simplify().evalf(6)
c_m2=(0.5*I+0.5*E**(-I*pi/3)).simplify().evalf(6)Example 2: Infinite Fourier Series of Periodic Rectangular Wave (Periodic Pulse Function)
We want to compute the Fourier series expansion of the periodic rectangular wave function shown below.
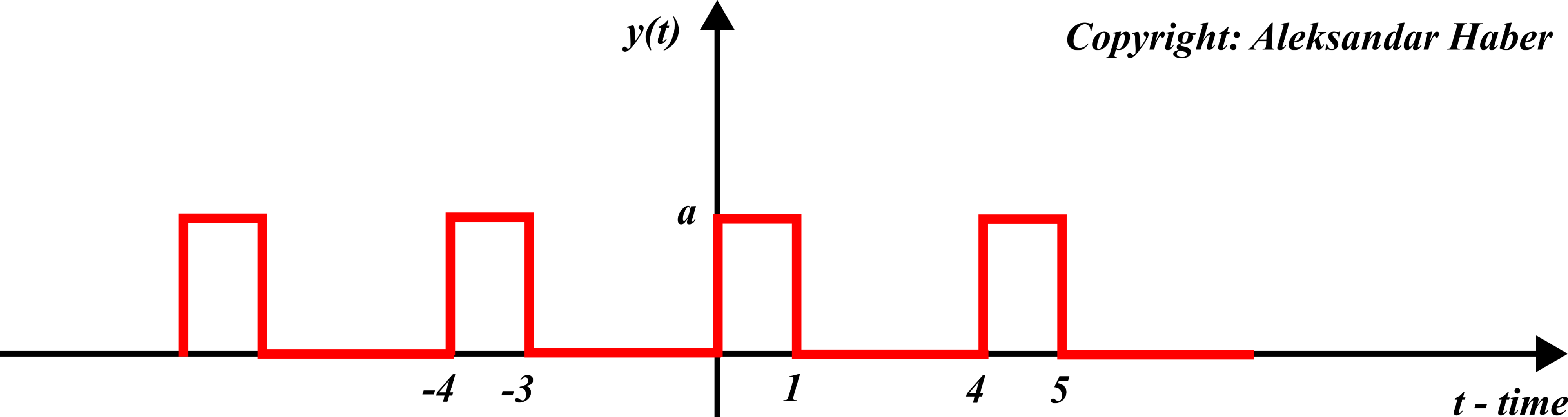
The amplitude of the wave is equal to ![]() . The first step is to identify the fundamental period
. The first step is to identify the fundamental period ![]() . We can see that this function repeats itself every
. We can see that this function repeats itself every ![]() seconds. Consequently, we have
seconds. Consequently, we have ![]() .
.
To compute the Fourier series expansion we need to compute the following integral:
(19) ![]()
Taking into account the shape of the function ![]() shown in Fig. 3, we have
shown in Fig. 3, we have
(20) 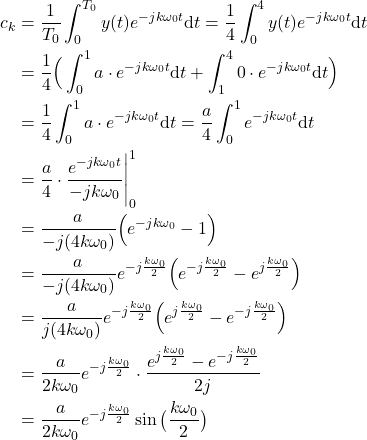
By substituting
(21) ![]()
in the last equation of (20), we have
(22) ![]()
or
(23) ![]()
This is the final expression of the Fourier coefficient. We can also write this expression like this
(24) ![]()
We need to explicitly compute ![]() :
:
(25) ![]()
This is because
(26) ![]()
We can use the following Python script to compute and verify the solution
from sympy import *
t = Symbol('t', real=True)
To=4
omega0=2*pi/To
a=2
# derived formula
k=3
c=(a/(k*pi))*sin(k*pi/4)*E**(-I*k*pi/4)
c=c.simplify().evalf(6)
# use the definition
computedIntegral=((1/To)*integrate(a*exp((-k*I*omega0*t)),(t, 0, 1))).simplify().evalf(6)